なぜ円の面積の求め方は半径×半径×3.14なのか？分かりやすい解説

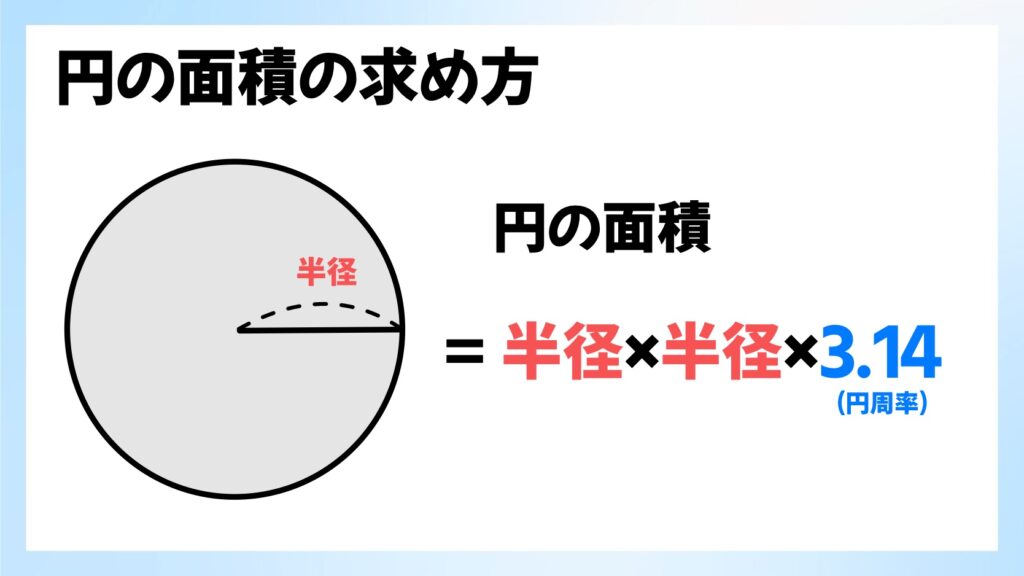
　円の面積は「半径×半径×3.14」という公式で求めることができることは小学生で習います。しかし、なぜ円の面積が「半径×半径×3.14」で求めることができるのかは、あまり教わることはないでしょう。

　この記事を読めば、なぜ円の面積が「半径×半径×3.14」で求めることができるのかという理由がすぐに理解できますよ！

RISU算数（タブレット学習教材）を現役数学教師がレビューしました！

　半径×半径×3.14の理由

　円をケーキのように分ける

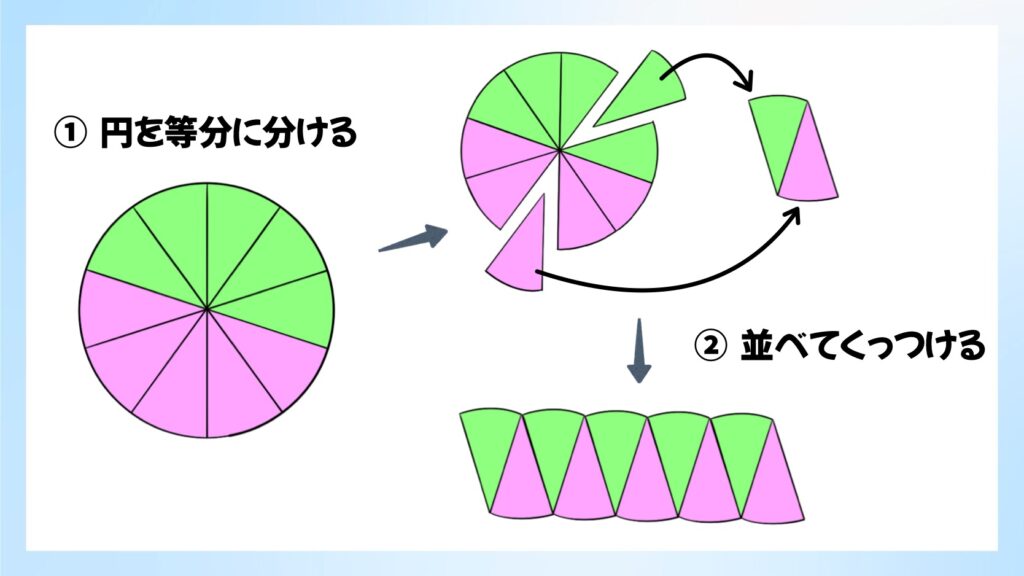
　まず図の①のように円を等分に分けます。ここでは分かりやすいように上半分を緑色に、下半分をピンク色に塗りました。

　このケーキのようなおうぎ形を、②のように互い違いにくっつけて並べていきます。

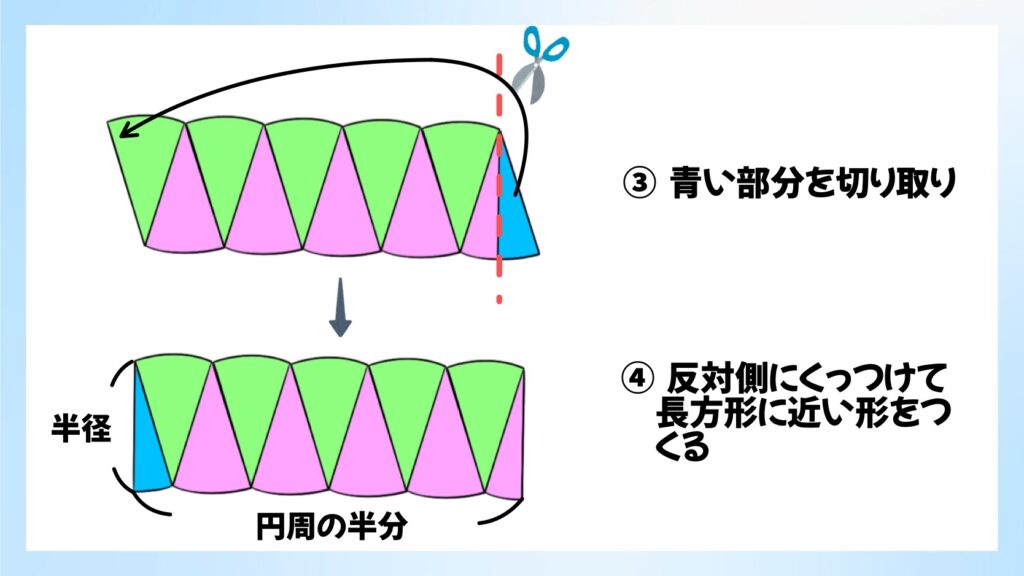
　これを青い部分で切り取り、反対側にくっつけると、長方形に近い形になります。（青い部分を切り取らずに、平行四辺形の形として考えても良い。）

　切り取るおうぎ形を細かくしていくと…

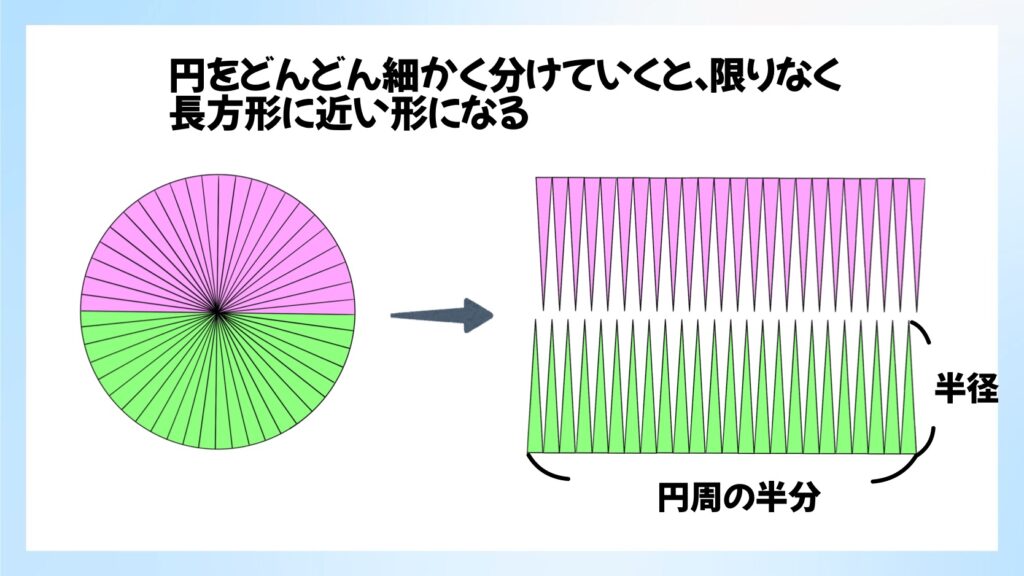
　上のような作業を、円をどんどんと細かく分けていきます。図では48個に分けていますが、もっともっと細かくしていくと、限りなく長方形に近い図形になります。

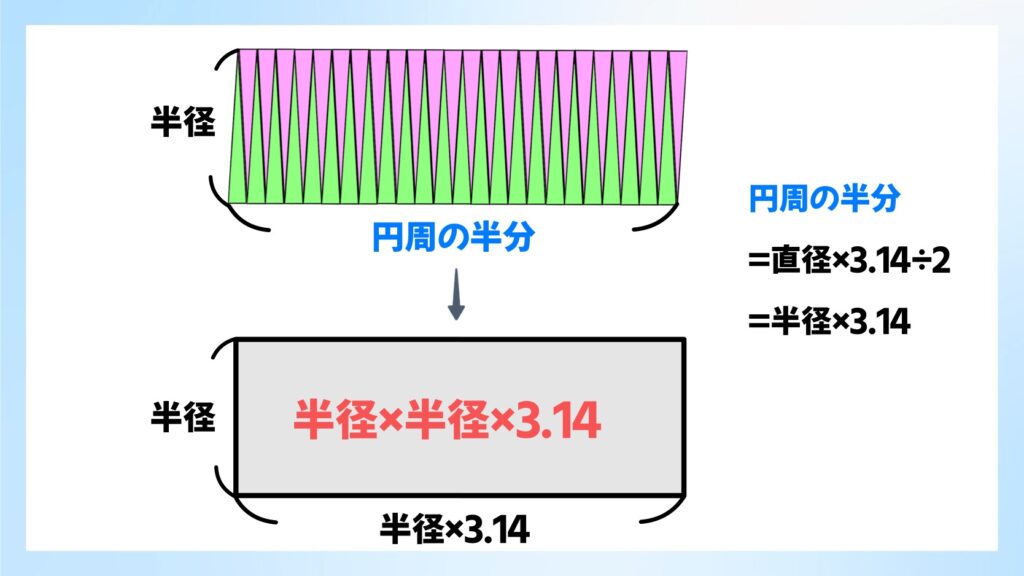
　円からできた長方形の「タテ」の長さは半径と同じ長さで、「ヨコ」の長さは円周の半分の長さになります。

　「円周の半分の長さ」＝「直径×3.14÷２」＝「半径×3.14」となる。

　長方形の面積は「タテ×ヨコ」なので、「半径×半径×3.14」となります。

　まとめ

　数学の中でも特に身近な図形である円。数学を習っていて、円の面積を求める機会は特に多いです。

　円の面積の求め方がなぜ「半径×半径×3.14」なのかを知ることで、円の面積の求め方について更に理解を深めることができるでしょう。