小学校や中学校では、多角形の内角の和を求める公式として180°×(n－2)を学習します。
しかし、
「なぜ180°をかけるの？」
「なぜnから2を引くの？」
と疑問に思ったことはありませんか？
実は、この公式は暗記する必要はありません。三角形の内角の和が180°であることを利用すると、自分で簡単に導き出すことができます。
この記事では、15年間数学を教えてきた私が、多角形の内角の和の公式がなぜ180°×(n－2)になるのかを、図を使いながら分かりやすく解説していきます。
これを見ればあっという間に理解できるよ！
【RISU算数のレビューと口コミ】現役数学教師がタブレット学習教材を使ってみた！
なぜ円周率は３．１４なのか？求め方を分かりやすく紹介！
分数の割り算はなぜひっくり返す？逆数をかける理由を解説！
多角形の内角の和
まず多角形とは角が３つ以上ある平面図形のことを、多角形といいます。そして多角形の内側の角のことを内角といいます。
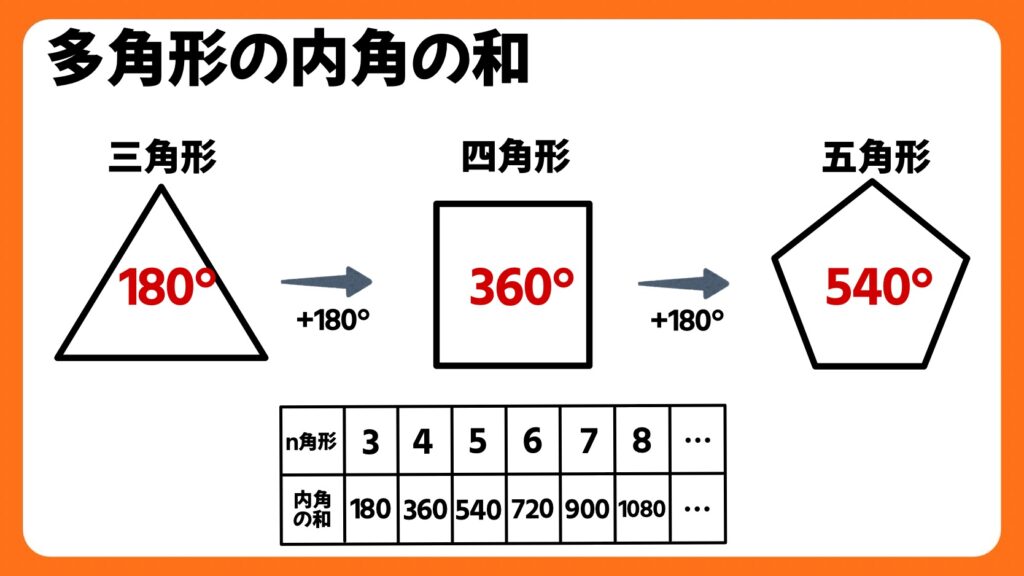
三角形は、それぞれの角を組み合わせると180°、もしくは平行線の錯角と同位角を使うことで180°であることが証明できます。
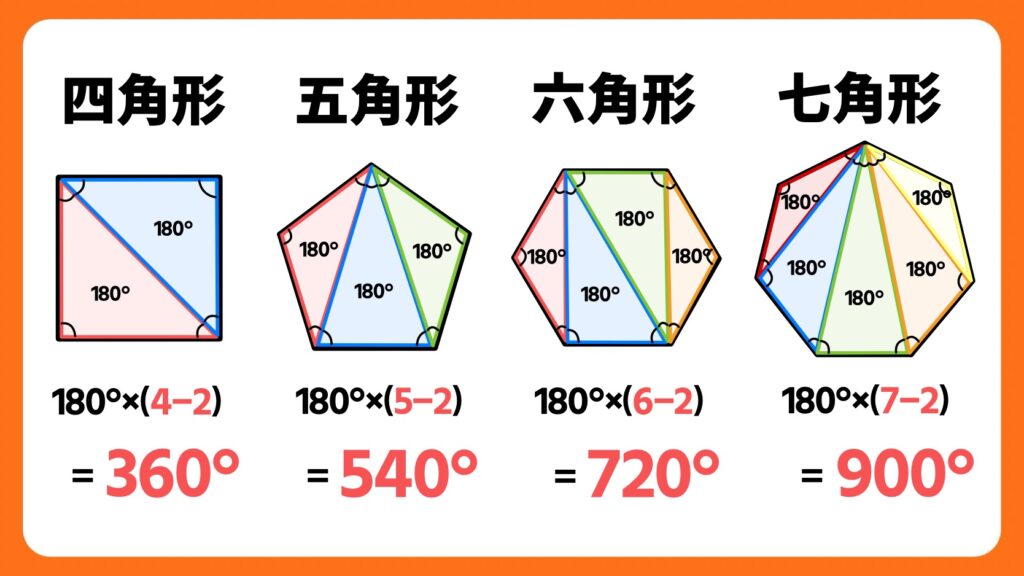
また、四角形や五角形の内角の和は、上の画像のように、角が１つ増えるごとに180°ずつ増えていきます。そう、内角の和には規則性があるのです。
規則性のある内角の和を式に表すと、（角の数－２）×180で求められることが分かります。これをｎを使って表したものが180°×（n－2）という式なのです。
なぜ180° ×（ｎー2）で求められるのか？
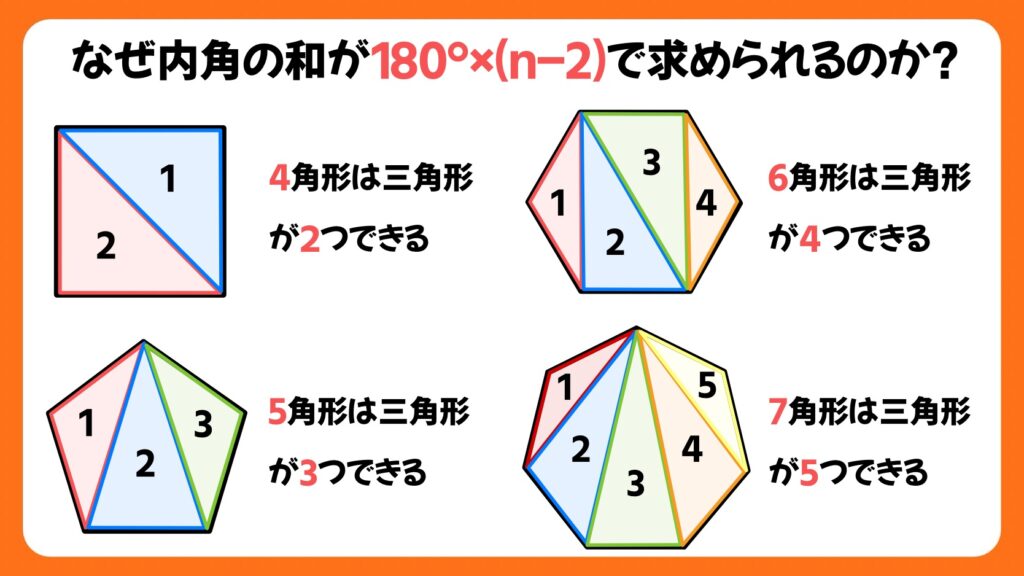
ｎ角形の内角の和がなぜ180° ×（ｎー2）という式で求められるかというと、ｎ角形の中には（ｎー２）個の三角形を作ることができるからです。
上の画像のように、４角形は三角形が２つ、５角形は三角形が３つでき、６角形は三角形が４つでき、７角形は三角形が５つできることが分かります。
三角形の内角の和は180°なので、できる三角形の数×180°ということになります。多角形の角が１つ増えることによって、できる三角形は１つずつ増えていきます。
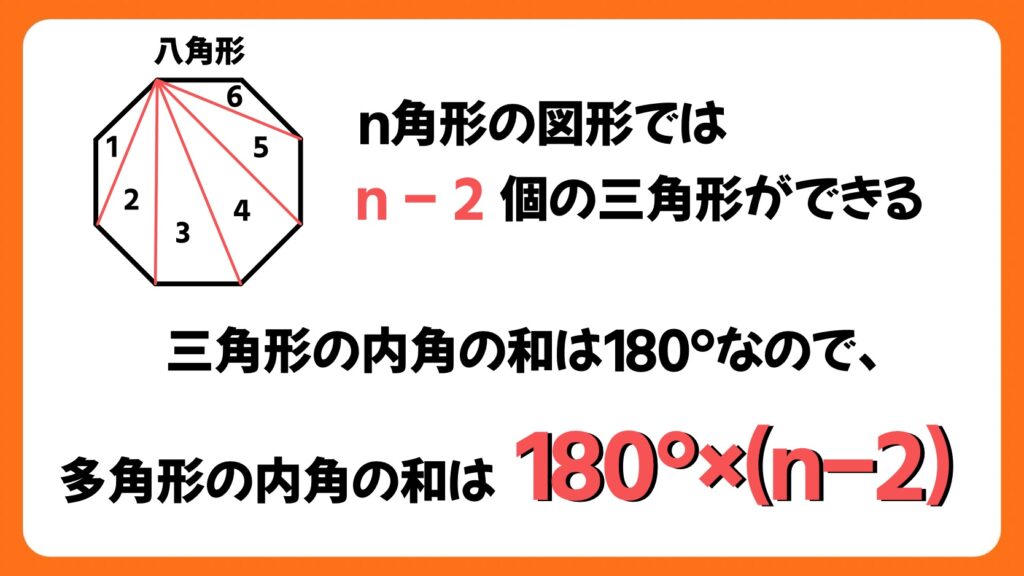
つまり、（ｎー２）個の三角形が作れるｎ角形の内角の和は、180° ×（ｎー2）という式になるということです。
もう一つの考え方
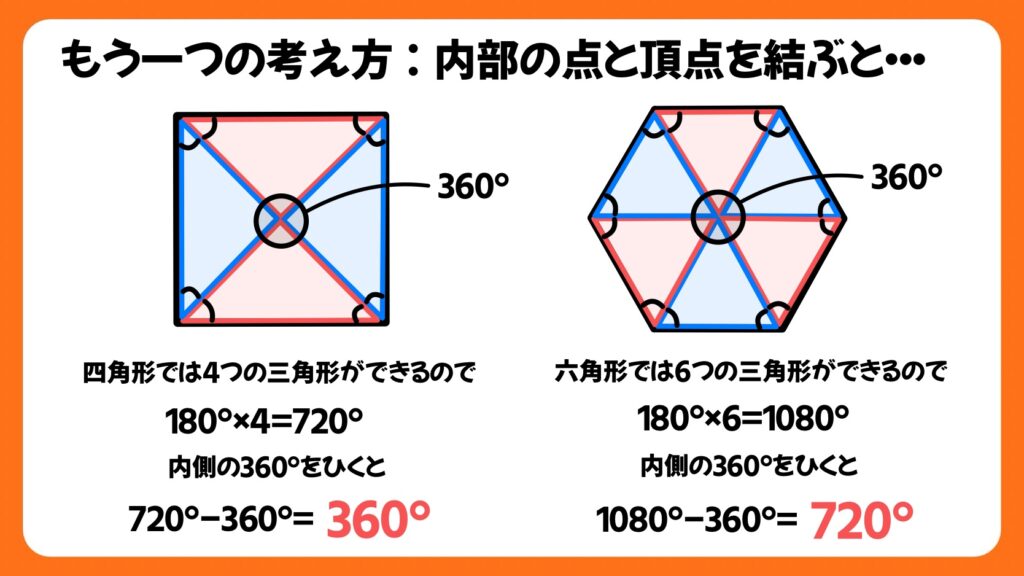
もう一つの考え方を紹介します。まずは多角形の頂点から対角線をひきます。画像の左のように、四角形では三角形が４つでき、全ての角を合わせると、180°×４＝720°となります。
また、画像の右側は六角形の中に三角形が６つでき、その角の合計は180°×６＝1080°となります。
中央の円（360°）は内角の和には関係のない角なので、それぞれの合計の角から360°をひくと、内角の和を求めることができます。
公式を覚えるより理由を理解しよう
算数や数学では、たくさんの公式を学習します。しかし、本当に大切なのは公式を暗記することではなく、「なぜその公式になるのか」を理解することです。
多角形の内角の和は180°×（n－2）という公式で求めることができます。しかし、この式だけを覚えていても、時間が経つと忘れてしまうかもしれません。
一方で、「多角形は三角形に分けて考えることができる」という考え方を理解していれば、公式を忘れてしまっても自分で導き出すことができます。四角形なら三角形が2つ、五角形なら3つ、六角形なら4つできることを考えれば、自然と公式が見えてきます。
算数は答えや公式を覚える教科ではなく、図形や数の仕組みを理解する教科です。特に図形の問題では、「分ける」「並べる」「移動する」といった考え方がとても大切になります。
理由まで理解できるようになると、公式を忘れにくくなるだけでなく、初めて見る問題にも対応できる力が身につきます。
まとめ
いかがだったでしょうか？多角形の中に何個の三角形ができるか？ということを考えれば、内角の和を導くことができることが理解できたと思います。
仮に180° ×（ｎー2）という公式を忘れてしまっても、この仕組みを理解していれば、いつでも自分自身でこの公式を導き出すことができるはずです。
葉っぱ型（レンズ型）の面積の求め方と裏技0.57！算数の不思議を解説！
【最小公倍数と最大公約数の求め方】イラスト付きで分かりやすく解説！
投稿者プロフィール
-
教育×ICTクリエイター｜教育メディア運営
教員15年→2026/3退職 中学数学13年＋小6算数専科2年
Apple Teacher・Kahoot!認定クリエイター
書籍「算数から数学への壁」（エール出版社）
授業で使える算数・数学問題、思考力を育てるクイズ、ICT活用法を発信。
これまでに5種類の兼業を経験し、ストック型副業で月10万円の収益を構築。
電子書籍「論理的思考問題５０」はAmazonベストセラー第７位を獲得。
現在は教育コンテンツ制作、デジタル教材開発、教員の働き方や副業について発信中。
SNS総フォロワー数は約3万人。
