大人が算数を学び直すことには、いくつかの大きなメリットがあります。日常生活や、仕事においても多くのメリットがあるため、算数をを学び直す価値は十分にあります。
この記事では、15年間現役で数学の教師をしている私が選んだ、大人の学び直しに最適な問題を12個紹介したいと思います。大人の今からでも論理的思考を高めることができるので、ぜひチャレンジしてみてください!
算数の学び直しのメリット
- 基本的な数学能力の向上
- 論理的思考力の強化
- 集中力、記憶力の向上
- 子供への教育サポート
- 職業上のスキル、自信の向上

円周率は全て3.14で計算してね!難易度は高いけど、すべて小学生でも解ける問題だよ!
算数オリンピックの問題25選!楽しく考えられるものを厳選!
【空間把握能力を鍛える問題15選】あなたは何問解ける?
円を使ったおもしろい問題20選!小学生でも解ける算数クイズ
問題①
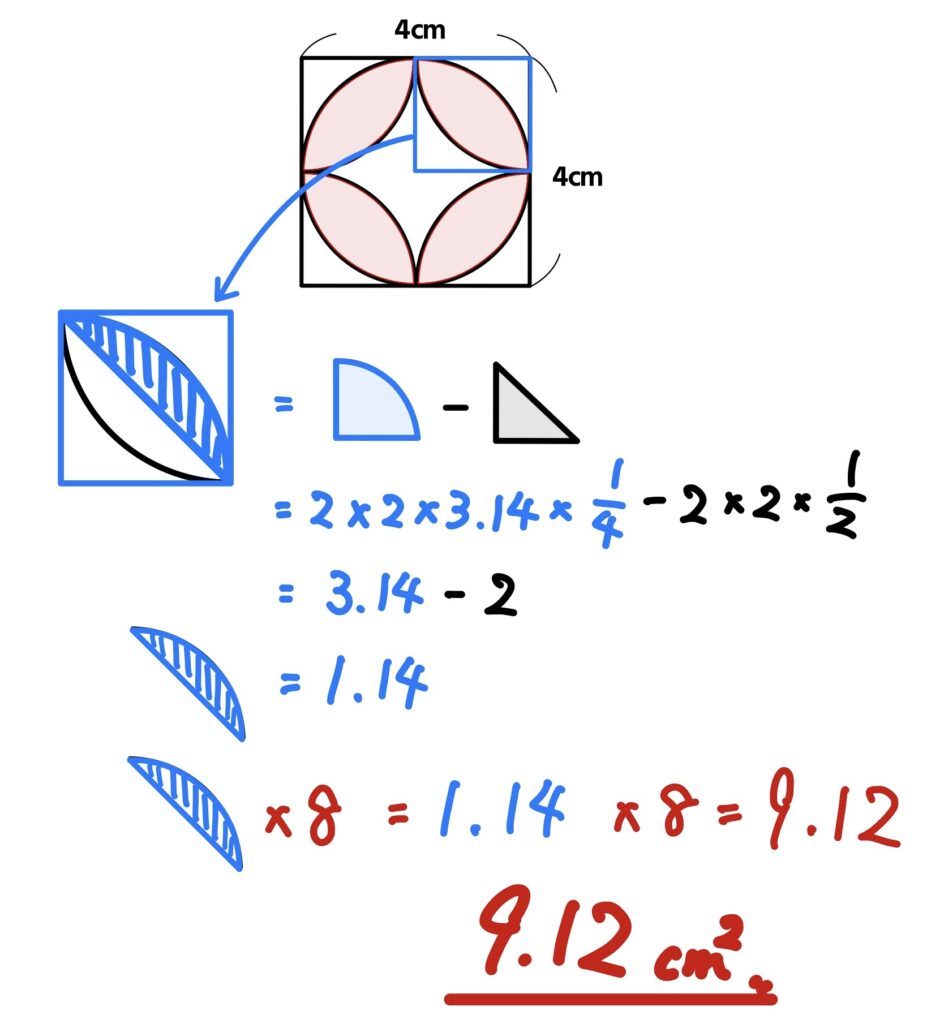
図が1辺が4㎝の正方形の中に円が接していて、その中に半径2㎝のおうぎ形をかいたものです。赤い部分の面積を求めなさい。(円周率は3.14)
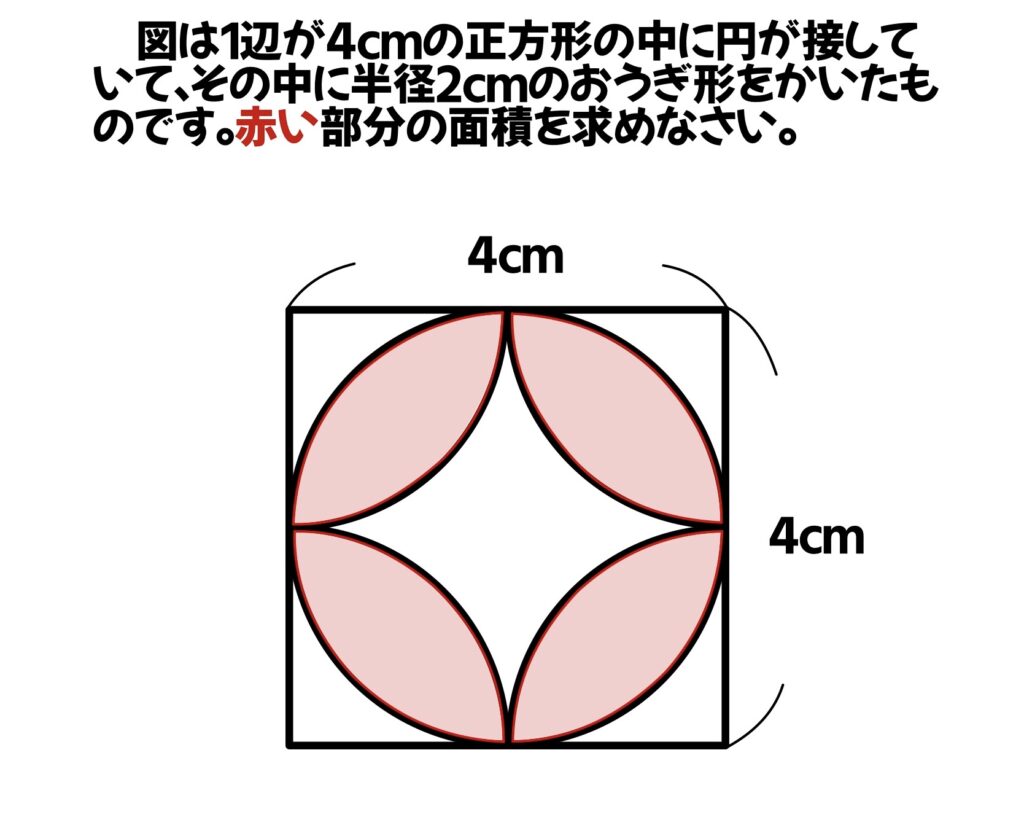

おうぎ形の面積の求め方覚えてますか~?
問題②
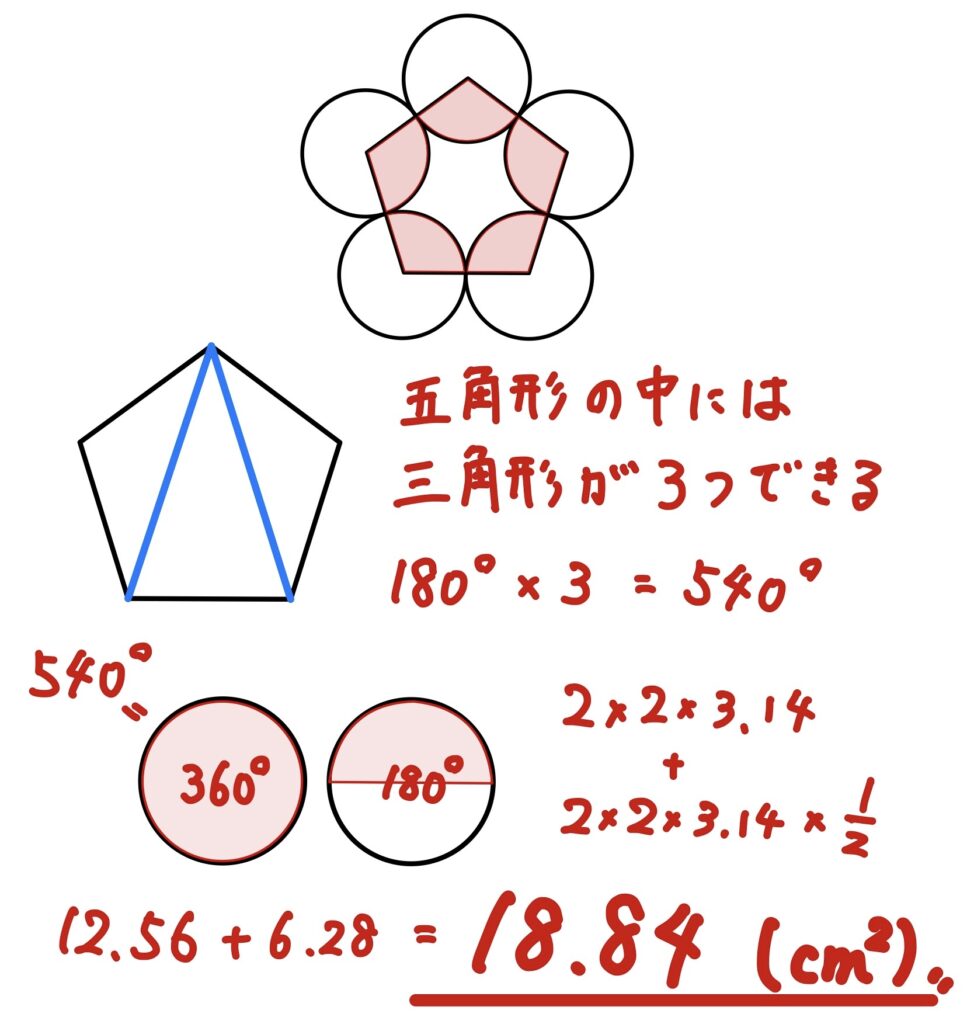
図は半径2㎝の円が5つあり、その中心を結ぶと正五角形になるように接している。赤い部分の面積を求めなさい。(円周率は3.14)


赤い部分の面積は、円何個分?
問題③
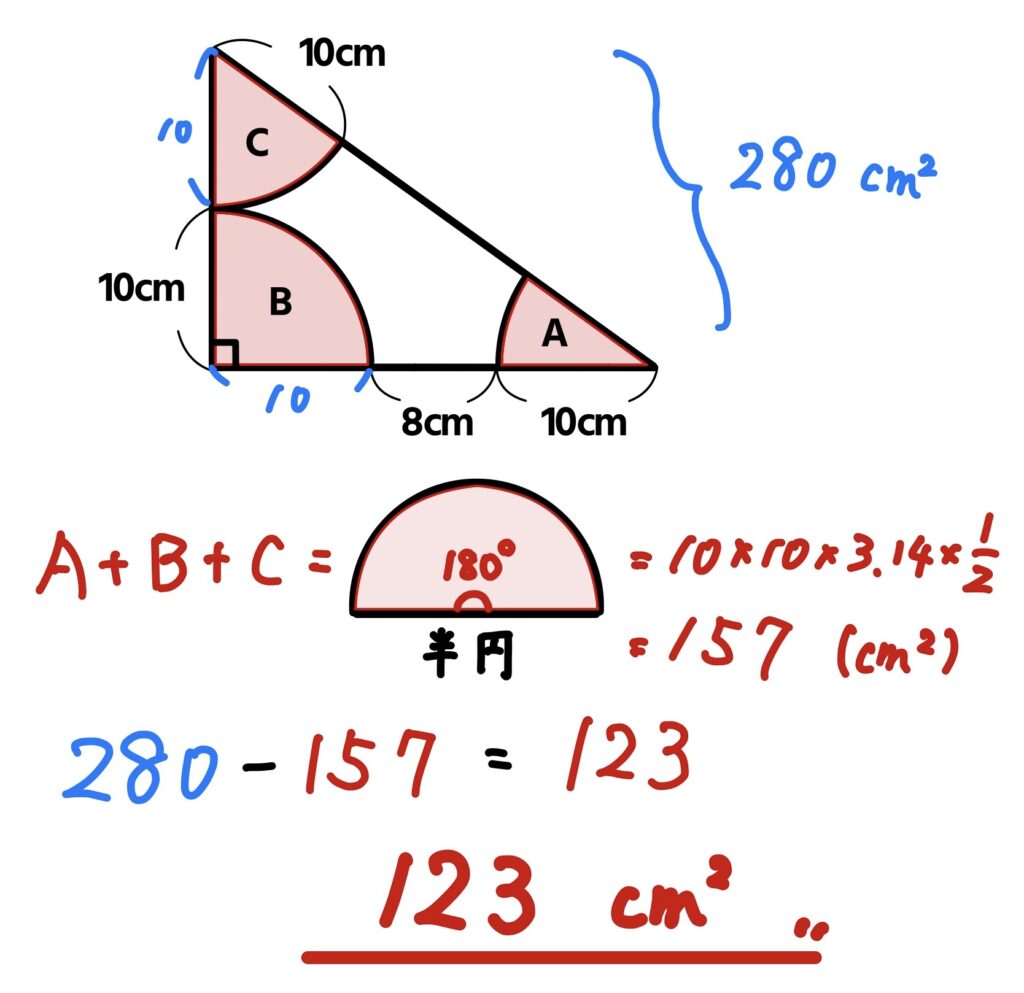
図の直角三角形で、A,B,Cはそれぞれ赤い部分がおうぎ形です。白い部分の面積を求めなさい。(円周率は3.14)
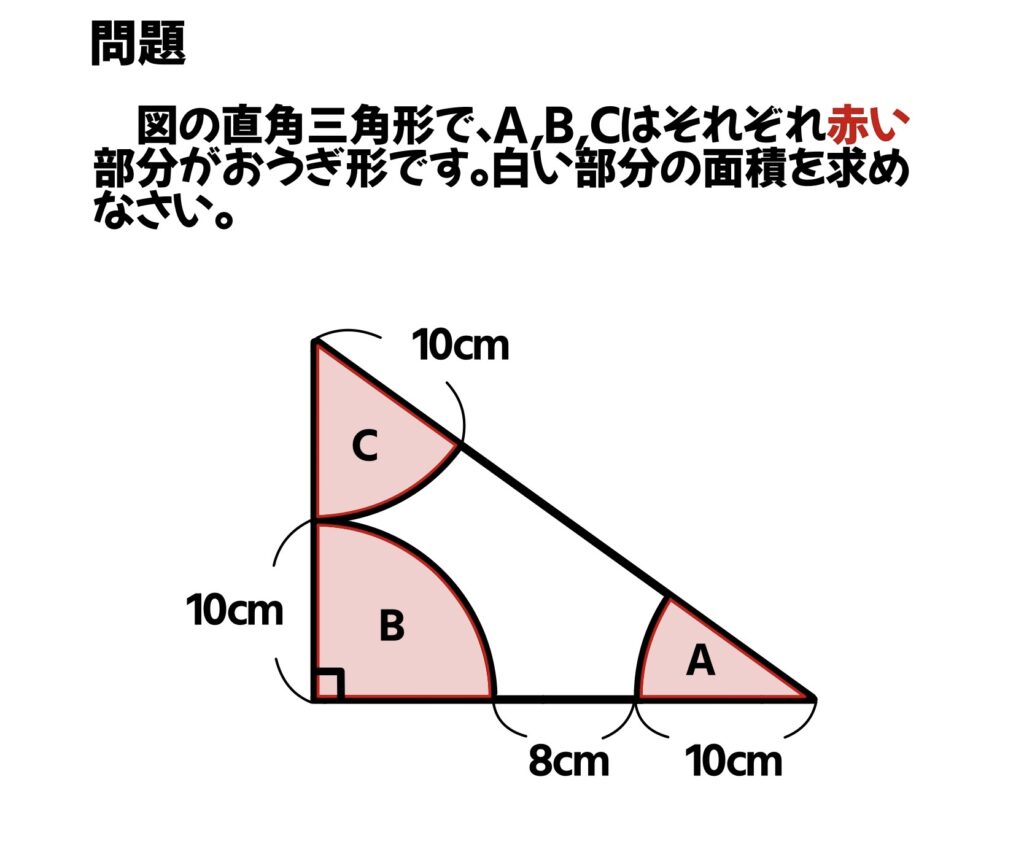

三角形の内角の和は忘れてないよね?
問題④
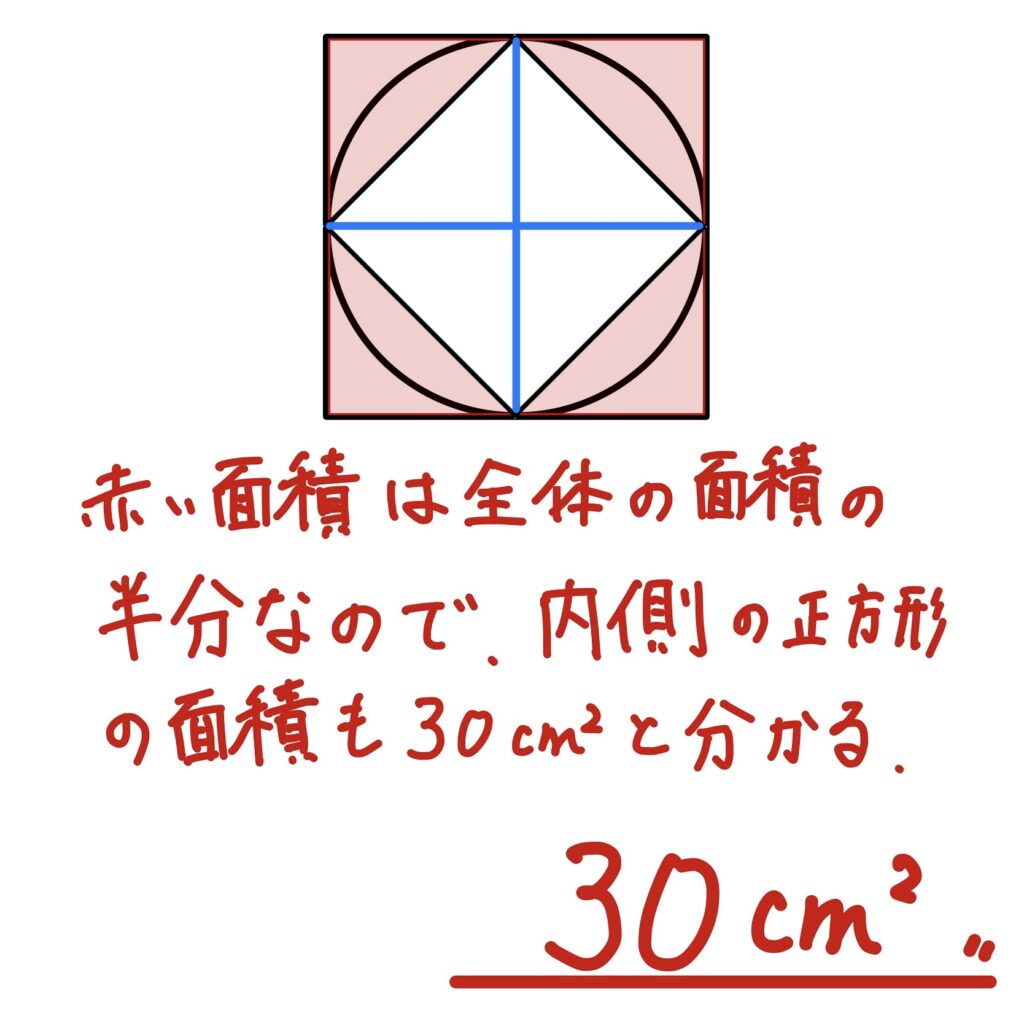
図のように円の外側と内側にそれぞれ正方形が接している。赤い部分の面積が30㎝²のとき、内側の正方形の面積を求めなさい。(円周率は3.14)
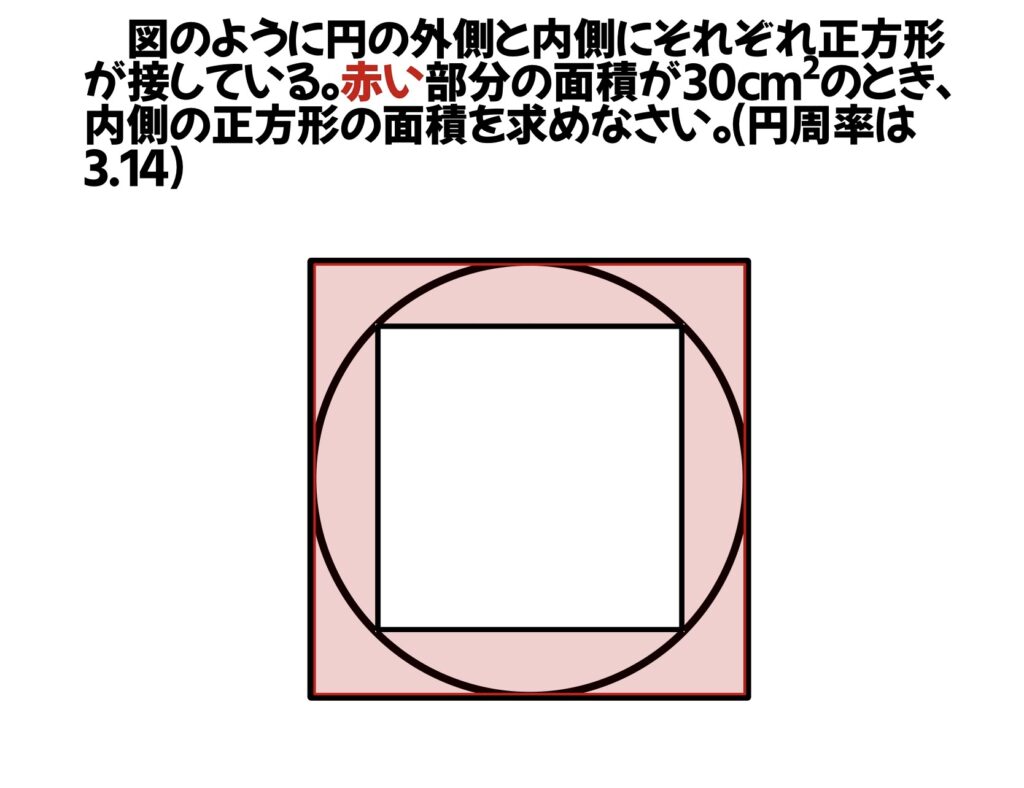

真ん中の正方形をクルッと・・・
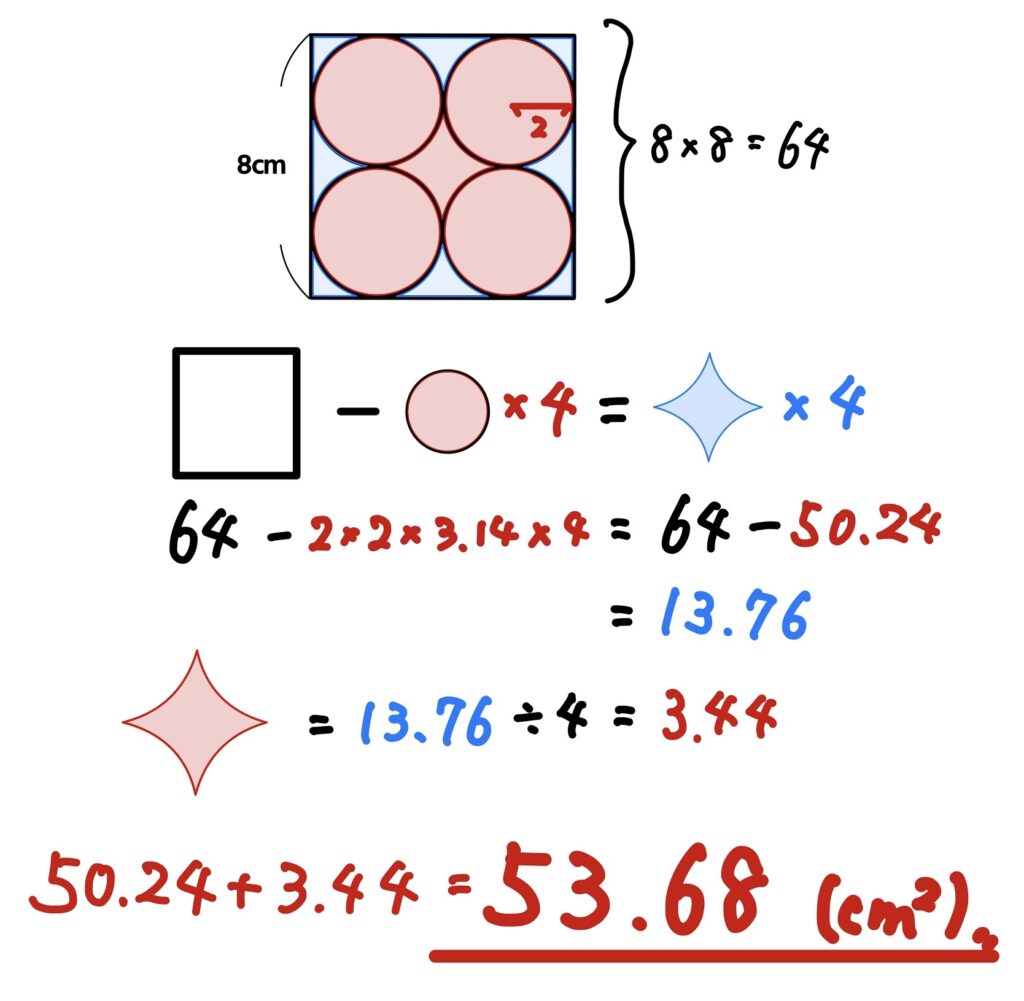
問題⑤
図のように、1辺が8㎝の正方形の中に、半径2㎝の円を4つ並べました。赤い部分の面積を求めなさい。(円周率は3.14)
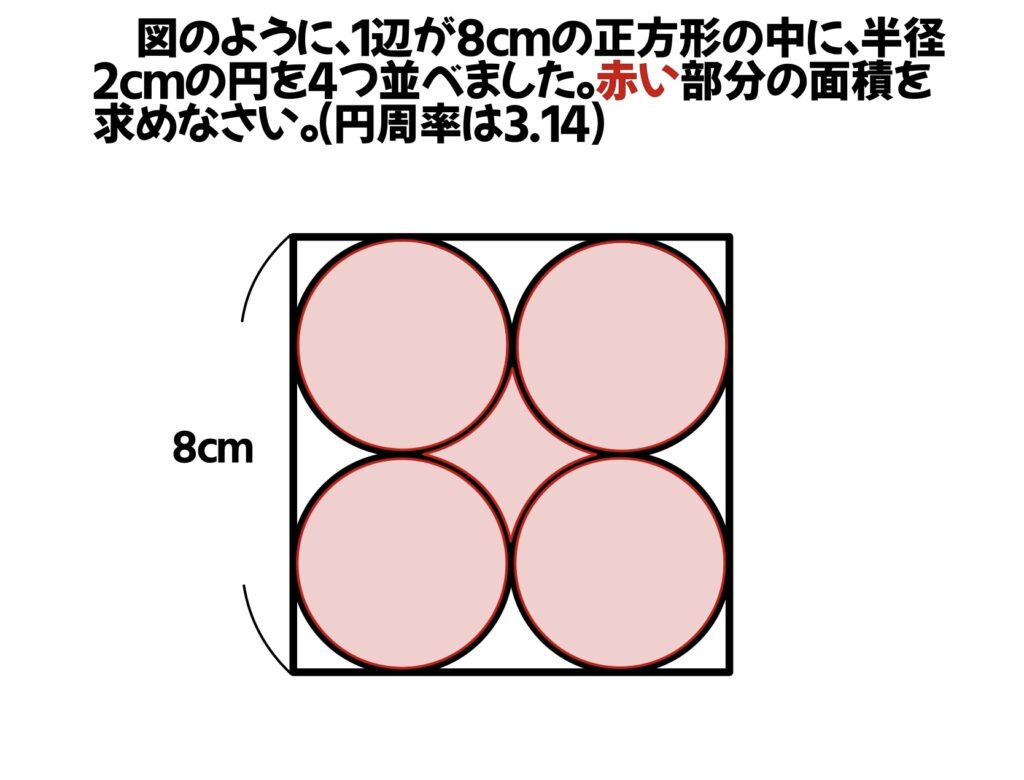

円以外の形と面積がポイント!
問題⑥
図は半径6㎝,中心角60°のおうぎ形です。赤い部分の面積を求めなさい。(円周率は3.14)
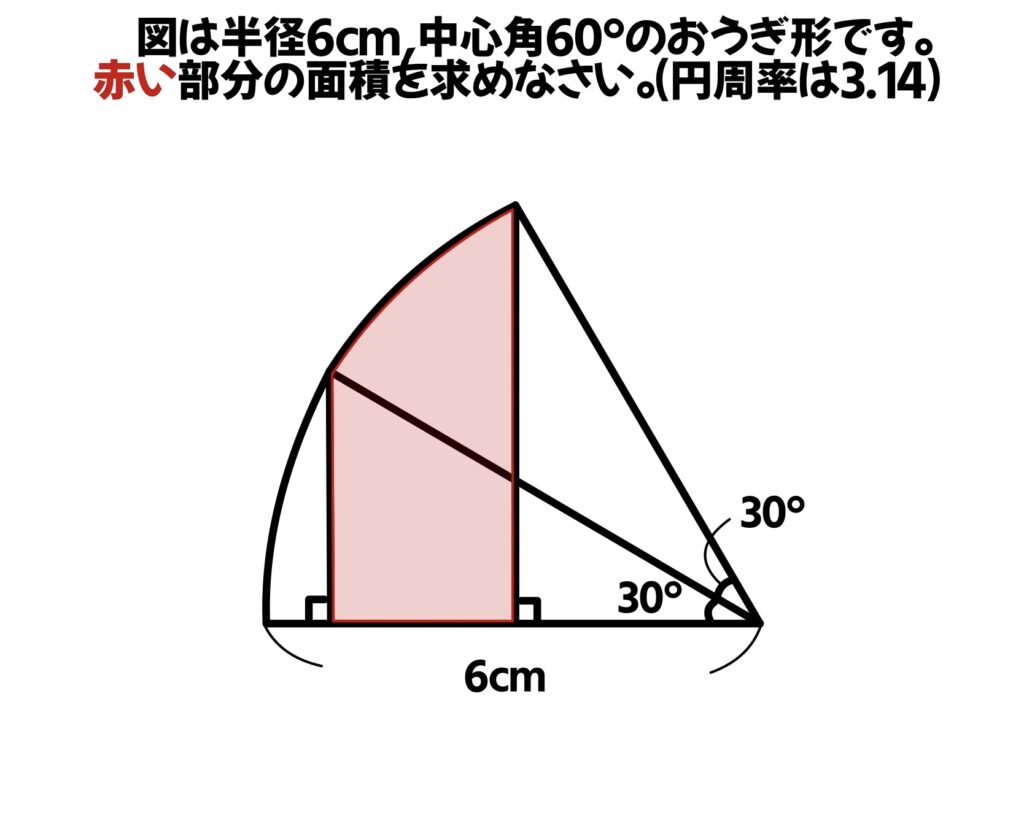

かなりの難問!合同な三角形を考えよう!
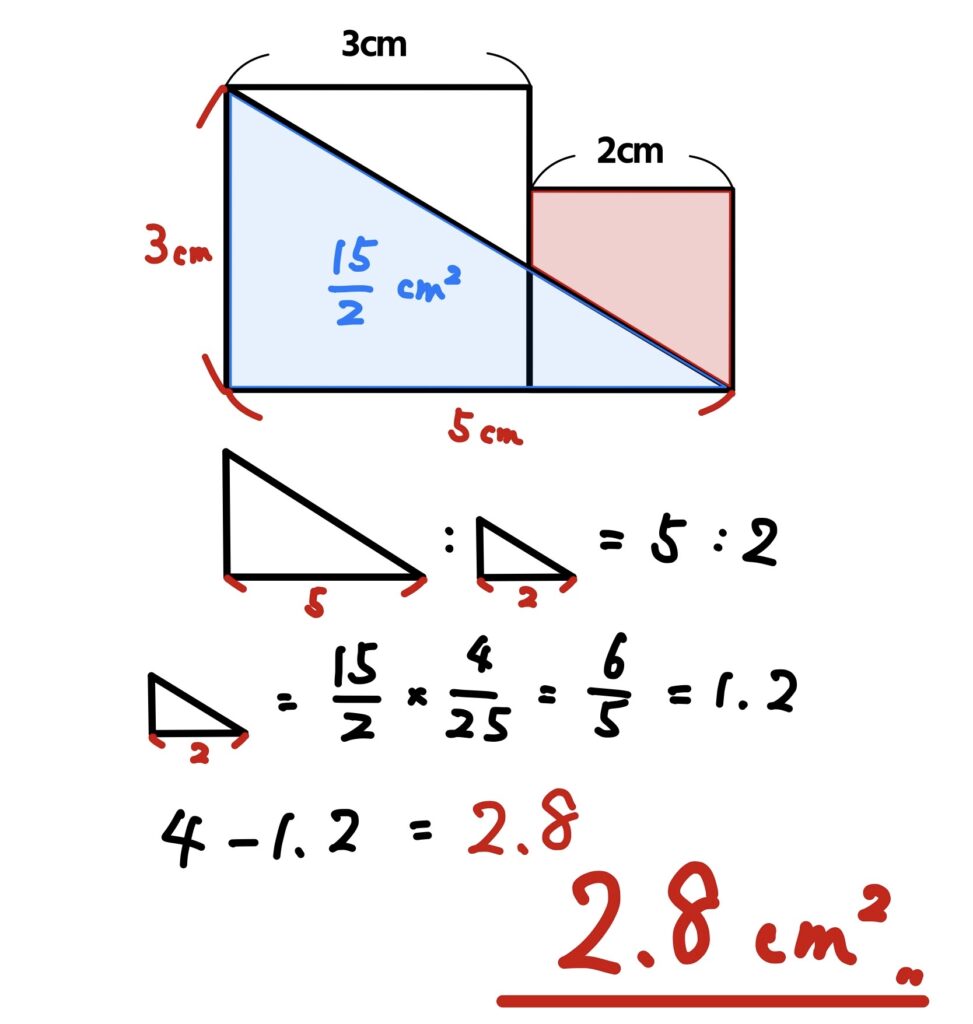
問題⑦
図は1辺が3㎝と2㎝の正方形をつなげたものです。赤い部分の面積を求めなさい。
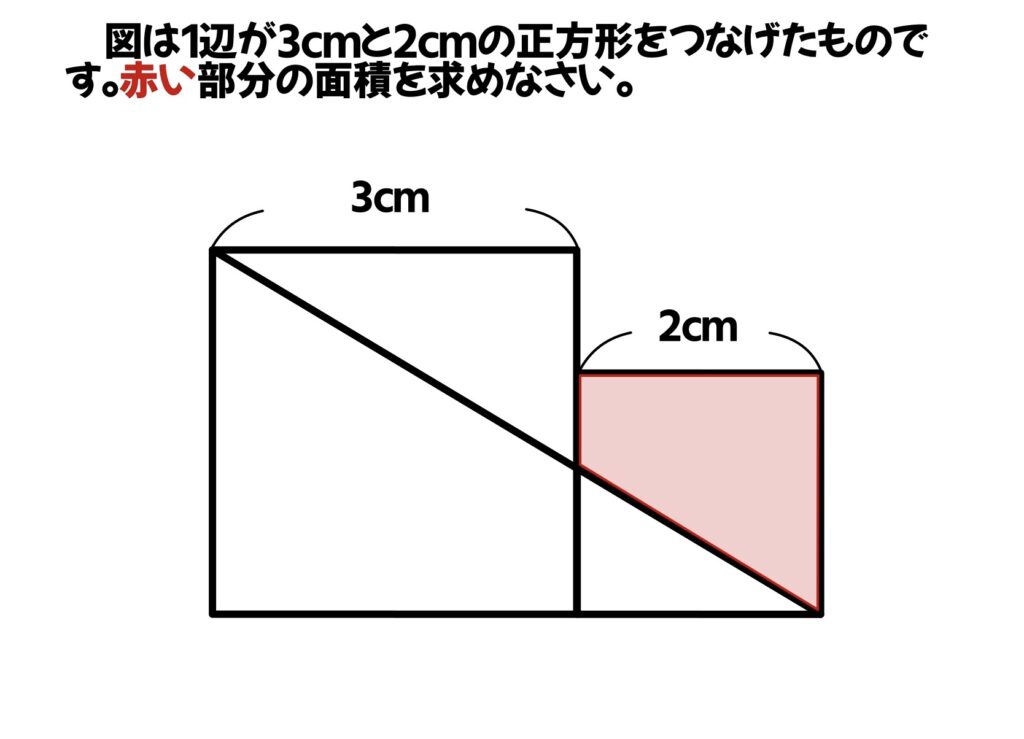

今度は相似な三角形の面積比を思い出そう!
問題⑧
図のような、たて6㎝、横9㎝の長方形の外側を、半径1㎝の円が1周するとき、円が通ったあとの面積を求めなさい。(円周率は3.14)
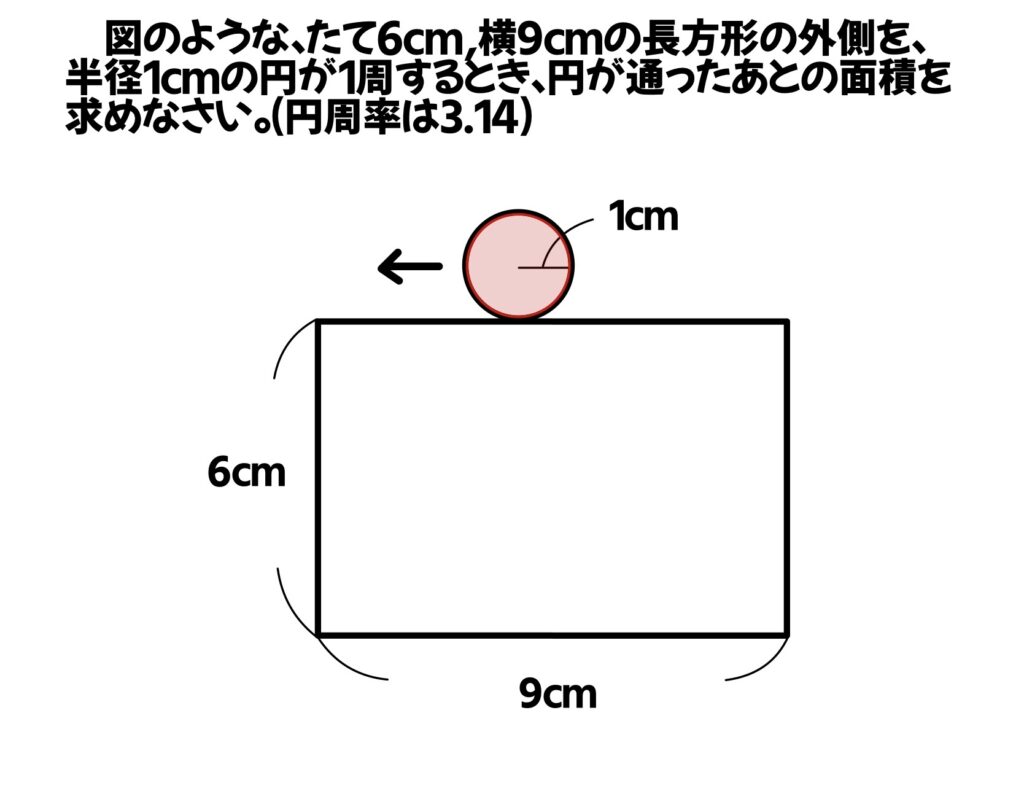

円が1周した時の角を部分をイメージしよう!
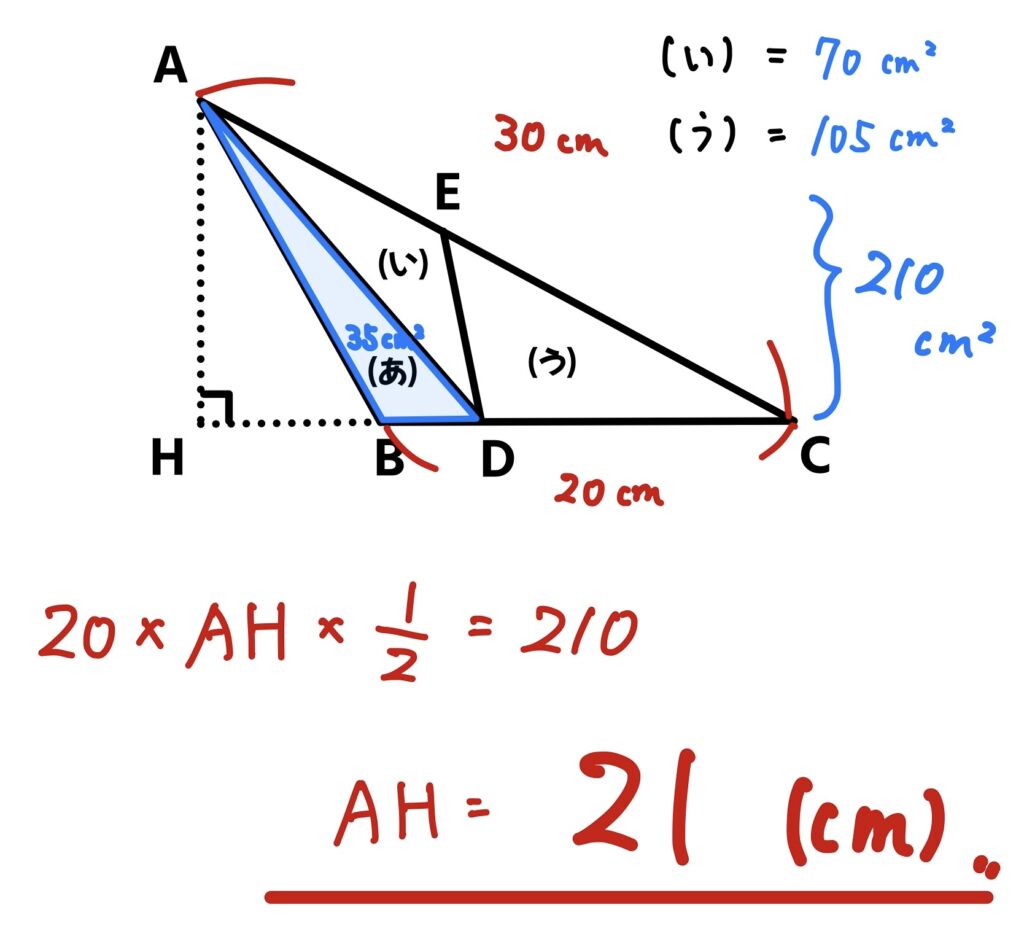
問題⑨
図はACが30㎝,BCが20㎝の三角形で、三角形(あ):(い):(う)の面積の比は1:2:3です。(あ)の面積が35㎝²のとき、AHの長さを求めなさい。
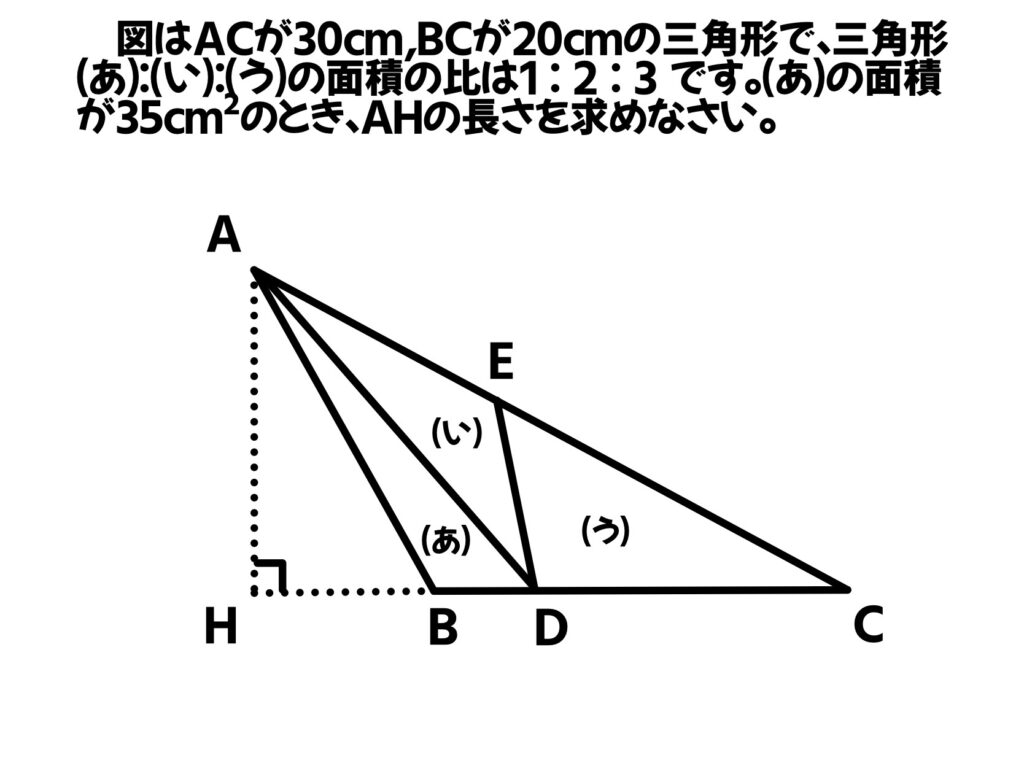

全体の面積を求めれば意外と簡単かも
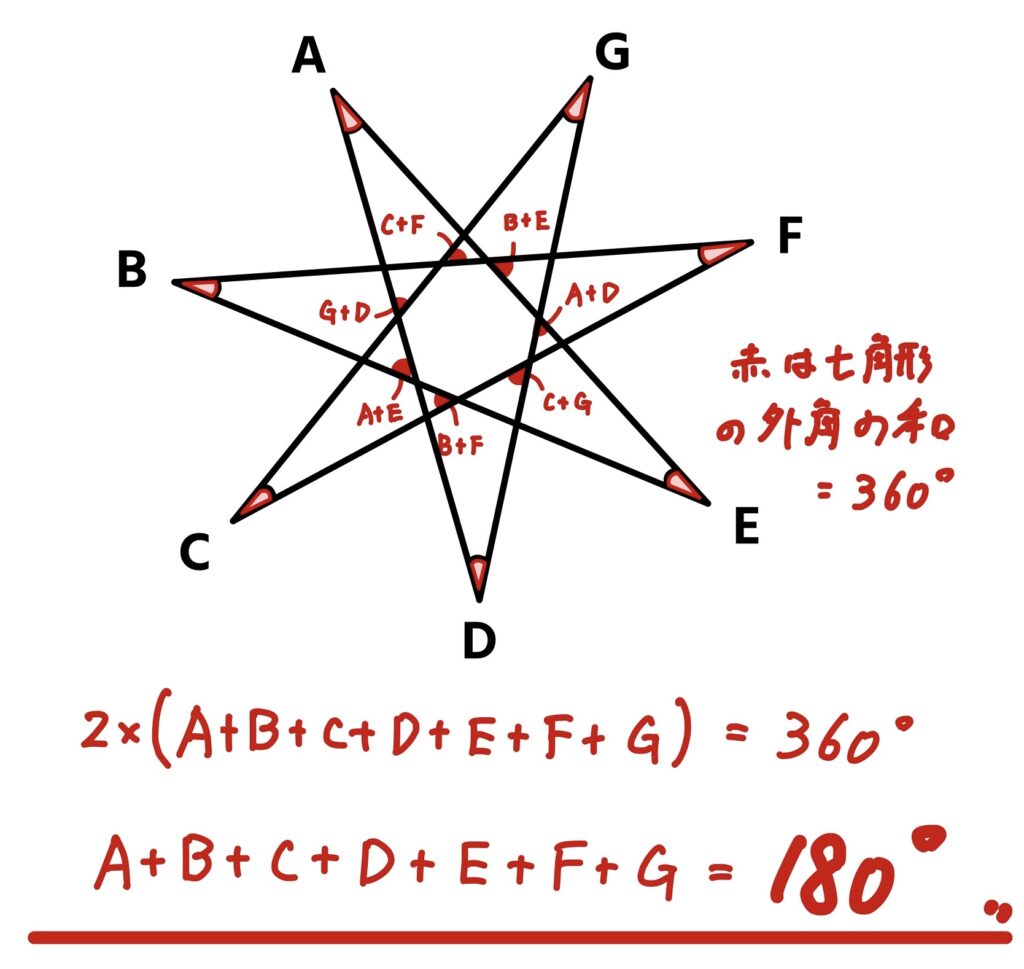
問題⑩
下の図の角度A,B,C,D,E,F,Gの和を求めなさい。
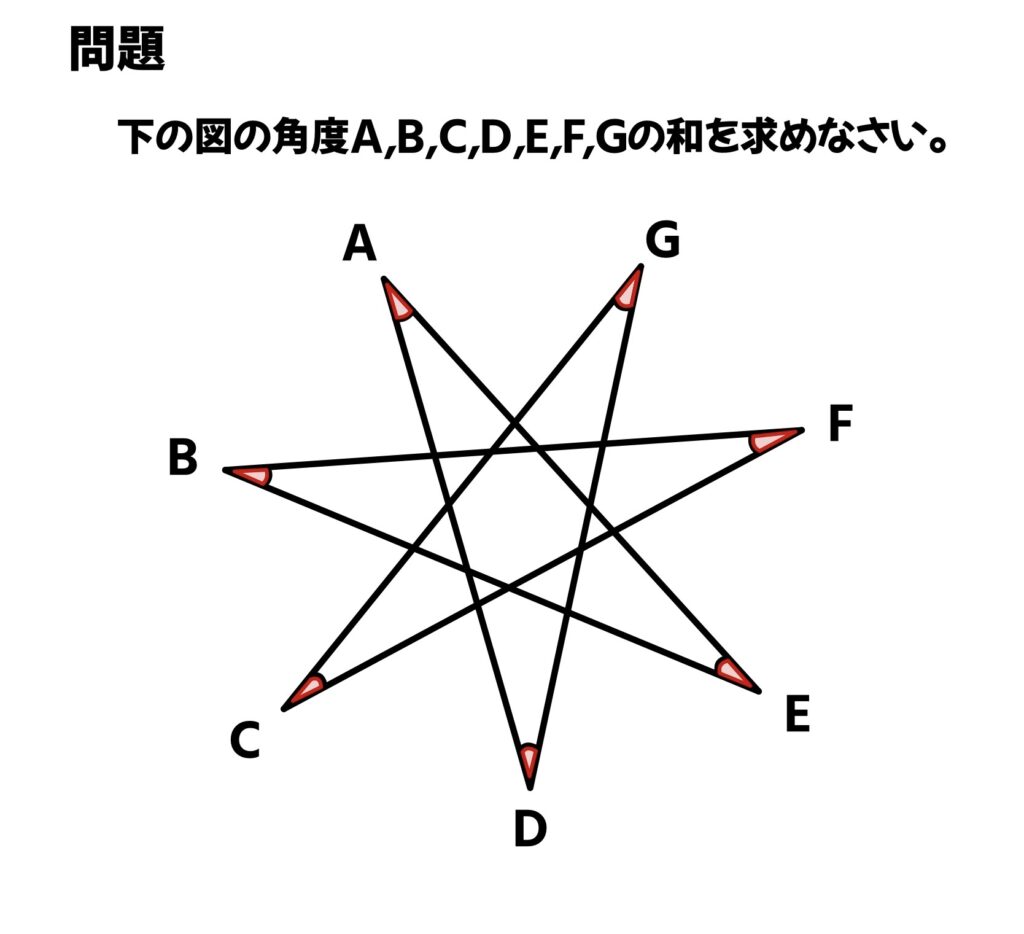

いろんな解き方があるよ!真ん中の七角形に注目!
問題⑪
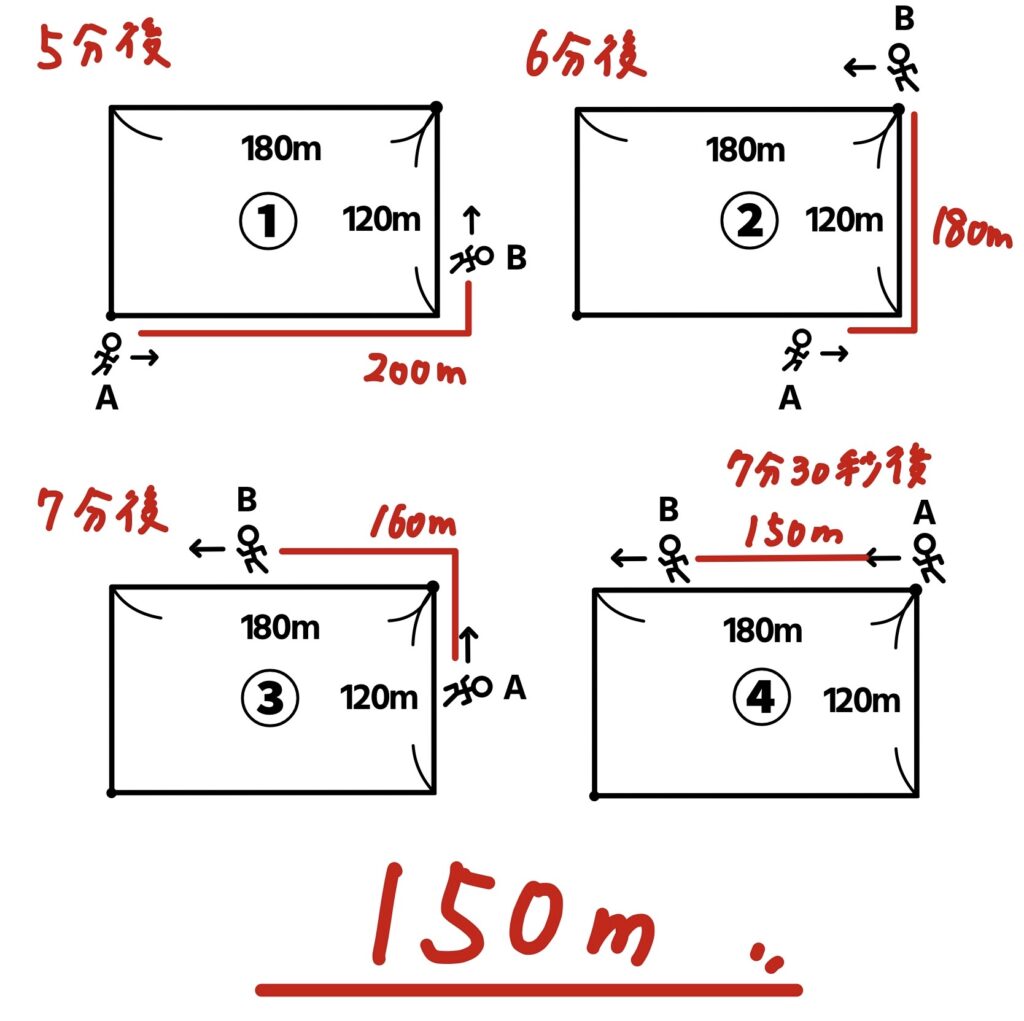
図のような長方形の建物の周りをAが毎分120m,Bが毎分100mの速さで同時に図の位置から走ります。初めてAがBを見つけたとき、AとBは何m離れていますか。
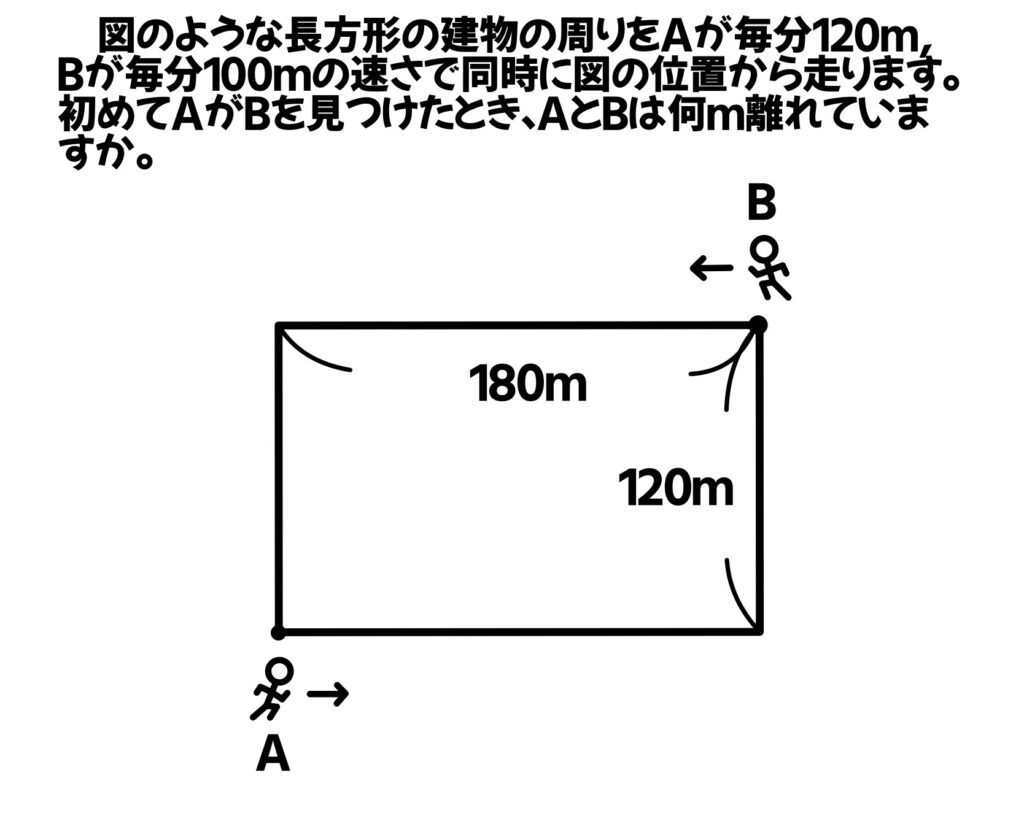

Aが角を曲がった瞬間に、Bが見えたときの距離だよ!
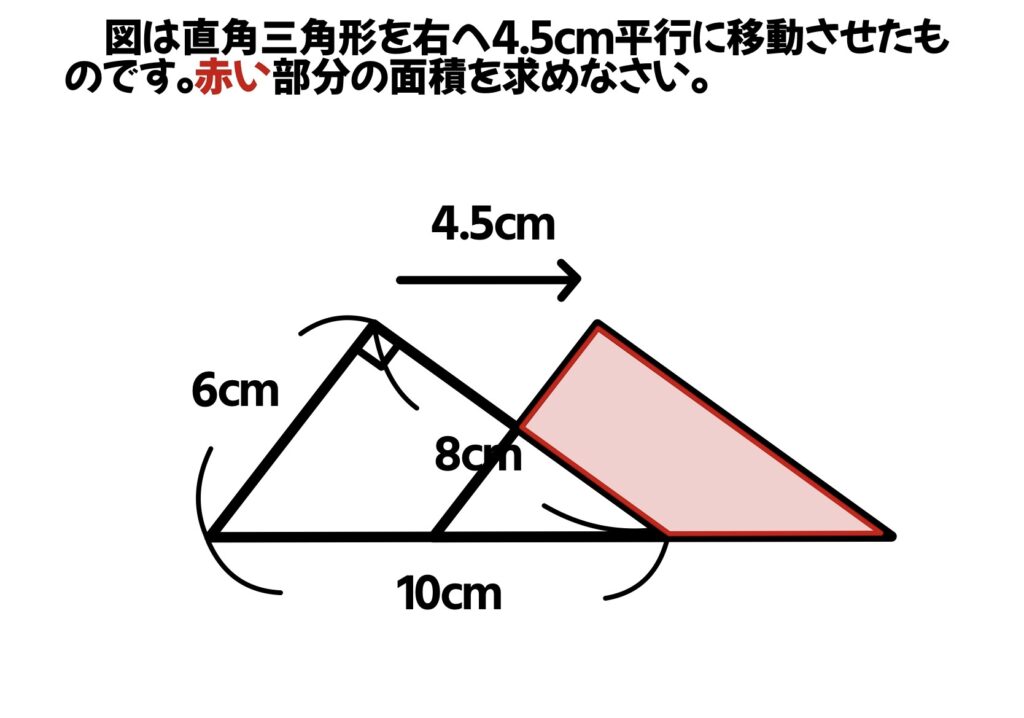
問題⑫
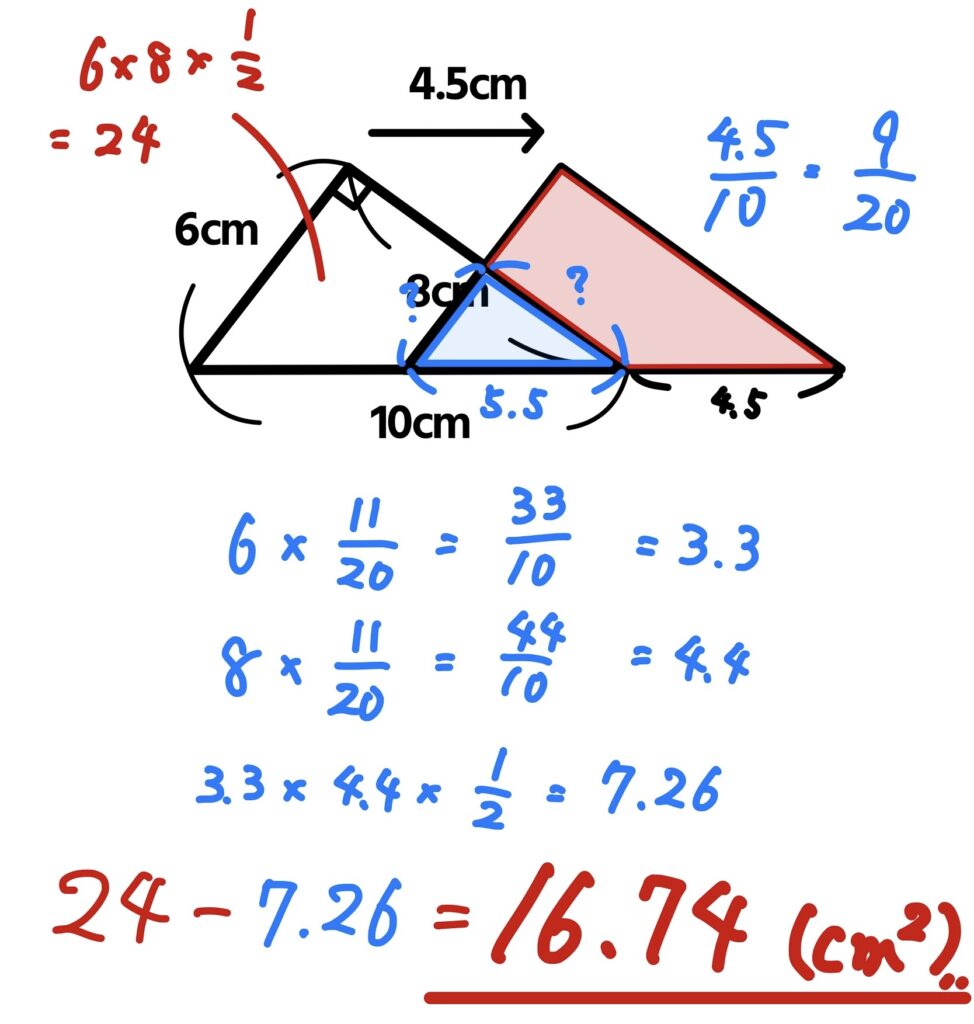
図は直角三角形を右へ4.5㎝平行に移動させたものです。赤い部分の面積を求めなさい。
角度を求める問題20選!小学生から中学生向けの図形クイズを紹介!
面積を求める問題35選!子供から大人まで楽しめる図形のクイズを紹介!
算数の面白い問題45選!小学生から大人まで楽しめるクイズ
まとめ
大人が算数を学び直すメリットは多岐にわたります。日常生活での論理的思考力の強化や脳の活性化に至るまで、学び直しは大人になった私たちの生活に確かなプラスの影響をもたらします。
また、自己研鑽や新たな挑戦へのきっかけとなりますので、積極的に取り組んでみることをおすすめします。

↑↑↑子供の学習や大人の脳トレに最適!!
投稿者プロフィール

-
現役で数学を教えている中学校の先生です。中学の数学のプリントやICT関連の情報、ブログでは道徳や学級レクのネタも発信しています。
このサイトはアフィリエイト広告(Amazonアソシエイト含む)を掲載しています。
最新の投稿
 ブログ2026年1月30日【国民の祝日クイズ45問】意外と知らない日付とルールを4択問題でチェック!
ブログ2026年1月30日【国民の祝日クイズ45問】意外と知らない日付とルールを4択問題でチェック! ブログ2026年1月25日小・中学生の塾はいつから?教員が考える本当に意味のあるタイミング
ブログ2026年1月25日小・中学生の塾はいつから?教員が考える本当に意味のあるタイミング ブログ2026年1月24日教員が本音で答える|保護者からよく聞かれる勉強の悩み8選
ブログ2026年1月24日教員が本音で答える|保護者からよく聞かれる勉強の悩み8選 お知らせ2026年1月18日ネット副業は本当にバレない?教員が知っておくべき現実と境界線
お知らせ2026年1月18日ネット副業は本当にバレない?教員が知っておくべき現実と境界線