
円の面積を求める時も、円周の長さを求める時も、あり前のように登場する円周率3.14…。「そもそも円周率って何?」「なんで3.14なの?」と思った事はないでしょうか?
今回は、円周率が3.14である理由、どのようにして3.14が発見されたのかについて、詳しく解説していきたいと思います!

この記事を読めば、円周率3.14の正体について理解できますよ!
RISU算数(タブレット学習教材)を現役数学教師がレビューしました!

↑↑↑子供に出題すると盛り上がりますよ!!
そもそも円周率って何?

円周率は小学生の時は3.14で習い、中学生になるとπ(パイ)を使いますよね。円周率は円の外周の長さ(円周)と、その円の直径の長さの比率を表す数字です。直径が1㎝の円だとすると、その円周の長さは約3.14㎝となります。
円周:直径 × 円周率(3.14)
つまり、どんな大きさの円でも、円周を直径で割ると3.14になります。直径が2㎝であれば円周は6.28…㎝、直径が3㎝であれば円周は9.42…㎝となっていきます。この特別な数字が円周率と呼ばれ、実際には小数点が続く無限の数字です。
誰が発見したの?
円周率を発見したのは、古代ギリシャの数学者であるアルキメデスが発見したと言われています。
アルキメデスは紀元前287年~212年頃の最も天才的な数理科学者で、シチリア島で生まれたとされています。今では分数や小数などを量としてあたり前のように数として認識して、自由に四則演算ができるようになったのも、アルキメデスのような大天才が多くの知見を残してくれたおかげなのです。
以下ではアルキメデスがどのように3.14を発見したのか紹介していきます。
3.14を求めてみる
アルキメデスが約4000年前に円周率3.14求めたやり方を紹介します。
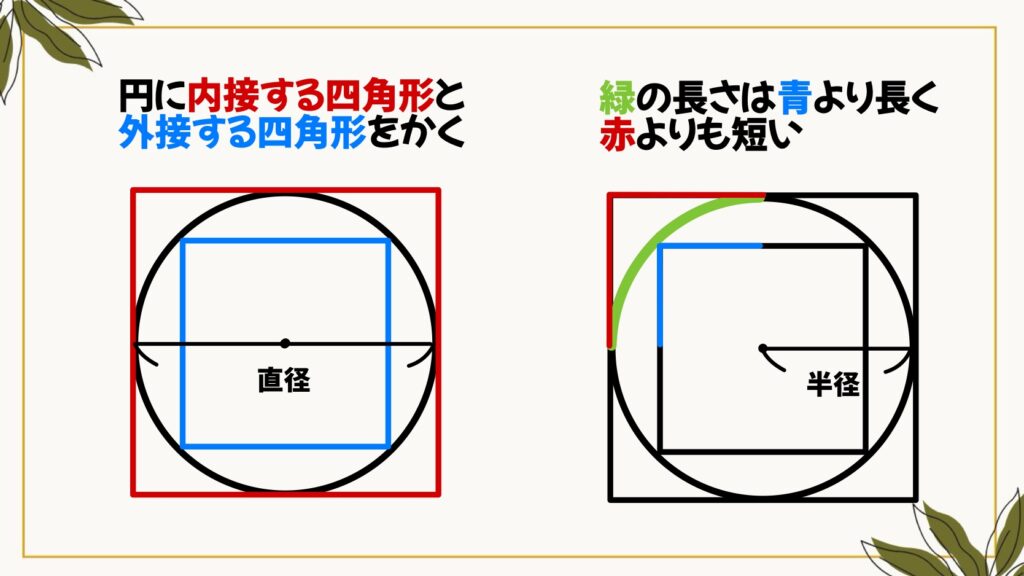
まず、円の内側にぴったりはまる(内接する)青い正方形と、外側に円の直径がぴったりとはまる(外接する)赤い正方形をかきます。
画像の右側のように、緑の部分は青の部分より長く、赤い部分よりも短くなります。(青<緑<赤)
つまり、円周の長さは内側の正方形の周の長さよりも長く、外側の正方形の周の長さよりも短くなることが分かります。
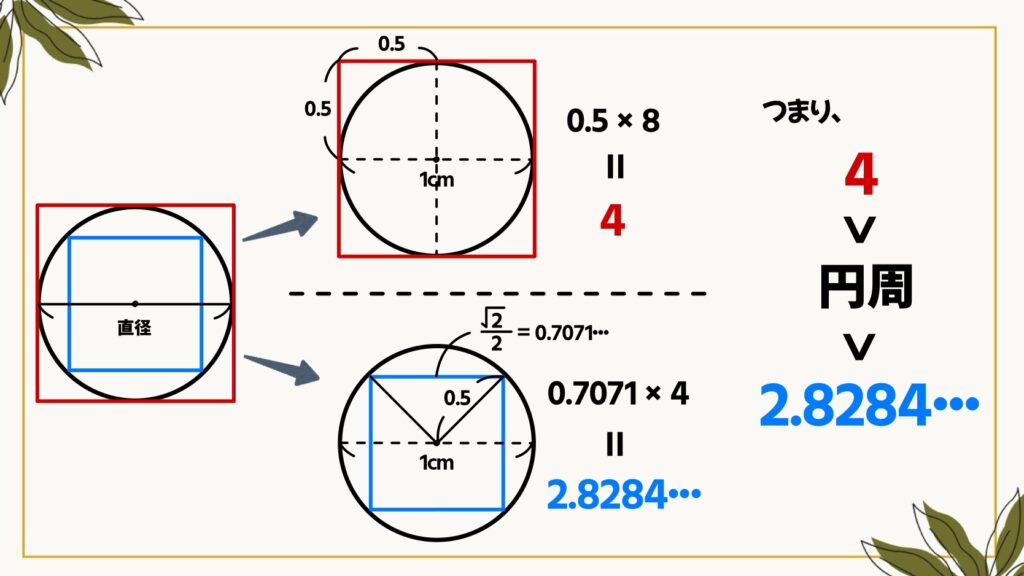
円の直径を1㎝とすると、外側の正方形の周の長さは8㎝となります。内側の正方形は、三平方の定理を使うと1辺が√2/2㎝となるので、周の長さは√2/2×4=2.8284…㎝となります。
よって、円周の長さは2.8284…㎝より大きく、4㎝よりも小さいことが分かります。
2.8284…<円周<4
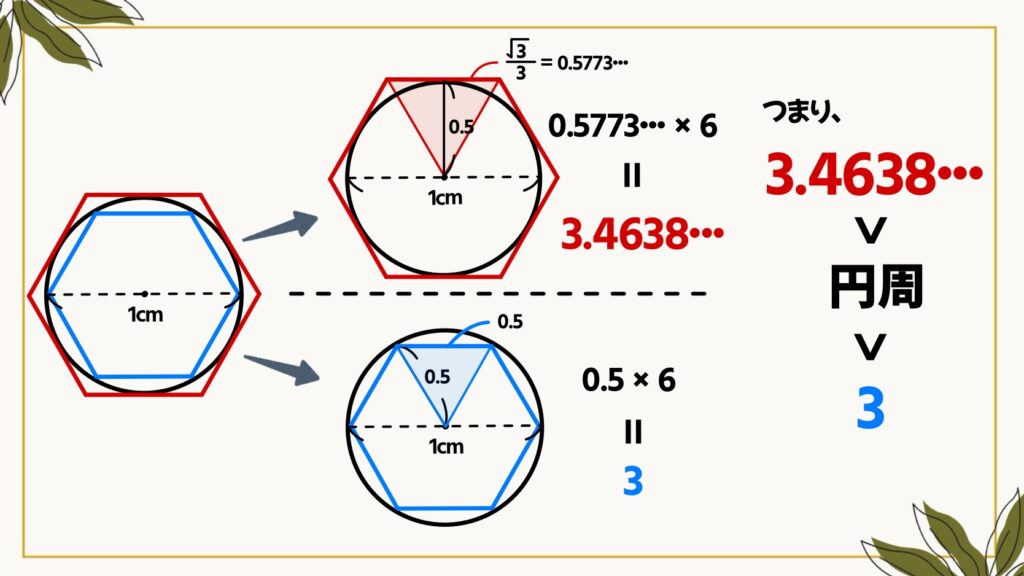
同じように円の中に今度は正六角形をかいてみます。円周の長さは内側の正六角形の周の長さよりも長く、外側の正六角形の周の長さよりも短くなります。
外側の正六角形は、三平方の定理を使うと1辺が√3/3㎝となり、周の長さは√3/3×6=3.4638…となり、内側の正六角形の周の長さは3㎝となります。
よって、円周の長さは3㎝よりも大きく、3.4638…㎝よりも小さいことが分かります。
3<円周<3.4638
もう分かりましたよね?この円にそれぞれ内接、外接する正多角形の角を増やしていくと、円周率は3.14…㎝に近づいていくというわけです。
ちなみに、正16角形まで調べると、3.14084…<円周<3,14286…が分かります。かなり皆さんの知っている円周率に近づいていますよね!

現在では円周率は100兆ケタまで計算されたらしいよ!
円周率を確かめてみよう
子供に3.14を教えようと思ったら、上のようなやり方では少し難しいので、もっと簡単に3.14を求めてみましょう。
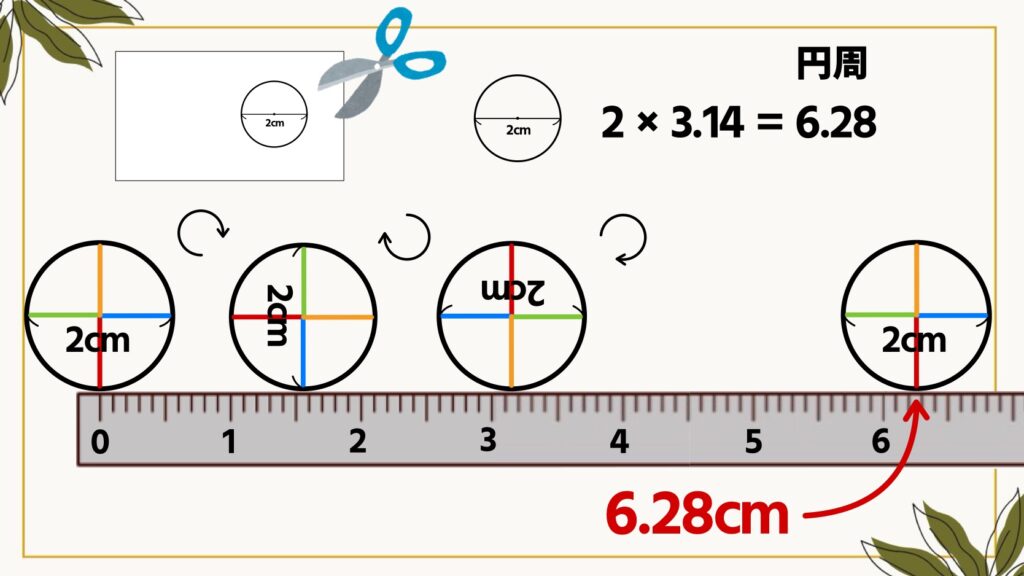
紙にコンパスで円をかきましょう。直径が1㎝、2㎝、3cmの円を3種類ほどかき、ハサミで切り抜いていきます。
切り抜いた円に印をつけて、定規の上で1回転させてみましょう。1㎝の円であれば3.14㎝、2㎝の円であれば6.28㎝、3㎝の円であれば9.42㎝・・・。どれも必ず直径の3.14倍となりますよね。
このやり方であれば、子供でも3.14という数字を少し身近に感じることができるかもしれません。
まとめ
いかがだったでしょうか?覚えるだけではなんだか味気ない円周率でも、理由が分かるとすこしワクワクするような感覚になりませんか?
円周はどんなに大きな円でも必ず直径×3.14になっている。このように円周率について理解することは、算数が好きになるきっかけになるかもしれませんね。

↑↑↑子供に出題すると盛り上がりますよ!!
投稿者プロフィール

-
現役で数学を教えている中学校の先生です。中学の数学のプリントやICT関連の情報、ブログでは道徳や学級レクのネタも発信しています。
このサイトはアフィリエイト広告(Amazonアソシエイト含む)を掲載しています。
最新の投稿
 ブログ2026年2月2日Keynoteの便利機能8選|知らないと損する使い方まとめ
ブログ2026年2月2日Keynoteの便利機能8選|知らないと損する使い方まとめ ブログ2026年1月30日【国民の祝日クイズ45問】意外と知らない日付とルールを4択問題でチェック!
ブログ2026年1月30日【国民の祝日クイズ45問】意外と知らない日付とルールを4択問題でチェック! ブログ2026年1月25日小・中学生の塾はいつから?教員が考える本当に意味のあるタイミング
ブログ2026年1月25日小・中学生の塾はいつから?教員が考える本当に意味のあるタイミング ブログ2026年1月24日教員が本音で答える|保護者からよく聞かれる勉強の悩み8選
ブログ2026年1月24日教員が本音で答える|保護者からよく聞かれる勉強の悩み8選





