錐の体積はなぜ１/３になるのかを解説！小中学生向けイラスト付きで分かりやすい

　円錐や四角錐などのいわゆる「錐体」の体積を求めるとき、同じ底面積で同じ高さの円柱や四角柱の体積の１/３になるのはなぜでしょうか？

　この記事では、小中学生向けに水を使ったシンプルな実験をイラストを使って分かりやすく解説をしていきたいと思います。また、分かりやすい証明を用いた方法でも１/３を解説していきたいと思います。

　また、本来実際の模型を使い、その模型に水を入れて説明することが一番良いんですが、立体の模型は思いのほか高価な物なので、模型などを用意できないけど子供に分かりやすく説明したい場合はこちらのサイトの画像をお使いください！

デキタスを現役中学校教師がレビュー！の記事はこちら

RISU算数（タブレット学習教材）を現役数学教師がレビューしました！

　水を使った解説

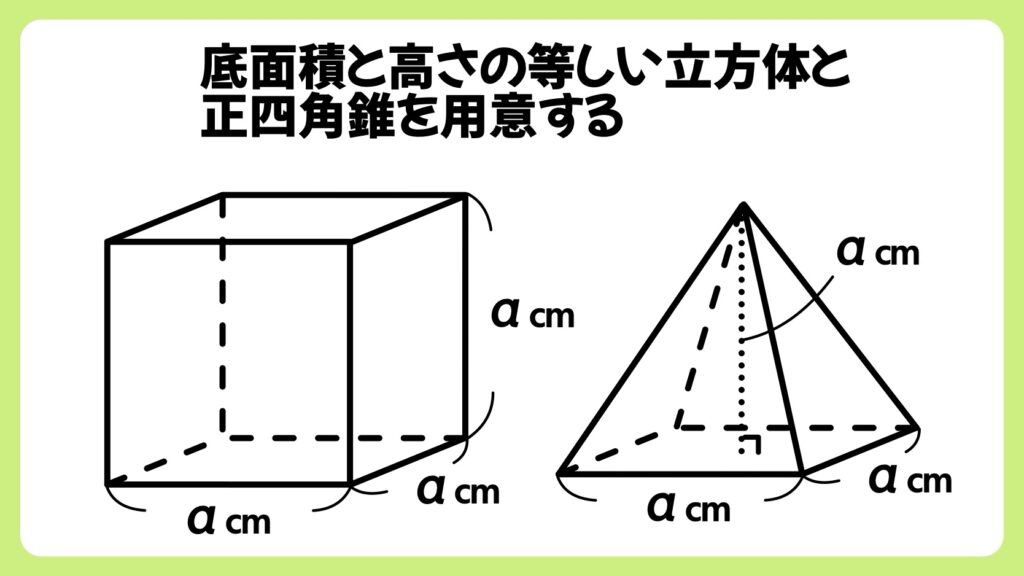
　まずは上の画像のような、同じ底面積、同じ高さの立方体と正四角錐を用意します。

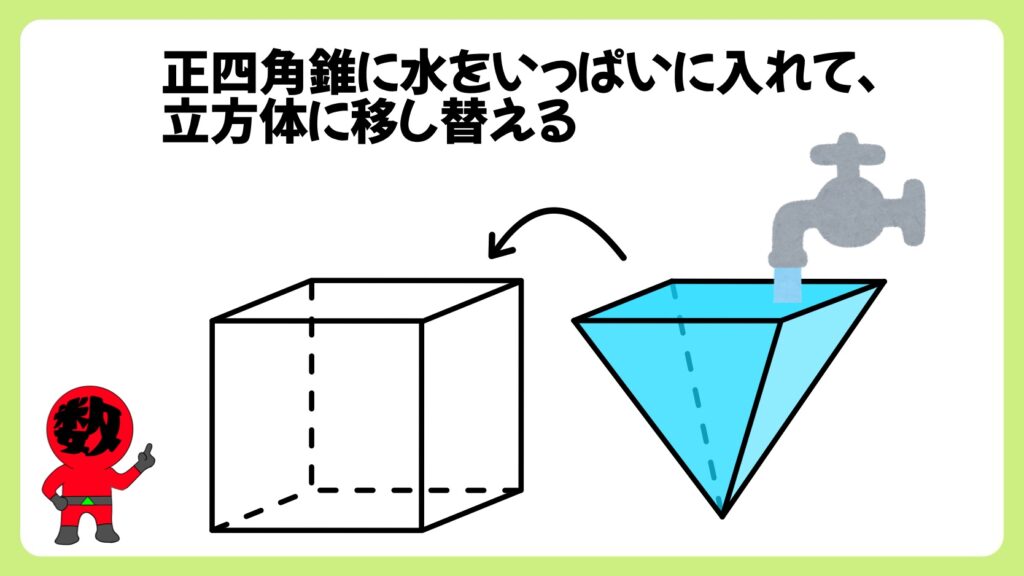
　この正四角錐に水を一杯に入れ、正四角錐に水を移し替えていきます。

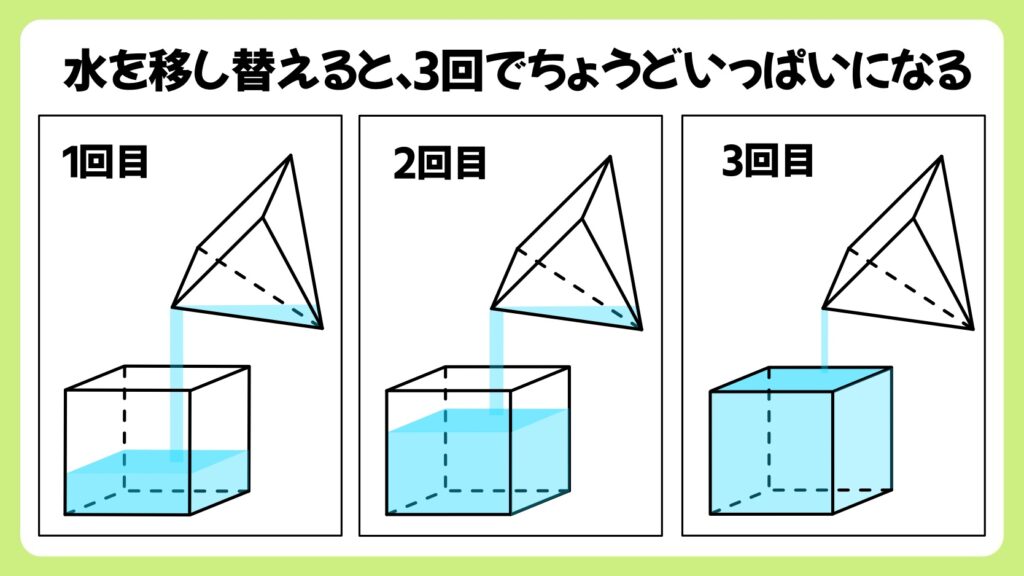
　実際に模型を使って、子供の前でやってみたことがあるのですが、「何杯でいっぱいになると思う？」と質問すると、多くの子供が「２杯！」と答えます。確かに見た目の大きさからすると２杯くらい見えるんですよね。

　実際には３杯で正四角錐はちょうどいっぱいになります。

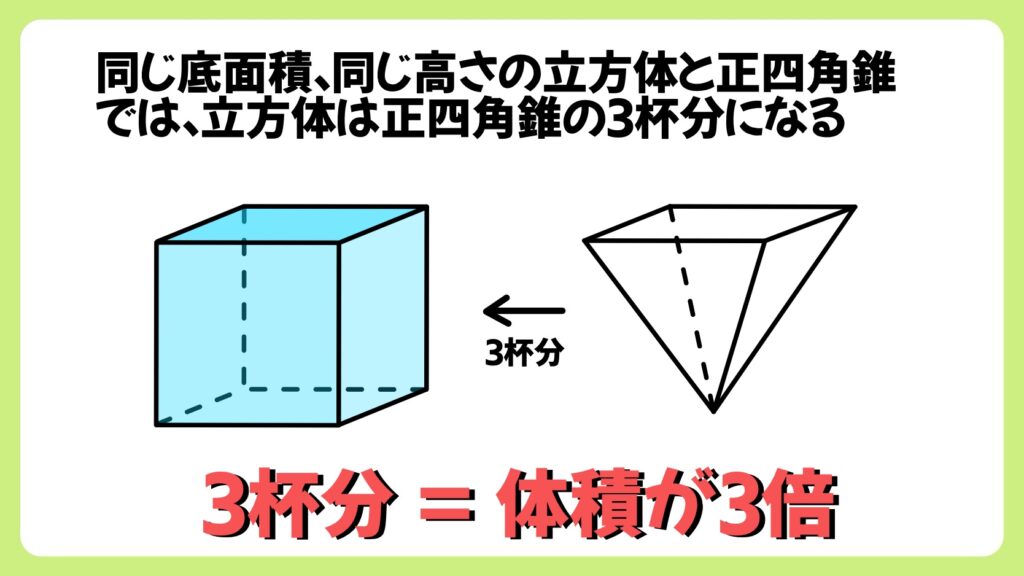
　つまり、同じ底面積、同じ高さの立方体と正四角錐では、立方体は正四角錐の３杯分になるということが分かるので、体積が３倍であることが分かります。

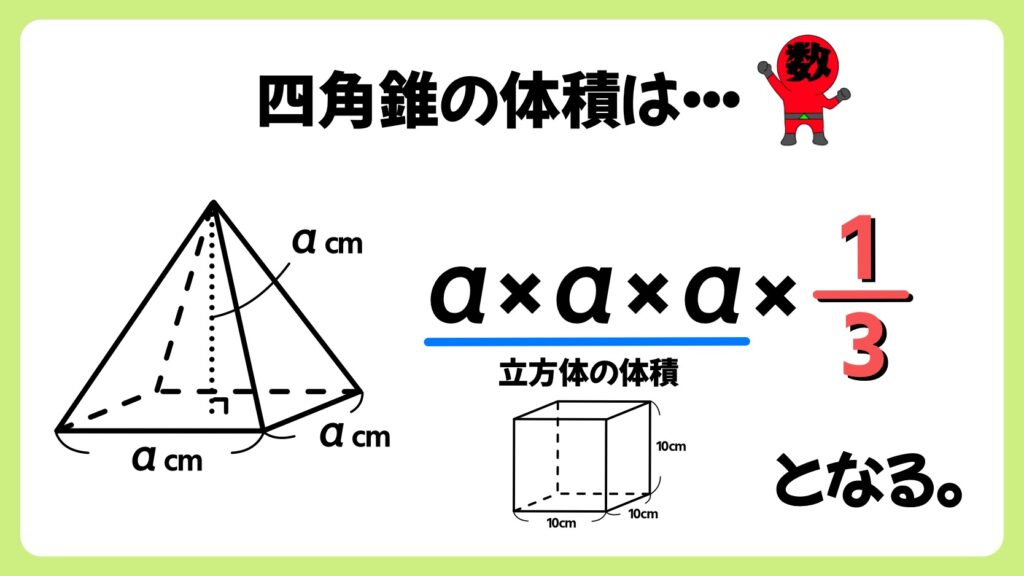
　つまり、この正四角錐の体積は、同じ底面積、同じ高さを持つ立方体の体積の１/３となります。

　V＝１/３Sa であることの証明

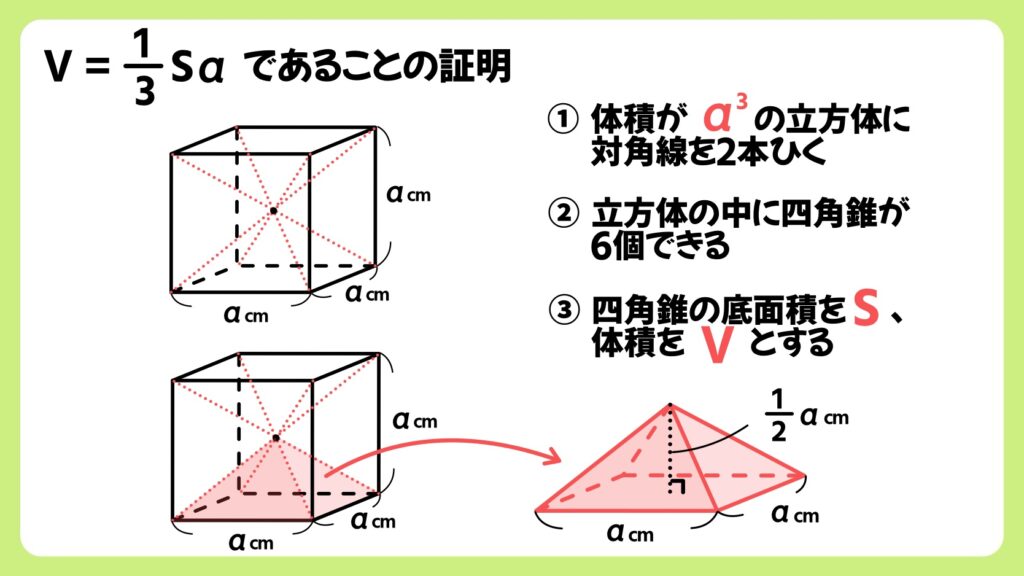
　１辺がacmの立方体に対角線を２本ひくと、立方体の内部に正四角錐が６個作ることができます。この正四角錐は、底面の正方形の１辺がacmで、高さが１/２acmの正四角錐となります。

　この正四角錐の底面積をS、体積をVとすると、

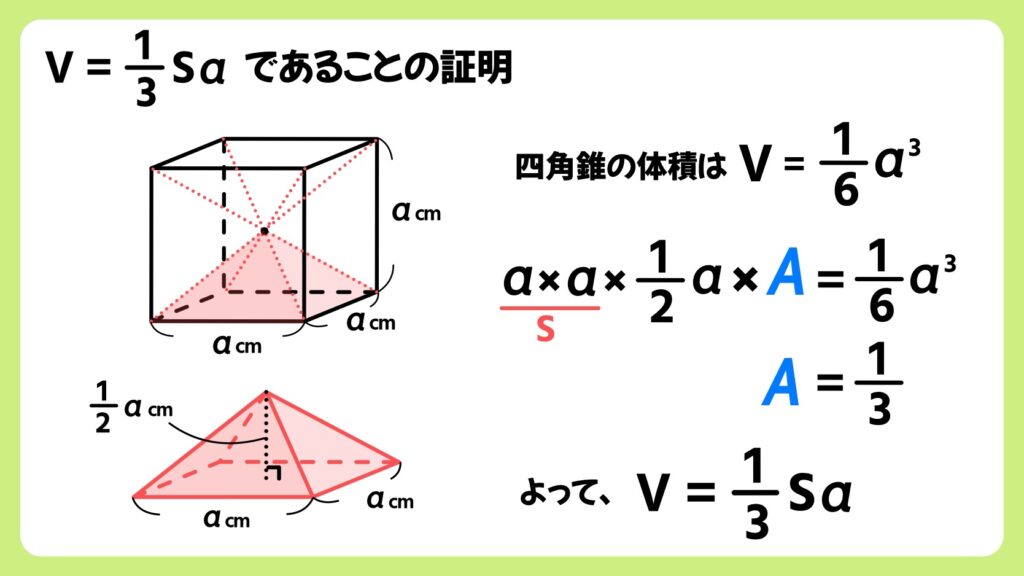
正四角錐の体積は１/６a^3となり、V＝１/３Saであることが分かります。

　まとめ

　錐体の体積の求め方に出てくる１/３の意味がご理解いただけでしょうか？実際に見せて説明することが一番理解しやすいですが、模型などを準備できない場合はぜひこの記事の画像をご活用ください。

　円錐や三角錐など、他の錐体についても同様の説明ができます。数学の魅力はこのようなシンプルな実験でも感じることができますね！

多角形の内角の和の求め方はなぜ180°－(n－2)なのか？イラストで分かりやすく！