【おうぎ形の公式】面積・弧の長さ・中心角の求め方をイラストで分かりやすく解説！

小中学生がとても苦手意識の強いおうぎ形、特に中学数学で登場するおうぎ形の公式は子供がとても混乱しやすい内容です。

この記事では、１５年間数学の教員をしている私が、扇形（おうぎ形）の面積、中心角、弧の長さをできるだけわかりやすく解説したいと思います。

この記事を通して、ぜひ扇形についてマスターしてくださいね。

小学生はπ（パイ）を3.14にして考えてみてね！

RISU算数のレビューと感想！現役数学教師が使ってみました！

1. 扇形とは
2. 面積の求め方
3. 半径と弧の長さから面積を求める
4. 弧の長さの求め方
5. 弧の長さから中心角を求める
6. 面積から中心角を求める
7. まとめ

学校の先生がクラスの子供に出題しておもしろい問題を作りました！！

扇形とは

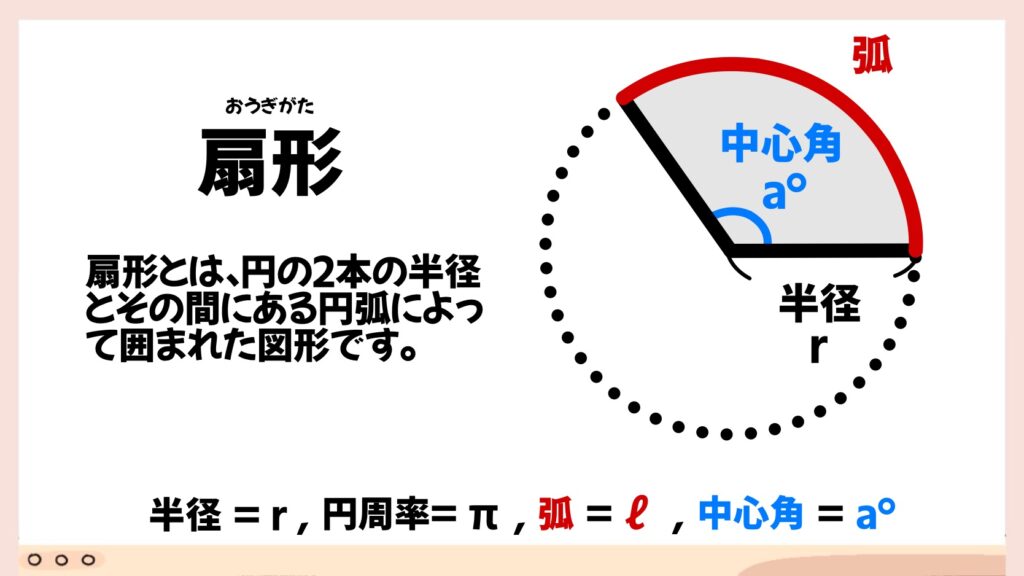
まずは扇形（おうぎがた）について、基本的なことを確認しておきましょう。

扇形とは、円の２本の半径と、その間にある円弧（半径同士を繋いでいる曲線部分）によって囲まれた図形のことをいいます。ピザの欠片のように、円の一部を切り取った図形と考えましょう。

S は扇形の面積、π は円周率、r は円の半径、a は中心角、ℓは弧の長さを表します。

デキタスを現役中学校教師がレビュー！タブレット学習教材って実際どうなの？

面積の求め方

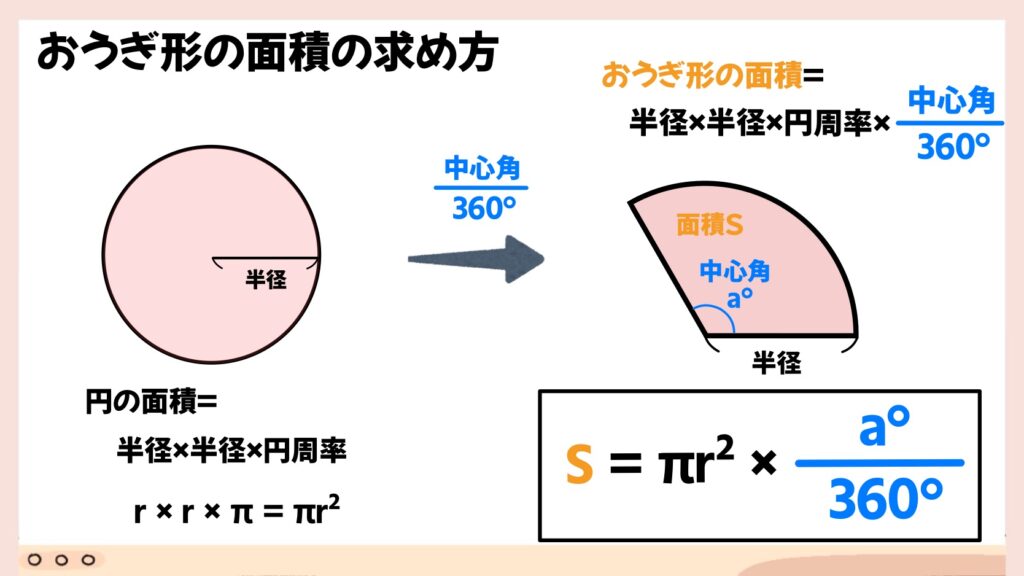
扇形の面積を求めるときは、もとの円と比べてどれくらいの大きさなのか、を考えます。扇形と同じ半径をもつ円の面積に、中心角の割合をかければ求められます。

扇形の中心角の1° というのは、円の中心角 360° の360分の1の大きさです。例えば、中心角 40° の扇形の面積は、半径が等しい円の面積の360分の40、つまり、9分の1の大きさになります。

新品のピザの面積を求めてから「360分の中心角」をかけることで求められるんだね！

半径と弧の長さから面積を求める

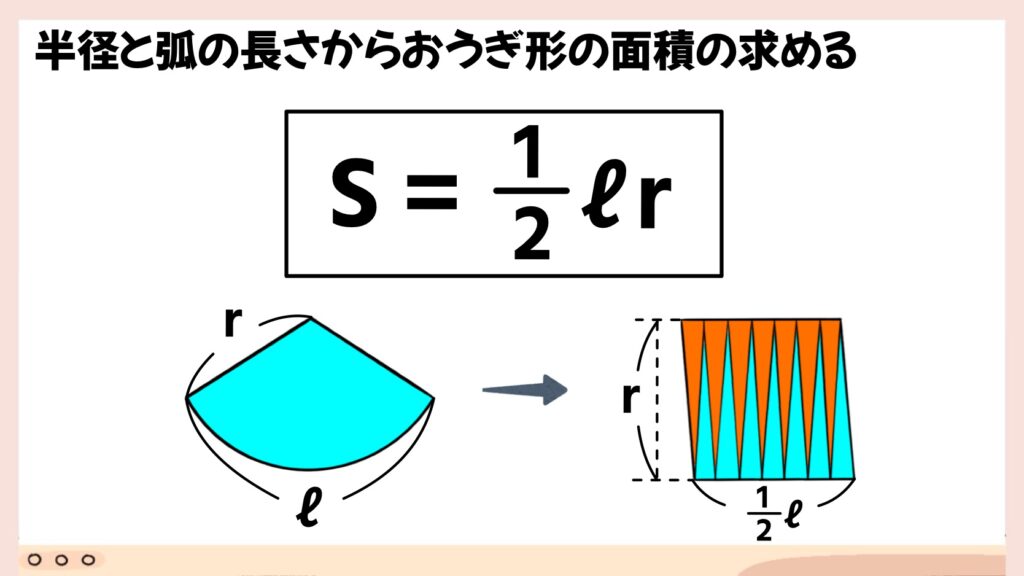
扇形にはもう一つ、面積の求め方があります。

図のように、扇形を限りなく細かく切っていき、それを互い違いに並べると平行四辺形が出来上がります。縦の長さは半径ｒとなり、横の長さは弧の長さの半分になるので、１/２ℓとなります。

よって、面積S＝１/２ℓｒという式が成り立ちます。　

扇形の面積公式を覚えたら、ついでに弧の長さ公式も一緒に覚えてしまいましょう。覚えておくと大変便利です！

弧の長さの求め方

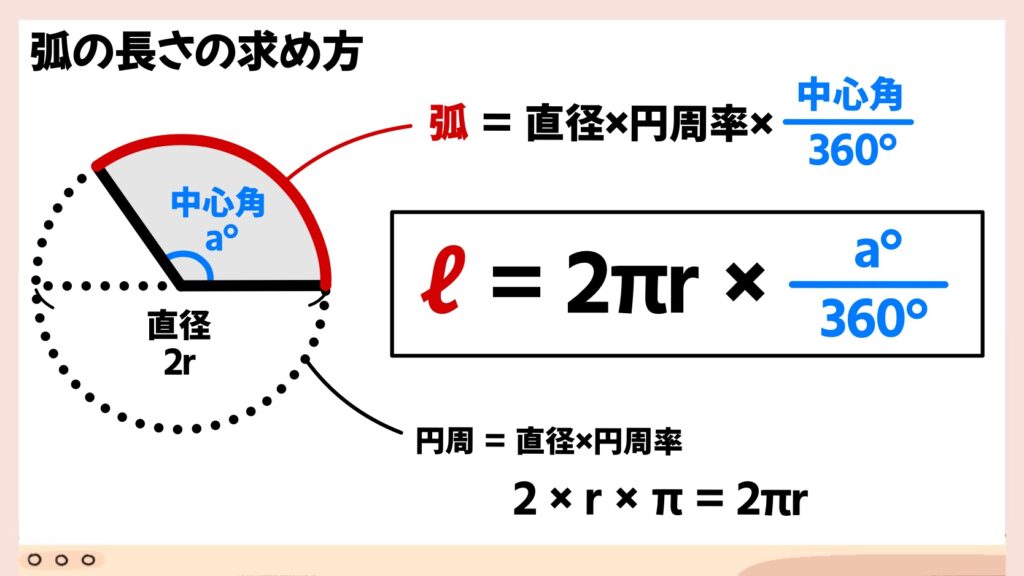
扇形の弧の長さは、面積を求めるときと同じ考え方で求めることができます。もとの円の円周と比べてどれくらいの長さなのか、を考えましょう。扇形と同じ半径をもつ円の円周の長さに、中心角の割合をかければ求められます。

例えば、中心角 120° の扇形の弧の長さは、半径が等しい円の面積の360分の120、つまり、3分の1の大きさになります。

考え方は面積の求め方と一緒だよ！

弧の長さから中心角を求める

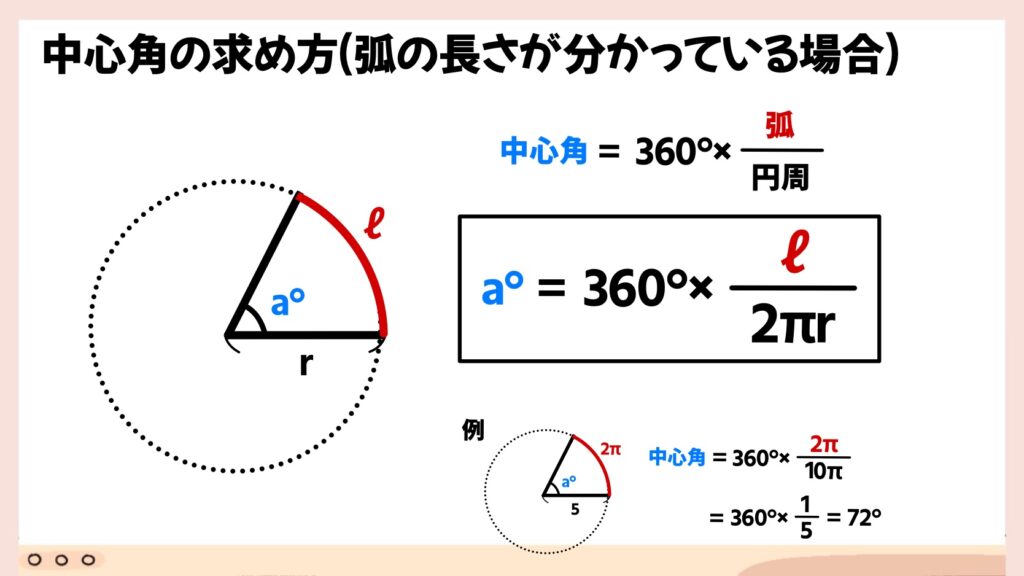
弧の長さから中心角を求める方法を紹介します。

弧の長さが分かっている場合、円周の長さと弧の長さの割合を求めます。例えば、弧の長さが２π㎝、円周の長さが10π㎝だった場合、その割合は5分の1となる。つまり、中心角も360°の5分の1だということが分かるので、72°であることが分かります。

面積から中心角を求める

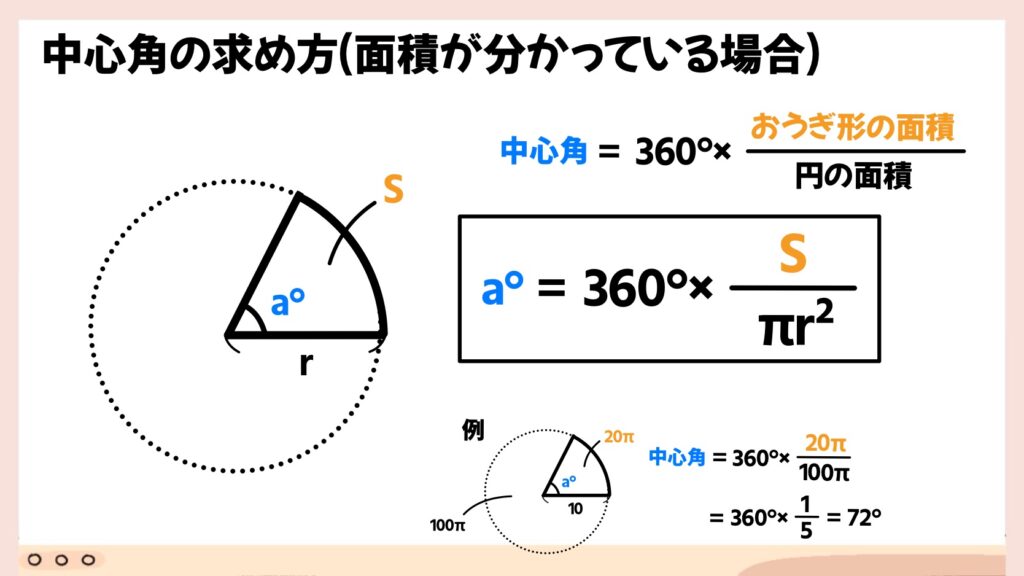
次に面積が分かっている場合の中心角の求め方を紹介します。考え方は弧の長さが分かっている時と変わりません。

扇形の面積が円全体の面積の割合を占めているかを求めます。

例えば、扇形の面積が20π、円全体の面積が100πのとき、割合は5分の1となるので、中心角も360°の5分の1であることが分かります。

１つ理解できれば、すべてが繋がるよね！

まとめ

扇形の面積や弧の長さの公式は暗記するようなものではありません。面積も弧の長さも中心角も、元の円に対してどれくらいの割合かを意識すれば決して難しいものではありません。

ぜひこの機会に、扇形についてマスターしてください！

投稿者プロフィール

hiro先生: 教育×ICTクリエイター｜教育メディア運営
 Apple Teacher、Kahoot!認定クリエイター。
授業で使える算数・数学問題、思考力を育てるクイズ、ICT活用法を発信。 運営する教育ブログは月間15万PV。
教員として5種類の兼業を経験し、ストック型副業で月10万円の収益を構築。
 電子書籍はAmazonベストセラーを獲得し、書籍出版も経験。
現在は教育コンテンツ制作、デジタル教材開発、教員の働き方や副業について発信中。 SNS総フォロワー数は約3万人。