分数の割り算はなぜひっくり返す？逆数をかける理由を解説！

分数は、子供にとって躓きやすい算数の分野です。その理由として考えられるのは、分数を頭の中でイメージしにくいことです。

特に分数の割り算では、かけ算に直して分母と分子をひっくり返す（逆数にする）という作業があります。単純に「かけ算に直してひっくり返す」と覚えれば問題は解けるのですが、ただ覚えただけでは算数の力は身につかないでしょう。

この記事では、分数の割り算はかけ算にして分母と分子をひっくり返すのか、１５年間数学を教えている僕が子供にも分かりやすく解説をしていきたいと思います！

２種類の方法で解説しますね！

↑↑↑学校の先生におすすめ！！

図で理解しよう

まずは６÷２で考えましょう。誰もが答えは３であることは分かります。おそらく多くの人が２×〇＝６で、〇に入る数字は３だから、答えは３！と考えたのではないでしょうか？

次に、６÷２＝３を水を使って具体的に考えてみましょう。

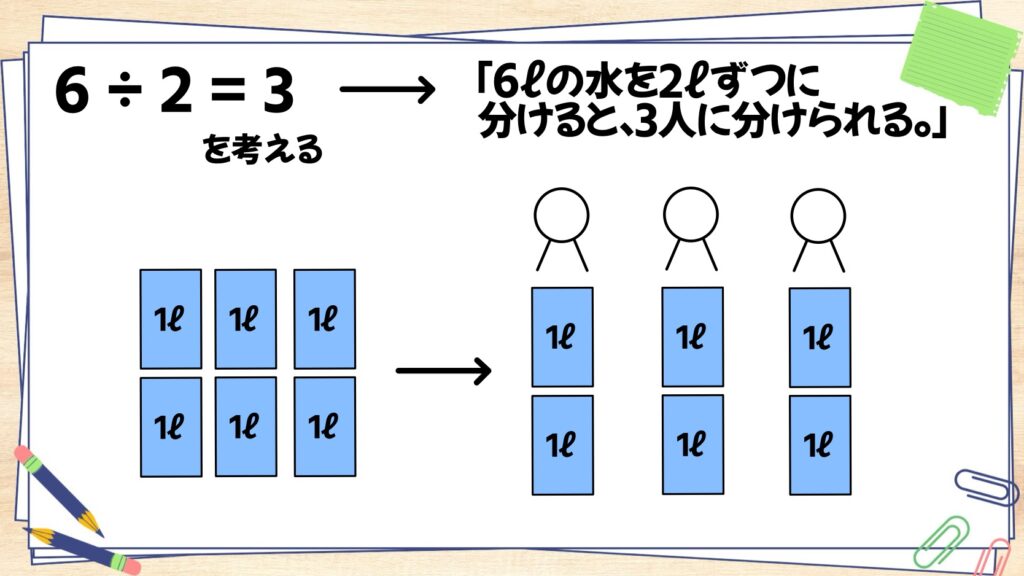
６÷２＝３を「６ℓの水を２ℓずつに分けると、３人に分けられる。」と考えると、下の図のようになりますよね。

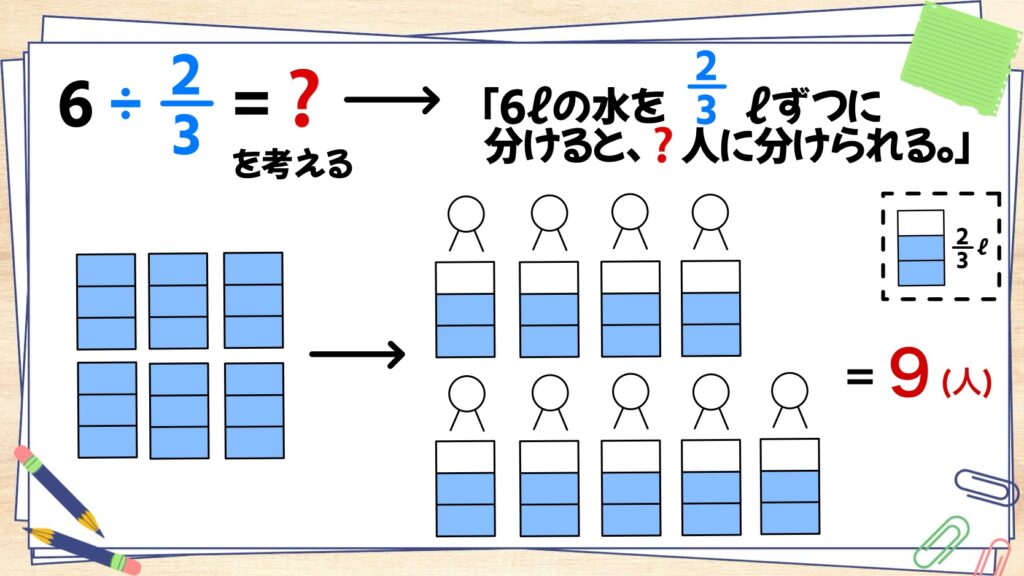
６÷２/３＝？を考えましょう。上と同じように具体的に考えうと「６ℓの水を２/３ℓずつ分けると、？人分けられる。」と考えます。実際に分けてみると、下の図のように、９人に分けることができることが分かります。

つまり、

６÷２/３＝９

であることが分かりますね。

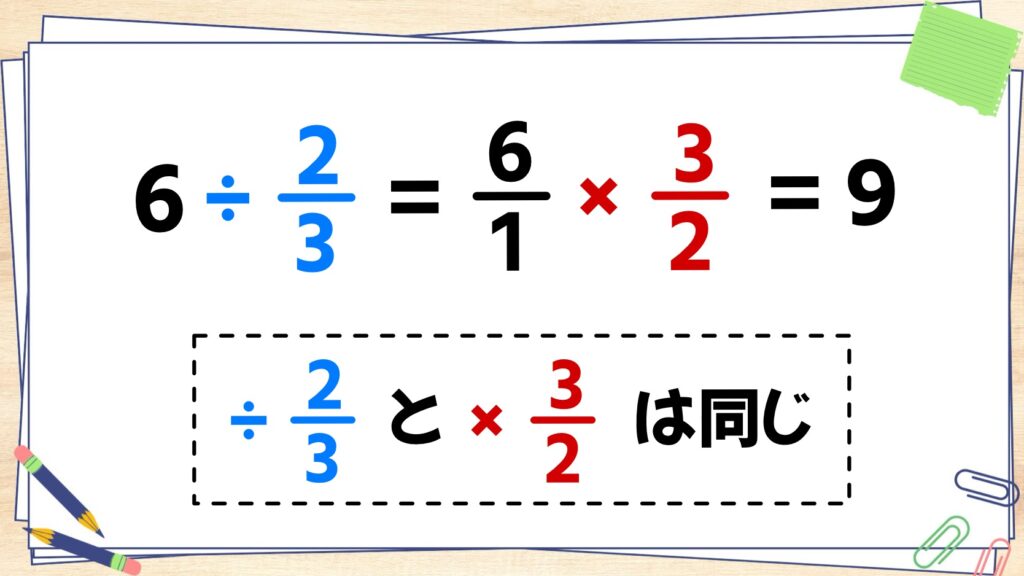
６に何をしたら９になるかを考えると、６×３/２＝９となることが分かるので、

÷２/３と×３/２は同じ

ということが言えますね。

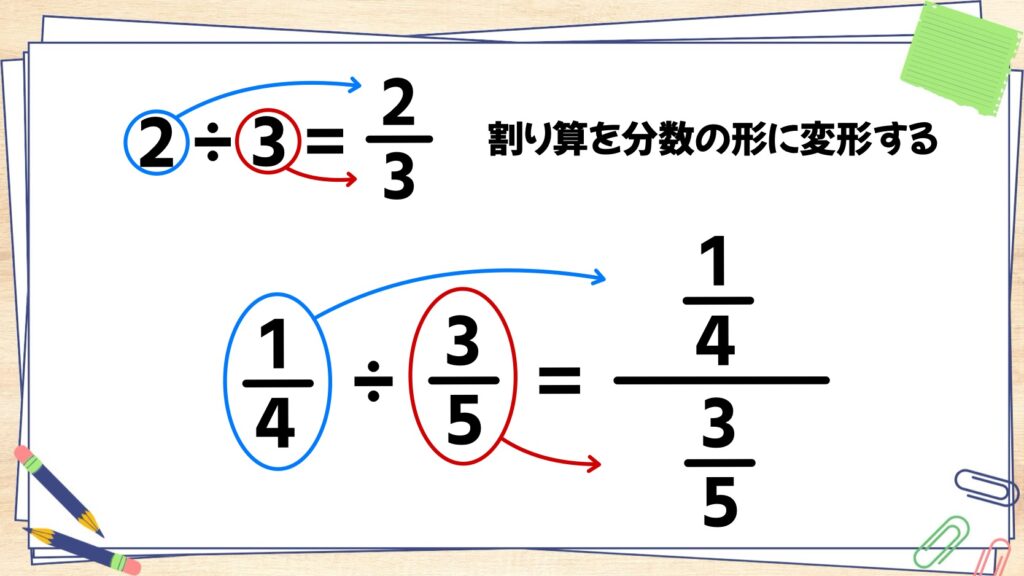
２÷３＝２/３のように、割り算は分数に変形することができます。これを分数の割り算で考えてみましょう。

１/４÷３/５を分数の形に直してみると、下の図のように変形することができます。この「分数の分数」の形を「繁分数」といいます。

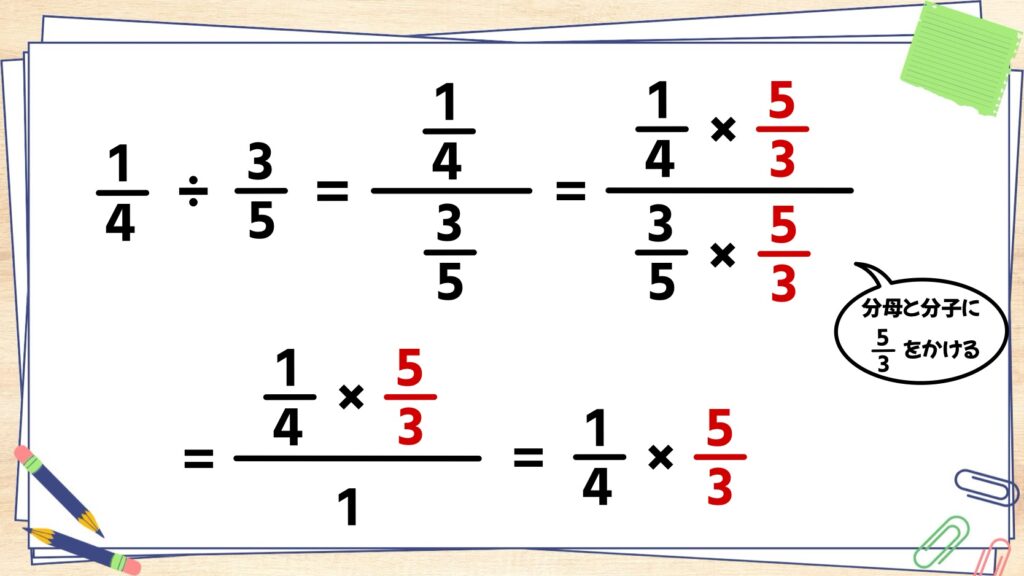
分数は、分母と分子に同じ数をかけても数が変わらないという性質があります。この性質を使って、１/４分の３/５の分母と分子にそれぞれ５/３をかけます。

計算すると、分母が１になり、分子が１/４×５/３となります。

結果的に、１/４÷３/５=１/４×５/３

分数の割り算が逆数のかけ算になる理由を理解すると、分数に対する理解が深まります。「分母同士、分子同士かけるんだよ」とか、「分母と分子をひっくり返すんだよ」とただ覚えて問題が解けるようになっても、算数の本質的な力は身につきません。

分数だけではないですが、頭の中でイメージができるようになると、算数への理解を一層深めることができますよ！

↑↑↑学校の先生におすすめ！！

hiro先生: 教育×ICTクリエイター｜教育メディア運営
 Apple Teacher、Kahoot!認定クリエイター。
授業で使える算数・数学問題、思考力を育てるクイズ、ICT活用法を発信。 運営する教育ブログは月間15万PV。
教員として5種類の兼業を経験し、ストック型副業で月10万円の収益を構築。
 電子書籍はAmazonベストセラーを獲得し、書籍出版も経験。
現在は教育コンテンツ制作、デジタル教材開発、教員の働き方や副業について発信中。 SNS総フォロワー数は約3万人。