分数の割り算はなぜひっくり返す？逆数をかける理由を解説！

分数は、子供にとって躓きやすい算数の分野です。その理由として考えられるのは、分数を頭の中でイメージしにくいことです。

特に分数の割り算では、かけ算に直して分母と分子をひっくり返す（逆数にする）という作業があります。

単純に「かけ算に直してひっくり返す」と覚えれば問題は解けるのですが、ただ覚えただけでは算数の力は身につかないでしょう。

この記事では、分数の割り算はかけ算にして分母と分子をひっくり返すのか、１５年間数学を教えている僕が子供にも分かりやすく解説をしていきたいと思います！

２種類の方法で解説しますね！

ブログ

【RISU算数のレビューと口コミ】現役数学教師がタブレット学習教材を使ってみた！

2023年12月3日

ブログ

なぜ円周率は３．１４なのか？求め方を分かりやすく紹介！

2024年6月17日

ブログ

2024年6月2日

1. 分数の割り算で子どもがつまずく理由
2. 図で理解しよう
3. 「割り算→分数」の変型で考える
4. 分数の割り算は中学校でも使う
5. まとめ

↓[授業準備を０にする】小６算数授業テンプレートをnoteで販売しています。　

分数の割り算で子どもがつまずく理由

分数の割り算は、小学校の算数の中でも特につまずく子どもが多い単元です。

その理由の一つは、量のイメージがしにくいことです。整数の「6÷2」ならイメージしやすいですが、「6÷2/3」となると、何を求めているのか分からなくなってしまう子どもも少なくありません。

また、学校では「ひっくり返してかける」と計算方法を学びますが、計算のやり方だけを覚えてしまう子どもも多いです。

もちろん答えは出せるようになりますが、「なぜそうなるのか」を理解していないため、肝心の納得感を得られないまま暗記のような学習になってしまいます。

そして、分数の割り算で欠かせないのが逆数の理解です。逆数をただ「ひっくり返した数」と覚えているだけでは、本当の意味で分数を理解したことにはなりません。

だからこそ、分数の割り算は計算方法を覚えるだけでなく、「なぜ逆数をかけるのか」を図や具体物を使って理解することが大切なのです。

図で理解しよう

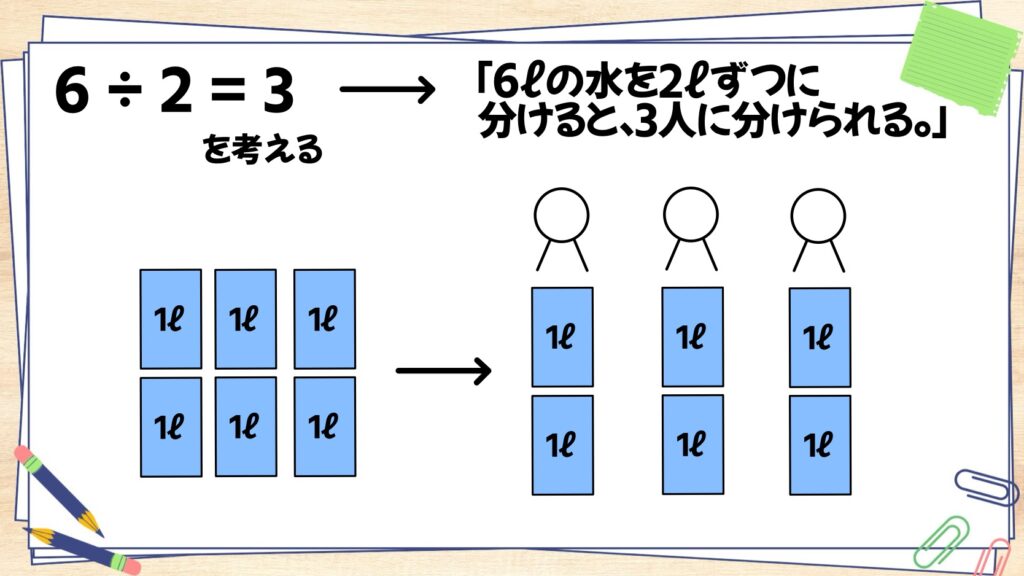
まずは６÷２で考えましょう。誰もが答えは３であることは分かります。おそらく多くの人が２×〇＝６で、〇に入る数字は３だから、答えは３！と考えたのではないでしょうか？

次に、６÷２＝３を水を使って具体的に考えてみましょう。

６÷２＝３を「６ℓの水を２ℓずつに分けると、３人に分けられる。」と考えると、下の図のようになりますよね。

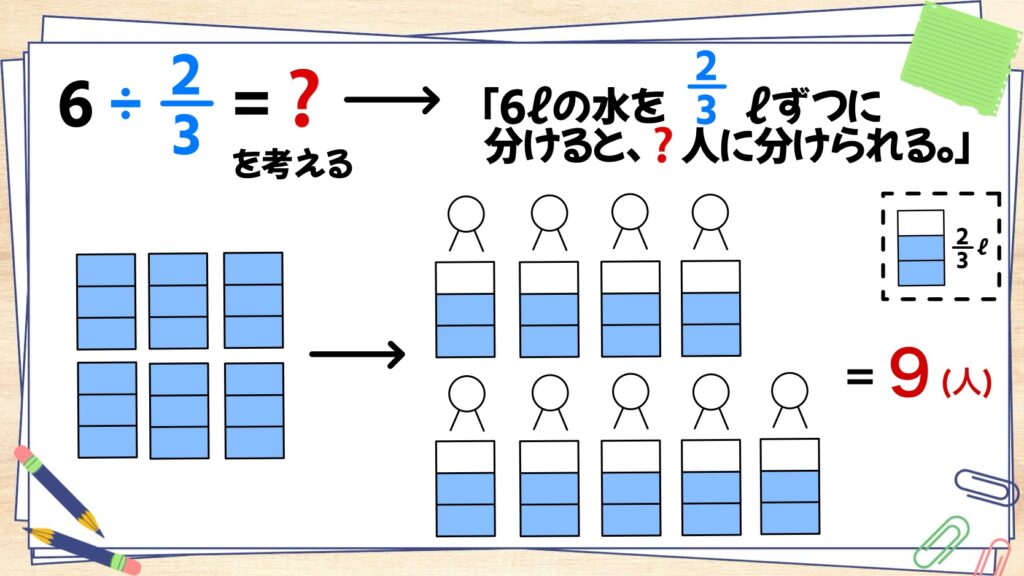
６÷２/３＝？を考えましょう。上と同じように具体的に考えうと「６ℓの水を２/３ℓずつ分けると、？人分けられる。」と考えます。実際に分けてみると、下の図のように、９人に分けることができることが分かります。

つまり、

６÷２/３＝９

であることが分かりますね。

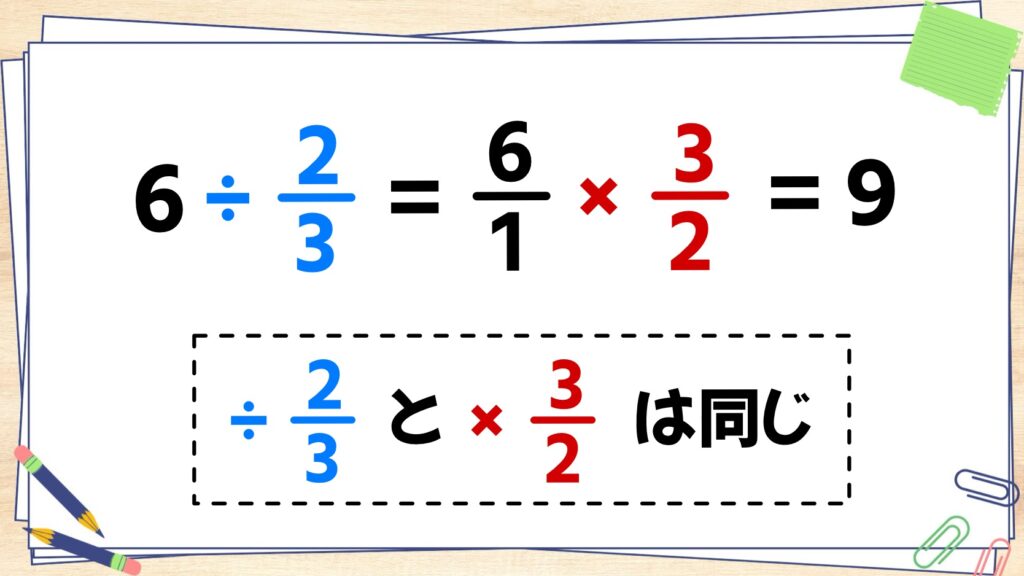
６に何をしたら９になるかを考えると、６×３/２＝９となることが分かるので、

÷２/３と×３/２は同じ

ということが言えますね。

無料資料請求はこちら↑↑↑

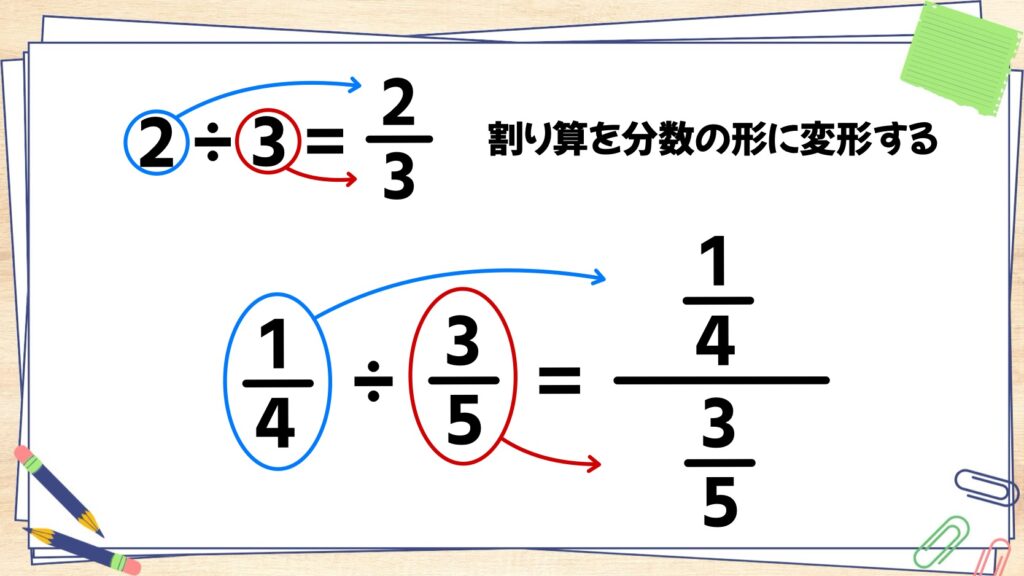
「割り算→分数」の変型で考える

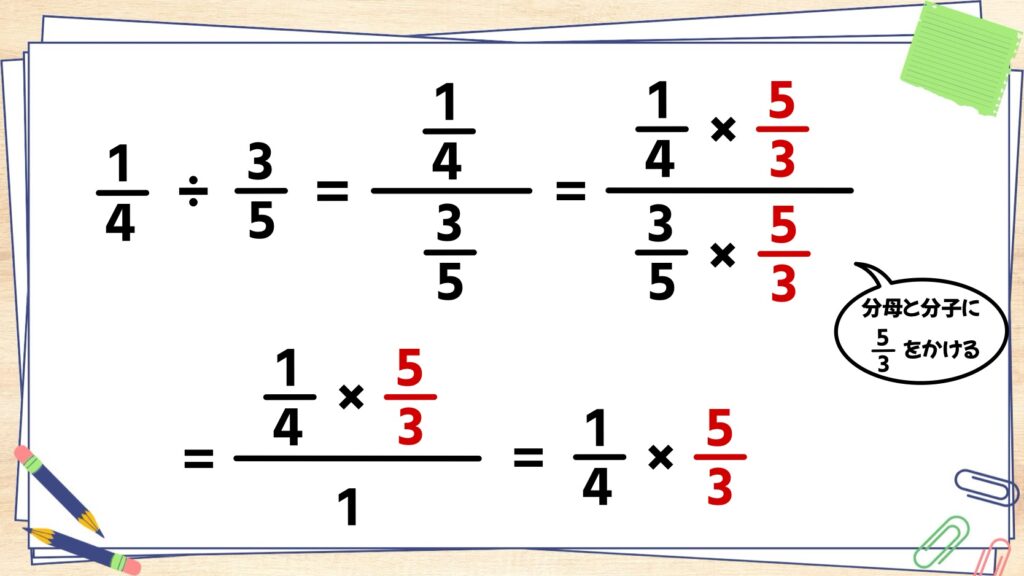
２÷３＝２/３のように、割り算は分数に変形することができます。これを分数の割り算で考えてみましょう。

１/４÷３/５を分数の形に直してみると、下の図のように変形することができます。この「分数の分数」の形を「繁分数」といいます。

分数は、分母と分子に同じ数をかけても数が変わらないという性質があります。この性質を使って、１/４分の３/５の分母と分子にそれぞれ５/３をかけます。

計算すると、分母が１になり、分子が１/４×５/３となります。

結果的に、１/４÷３/５=１/４×５/３

分数の割り算は中学校でも使う

「分数の割り算なんて、将来使わないでしょ？」と思う子どももいますが、実は中学校の数学では当たり前のように登場します。

例えば、方程式を解くときには分数を含んだ計算が出てきますし、比例・反比例の学習でも分数の計算を使います。また、文字式や関数の単元でも分数の割り算が必要になる場面は少なくありません。

中学校の数学でつまずく子どもの中には、小学校で学習した分数の計算が十分に身についていないケースも多く見られます。

そのため、小学校のうちに「なぜひっくり返してかけるのか」を理解しておくことは、単にテストで点数を取るためだけではなく、中学校以降の数学をスムーズに学ぶためにもとても大切です。

↓[授業準備を０にする】小６算数授業テンプレートをnoteで販売しています。　

まとめ

計算方法を覚えることも大切ですが、その理由まで理解できると、分数に対する理解はぐっと深まります。特に分数は、頭の中で量をイメージしながら考えることが重要な単元です。

今回紹介したように、図を使って考えたり、分数の性質を利用して考えたりすると、「逆数をかける理由」を納得して理解することができます。

また、分数の計算は中学校の方程式や関数、文字式などにもつながる大切な学習内容です。小学校のうちに「なぜそうなるのか」を理解しておくことで、中学校の数学もスムーズに学べるようになります。

ぜひ計算方法だけを暗記するのではなく、「なぜ？」を大切にしながら、分数の考え方そのものを理解していきましょう。

ブログ

三角形の内角の和が180°になることの解説！小中学生むけにイラストで分かりやすく

2024年7月7日

ブログ

【おうぎ形の公式】面積・弧の長さ・中心角の求め方をイラストで分かりやすく解説！

2024年6月24日

ブログ

０「ゼロ」と０「レイ」の違いを分かりやすく解説！数字の雑学

2024年6月8日

投稿者プロフィール

hiro先生: 教育×ICTクリエイター｜教育メディア運営
教員15年→2026/3退職中学数学13年＋小6算数専科2年
Apple Teacher・Kahoot!認定クリエイター
書籍「算数から数学への壁」（エール出版社）
授業で使える算数・数学問題、思考力を育てるクイズ、ICT活用法を発信。
これまでに5種類の兼業を経験し、ストック型副業で月10万円の収益を構築。
電子書籍「論理的思考問題５０」はAmazonベストセラー第７位を獲得。
現在は教育コンテンツ制作、デジタル教材開発、教員の働き方や副業について発信中。
SNS総フォロワー数は約3万人。