【小学生も分かる】分数の足し算と引き算はこう教える！図と例でやさしく解説

分数の足し算や引き算は、多くの子供がつまずきやすい単元の１つです。

特に通分をする必要がある”分母が違うときの計算”は、大人でも説明に悩むことがありますよね。

この記事では、分数の足し算・引き算の基本的な教え方を、図や具体例を使って分かりやすく解説をします。このページにある画像を保存して、そのまま子どもたちに見せて説明することもできます。

なぜ分数の計算でつまずくのか？

分数の足し算や引き算でつまずく理由の１つは、分数を足したり引いたりするイメージが持ちにくいからです。

例えば３ー２という問題であれば、「３個のリンゴから、２個食べたら残りは何個？」というイメージを頭の中ですぐに描くことができますが、「２/３ー１/３」という問題になると、なぜ分母同士は計算をしなのか、なぜ分子だけを計算をするのかなど、イメージをすることが難しくなります。

更に分母の数字が違う「１/２＋１/３」という計算となると、なぜそのまま計算してはいけないのか？なぜ通分しなくてはいけないのか？より子どもを混乱させてしまいます。

どちらも、”イメージしにくい”ということが、つまずく原因となるので、視覚的に子どもの理解を促すことが重要になります。

通分はなぜ必要なの？

分数の計算で多くの子どもが疑問に思うのが、「なんで通分しないといけないの？」ということです。

例えば、1/2 + 1/3という計算を見て、「1+1で2、2+3で5だから2/5！」と考えてしまう子はとても多いです。

しかし、これは間違いです。なぜなら、1/2と1/3は大きさの基準が違うからです。

例えば、

• 1メートル
• 50センチメートル

を足すときに、「1＋50＝51」とは計算しませんよね。

まずは、1メートル＝100センチメートルに直して、100cm＋50cm＝150cmと、単位をそろえてから計算します。

分数もこれと同じです。1/2は「2つに分けたうちの1つ」、1/3は「3つに分けたうちの1つ」なので、分け方が違います。

そのままでは足し算や引き算ができません。そこで、1/2＝3/6、1/3＝2/6のように、どちらも「6つに分けたうちの何個分か」にそろえます。これが通分です。

通分をすると、3/6＋2/6＝5/6と計算できるようになります。

つまり、通分とは、「分数の大きさを変えずに、分け方をそろえる作業」なのです。

子どもには、「分数の通分は、長さをメートルとセンチメートルでそろえるのと同じだよ」と説明すると、とても理解しやすくなります。

分数の基本をしっかり押さえよう

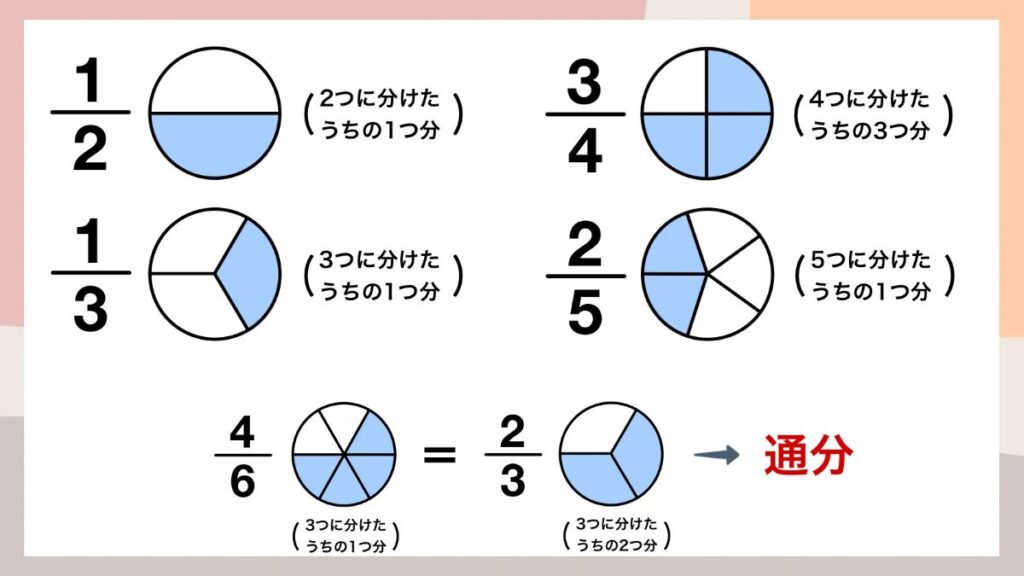
まずは分数の基本的な概念をしっかりと押さえましょう。

大切なのは、分数は「１つのものを”何個に分けたうちの何個分か”を表している」ということです。たとえば、「１/２」は、「１つのケーキを、”２個に分けたうちの１つ分”」という意味になります。

また、「同じ分母の分数同士しか、足したり引いたりできない」というルールもポイントです。分母の違う分数の場合は、分数の大きさを揃える、”通分”をする必要があります。

分母が同じときのたし算とひき算

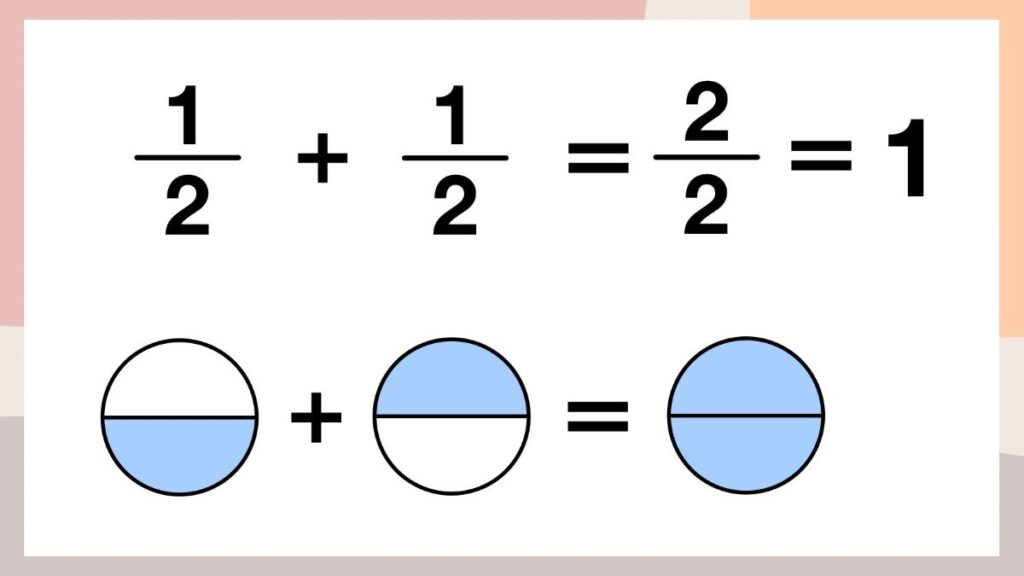
１/２＋１/２→「２つに分けたうちの１つ分」と「２つに分けたうちの１つ分」を足すと、「２つに分けたうちの２つ分」となり、１になります。

１/３＋１/３→「３つに分けたうちの１つ分」と「３つに分けたうちの１つ分」を足すと、「３つに分けたうちの２つ分」となり、２/３になります。

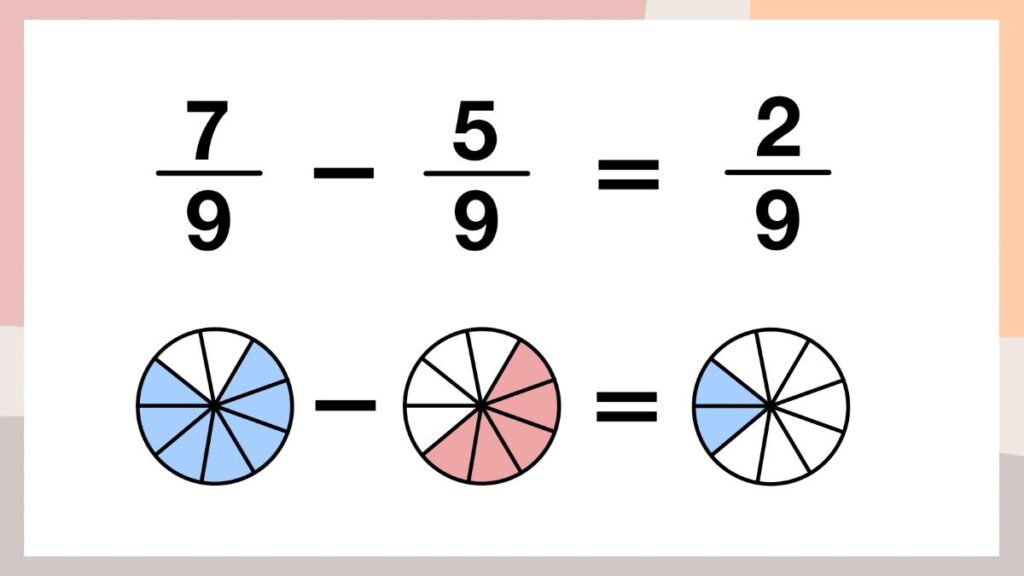
引き算のときも同じように考えます。

７/９－５/９→「９つに分けたうちの７つ分」から「９つに分けたうちの５つ分」を引くと、「９つに分けたうちの２つ分」となり、２/９となります。

分母が同じ数字の場合は、比較的簡単にイメージすることができます。

分母が違うときはどうする？

分母が違うときはどうでしょうか？

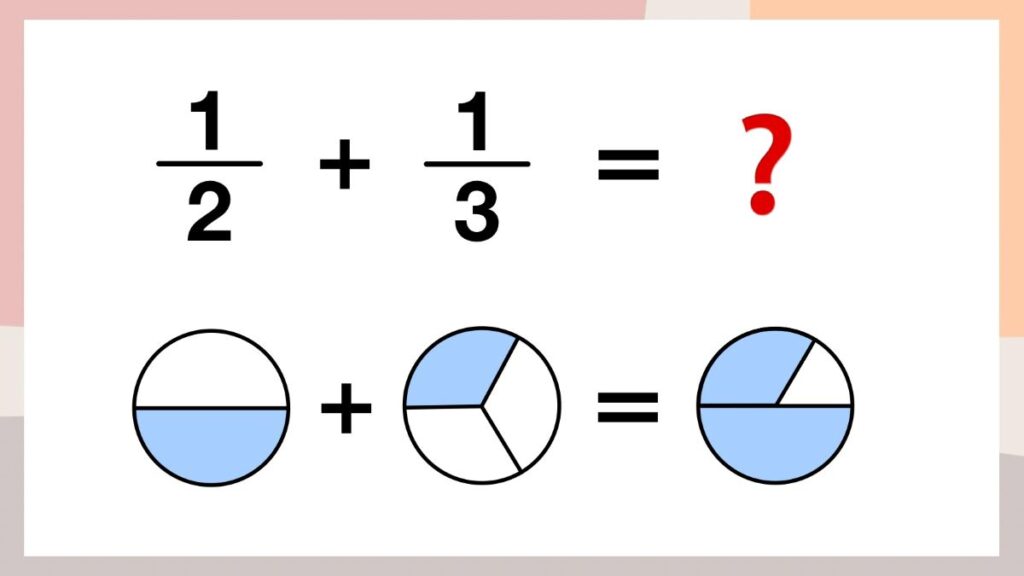
よく、「分母の違う分数は足すことができない」と教わったことがある人がいるかもしれませんが、それは正確ではありません。

実際には１/２＋１/３のような、違う分母の分数を足すと画像のようになります。

足すことはできても数字で表すことが難しいので、通分をします。

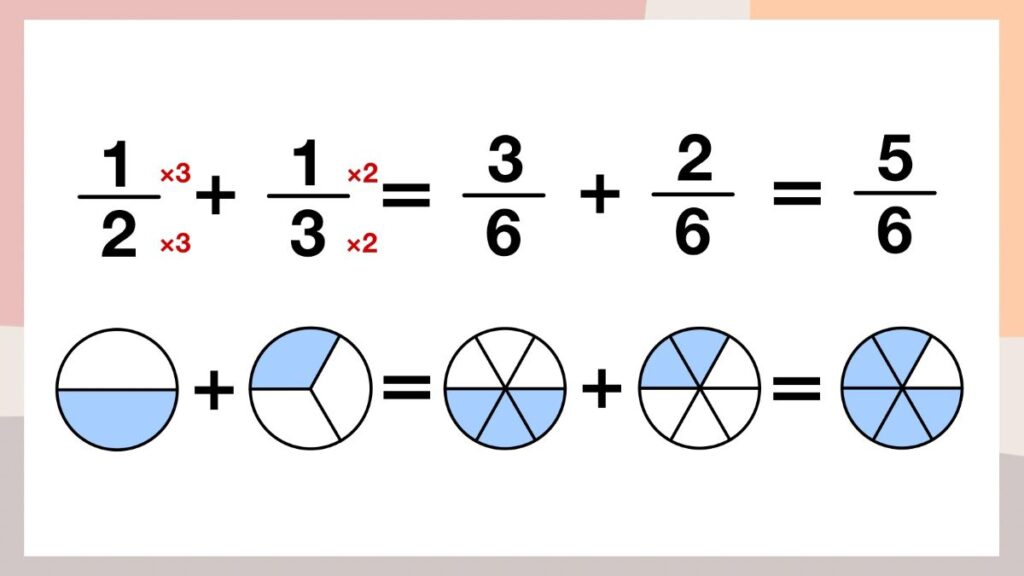
「２つに分けたうちの１つ」を「６つに分けたうちの３つ」とし、「３つに分けたうちの１つ」を「６つに分けたうちの２つ」とします。

「６つに分けたうちの３つ」と「６つに分けたうちの２つ」を足すと、「６つに分けたうちの５つ」となります。

これを数字で表すと１/２＋１/３＝３/６＋２/６＝５/６となります。

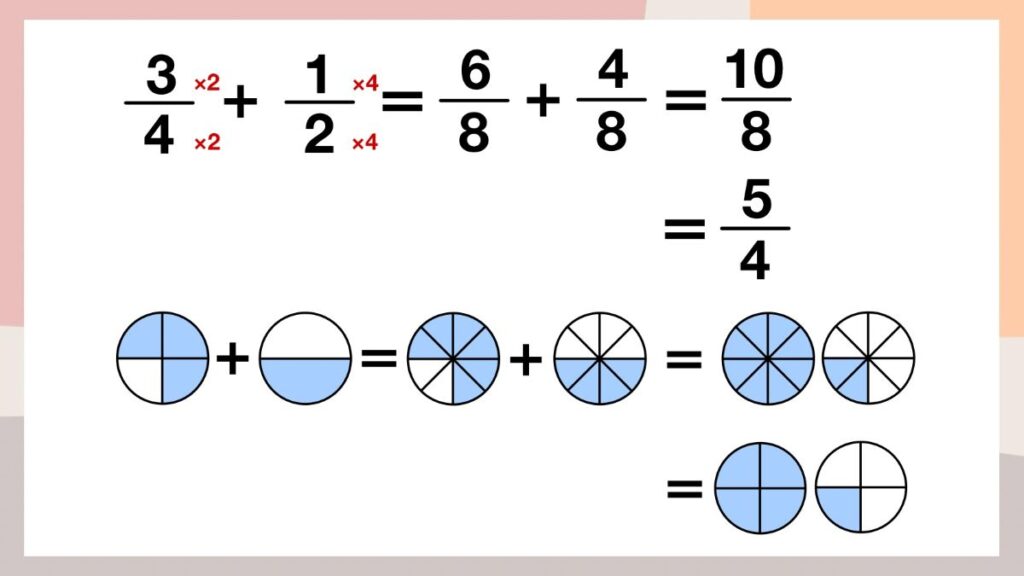
別の例で見てみましょう。

「４つに分けたうちの３つ」を「８つに分けたうちの６つ」とし、「２つに分けたうちの１つ」を「８つに分けたうちの４つ」とします。

「８つに分けたうちの６つ」と「８つに分けたうちの４つ」を足すと、「８つに分けたうちの１０個」となります。

これを数字で表すと３/４＋１/２＝６/８＋４/８＝１０/８＝５/４となります。

分数の足し算を教えるときのコツ

分数の足し算や引き算を教えるときに大切なのは、いきなり計算方法を覚えさせないことです。

子どもは「分母はそのまま」「通分する」といったルールだけを覚えても、意味が分からなければすぐに忘れてしまいます。

まずはケーキやピザ、テープ図などを使って、「どれくらいの大きさなのか」をイメージさせましょう。

また、1/3を「3分の1」と読むだけでなく、「3つに分けたうちの1つ分」と説明することも大切です。この言葉を繰り返すことで、分数の意味を理解しやすくなります。

例えば、

1/3＋1/3＝2/3

であれば、「分子を足したから」ではなく、「3つに分けたうちの1つ分が2個になったから」と説明できる状態を目指したいところです。

分数の学習では、計算方法を覚えることよりも、「なぜそうなるのか」を理解することが重要です。図や具体物を使いながら、子どもが「なるほど！」と思える授業を心がけましょう。

まとめ

分数の足し算や引き算は、多くの子どもが苦手にしやすい単元ですが、その原因の多くは「計算方法は覚えたけれど、意味が分かっていない」ことにあります。

大切なのは、いきなり通分や計算のルールを教えるのではなく、「何個に分けたうちの何個分なのか」を図や具体物を使ってイメージさせることです。

特に通分は、分数の大きさをそろえるための作業だと理解できると、子どもは納得しながら計算できるようになります。

分数は小学校だけでなく、中学校以降の数学でも何度も登場する大切な内容です。ぜひ図を活用しながら、「なぜそうなるのか」を大切にして教えてあげてください。きっと子どもたちの理解が深まり、分数への苦手意識も減っていくはずです。

投稿者プロフィール

hiro先生

教育×ICTクリエイター｜教育メディア運営
教員15年→2026/3退職 中学数学13年＋小6算数専科2年
Apple Teacher・Kahoot!認定クリエイター
書籍「算数から数学への壁」（エール出版社）
授業で使える算数・数学問題、思考力を育てるクイズ、ICT活用法を発信。
これまでに5種類の兼業を経験し、ストック型副業で月10万円の収益を構築。
電子書籍「論理的思考問題５０」はAmazonベストセラー第７位を獲得。
現在は教育コンテンツ制作、デジタル教材開発、教員の働き方や副業について発信中。
SNS総フォロワー数は約3万人。

最新の投稿

• ブログ2026年8月5日学校で使えるアイスブレイク10選｜学級開き・新学期におすすめのレク
• ブログ2026年8月4日先生はみんなAppleTeacherになろう！メリットと取得方法を紹介！
• ブログ2026年8月3日【世界のあいさつクイズ20問】何語の言葉か当てる4択問題 
• ブログ2026年8月2日【三字熟語パズル15問】バラバラの漢字を組み合わせる言葉クイズ