葉っぱ型（レンズ型）の面積の求め方と裏技0.57！算数の不思議を解説！

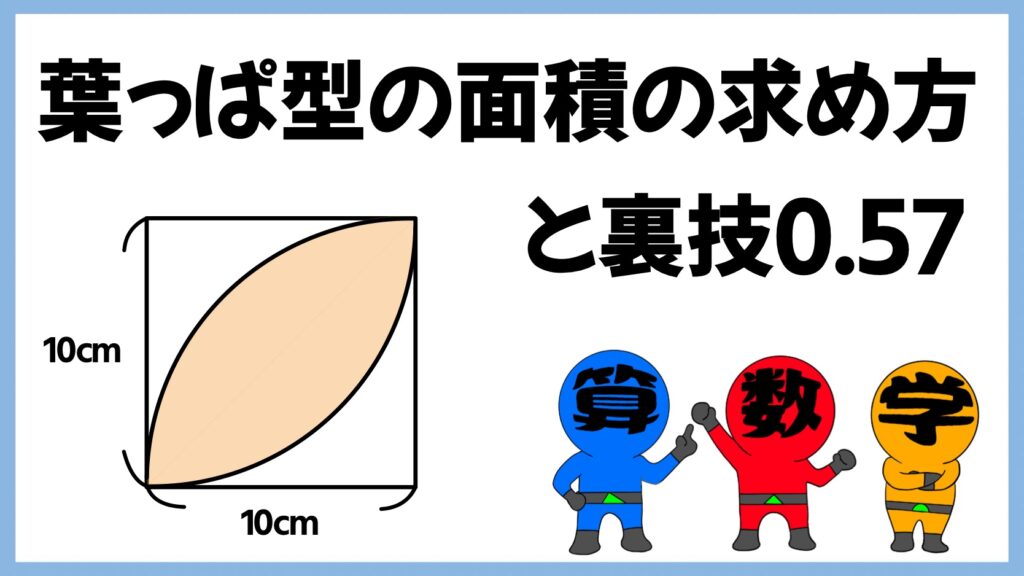
今回は「葉っぱ型」や「レンズ型」と呼ばれる、おうぎ形を組み合わせた形の面積の求め方と、「正方形の面積×0.57」の裏技について解説をしていきたいと思います！

　面積を求める基本的な考え方

一般的に図形の面積を求める時には、次のような順序で考えます。

１．図形の種類を確認する

　最初に与えられた図形が何であるかを確認します。長方形、三角形、円、または複雑な図形であれば、基本的な図形に分割できるかを考えます。

２．公式を使う

　公式が使える図形であれば、適切な公式を使います。例えば、長方形であればタテ×ヨコ、三角形なら底辺×高さ÷２などです。

３．複雑な図形は分割して考える

　複雑な図形は、基本的な形に分割してそれぞれの面積を求められるか考えます。例えば、L字型の形ならば２つの長方形に分けてそれぞれの面積を足し合わせることで求めることができます。

４．引き算を使う場合もある

　今回ご紹介する「葉っぱ型」の面積を求める場合も、引き算を使うことが一般的です。求められる形の面積同氏を引くことによって、公式では求められないような図形の面積を求めることができます。

　葉っぱ型の面積の求め方

「葉っぱ型」の図形は、中心角が90°のおうぎ形２つを組み合わせた図形で、「木の葉型」「ラグビーボール型」「レンズ型」など、様々な呼び方があります。

ここからは面積の求め方の考え方を、１辺が10㎝の正方形を使って４種類ご紹介します。

　考え方①

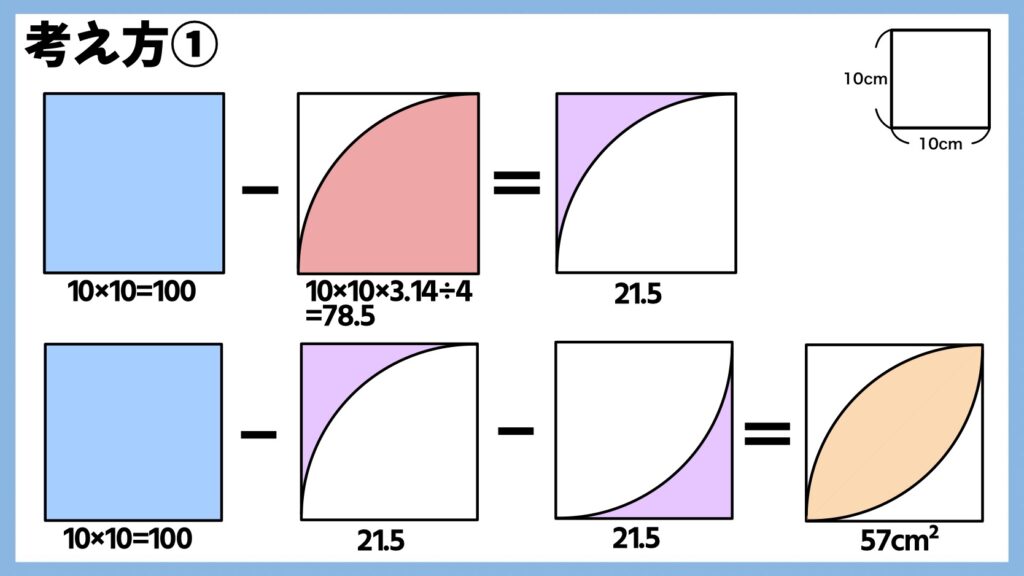
正方形の面積から中心角９０°の扇形の面積を引くと

（１０×１０）ー（１０×１０×３．１４÷４）＝２１．５

となり、紫の図形の面積を求めることができます。

元の正方形から、この２つの紫の図形の面積を引くと

１００－２１．５ー２１．５＝５７

となり、「葉っぱ型」の面積を求めることができました。

　考え方②

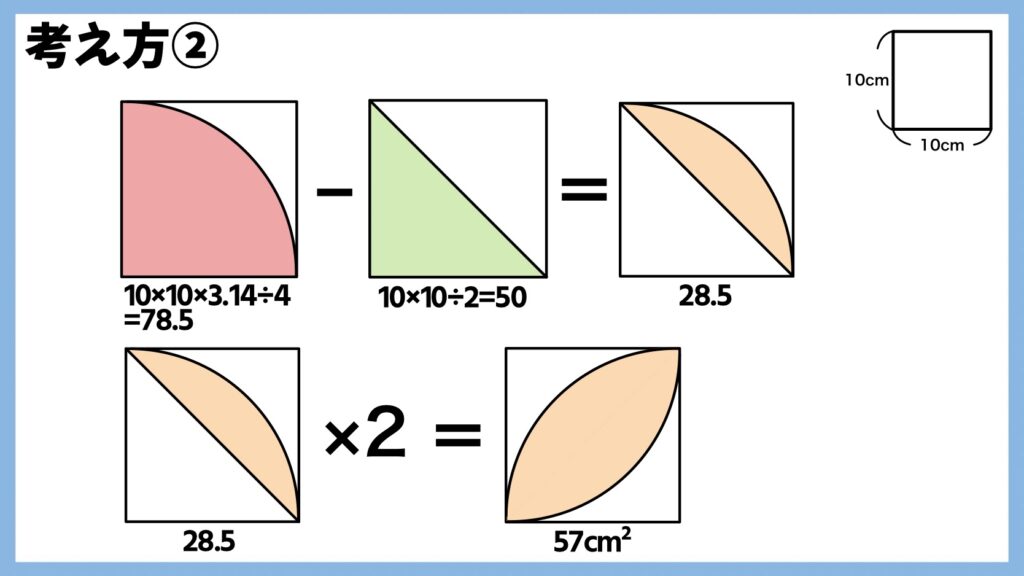
中心角９０°のおうぎ形から正方形の半分の直角三角形の面積を引くと

（１０×１０×３．１４÷４）－（１０×１０÷２）＝２８．５

となり、三日月型のような形をした図形の面積を求めることができます。この三日月形の面積を２倍すると

２８．５×２＝５７

となり、「葉っぱ型」の面積を求めることができました。

　考え方③

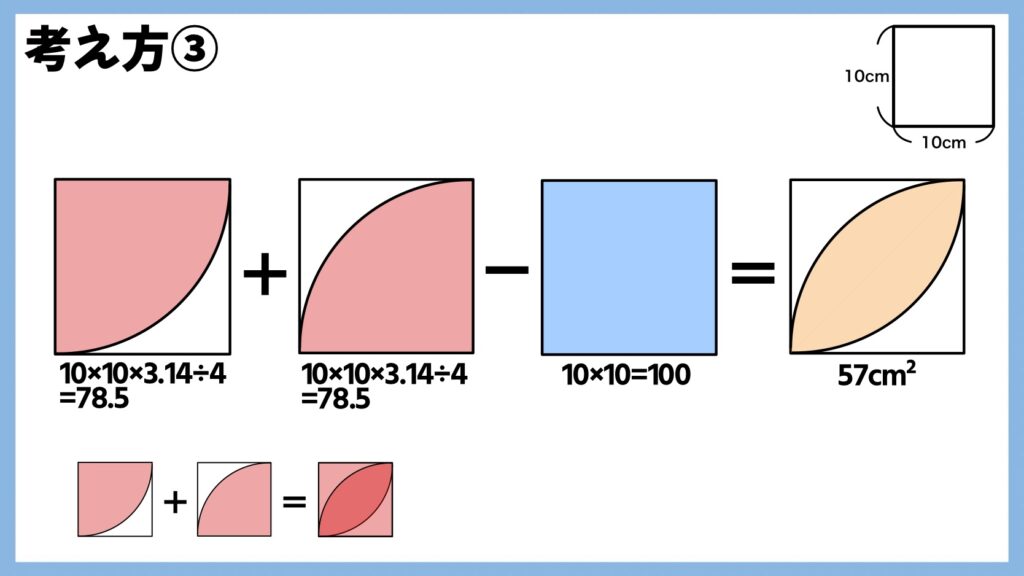
中心角が９０°のおうぎ形を２つ重ねると、「葉っぱ型」部分が２重になります。そこから正方形の面積を引くと

（１０×１０×３．１４÷４）＋（１０×１０×３．１４÷４）－１００＝５７

となり、「葉っぱ型」の面積を求めることができました。

　考え方④

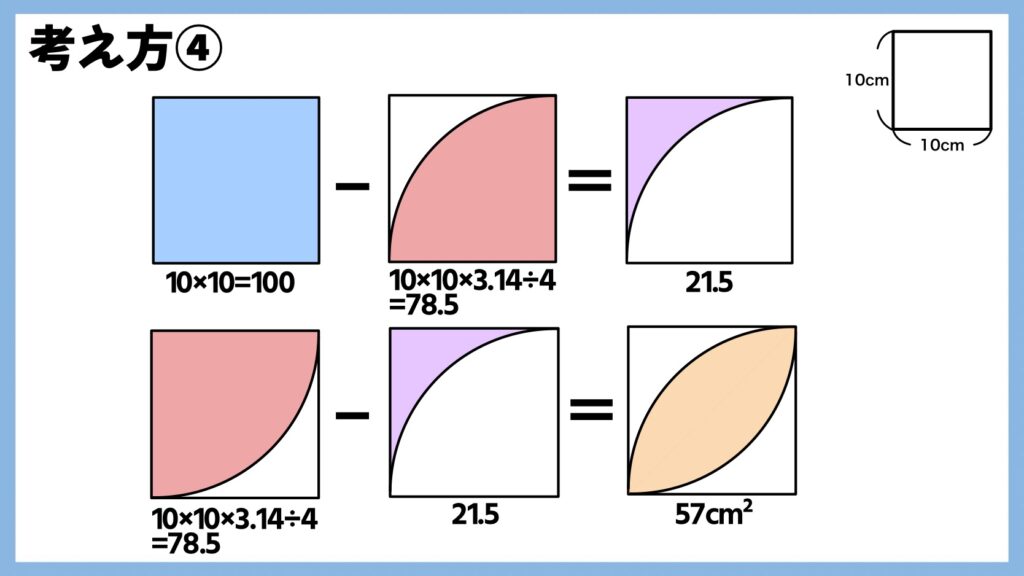
考え方①のように、正方形の面積から中心角９０°の扇形の面積を引きます

（１０×１０）ー（１０×１０×３．１４÷４）＝２１．５

そして中心角９０°の扇形の面積から求めた紫の面積を引くと

（１０×１０×３．１４÷４）ー２１．５＝５７

となります。

　裏技

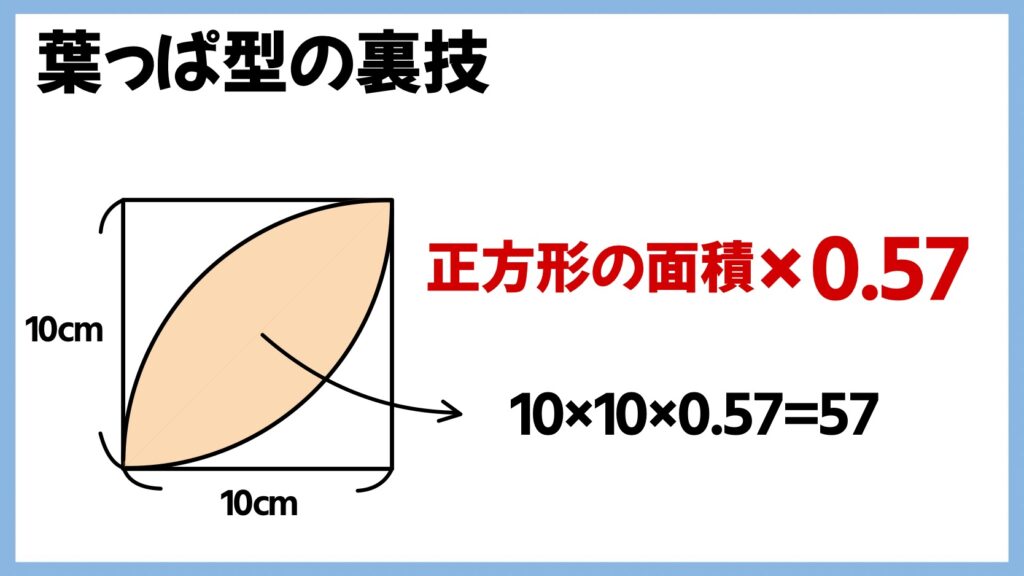
　なぜ「正方形の面積×0.57倍」？

なんで０．５７倍になるの？と疑問を持つ人も多いでしょう。僕も子供に教えていて、「なんで０．５７なの！？」とよく質問をされました。

１辺が１㎝の正方形と、１辺が２㎝の正方形を使って説明します。

画像左のように、１辺が１㎝の正方形の面積は１cm²となります。中心角が90°のおうぎ形は０．７８５cm²、三角形は０．５cm²、三日月型は０．２８５cm²、「葉っぱ型」は０．５７cm²となり、それぞれ正方形の面積の０．７８５倍、０．５倍、０．２８５倍、０．５７倍となります。

画像右の１辺が２㎝の正方形の面積は２cm²で、中心角が90°のおうぎ形は３．１４cm²、三角形は２cm²、三日月型は１．１４cm²、「葉っぱ型」は２．２８cm²となり、それぞれ正方形の面積の０．７８５倍、０．５倍、０．２８５倍、０．５７倍となることが分かります。

つまり「葉っぱ型」の面積は、１辺の長さに関係なく「正方形の面積×０．５７」になるというわけです。

　裏技の注意点

ここまで解説した通り、葉っぱ型の面積は「正方形の面積×0.57」で求めることができるのですが、これは公式っぽい”裏技”であることを忘れてはいけません。

中学受験などの入試問題ではほとんどの場合、円周率は3.14と指定されていますが、まれに3.1、や22/7など、3.14ではない場合があります。

円周率が3.14ではない場合、この「正方形の面積×0.57」は使えないということを知っておかなければいけません。つまり、無条件で使える公式とは違い、便利に使うことができるため「裏技」と言われています。

　よく出る応用問題

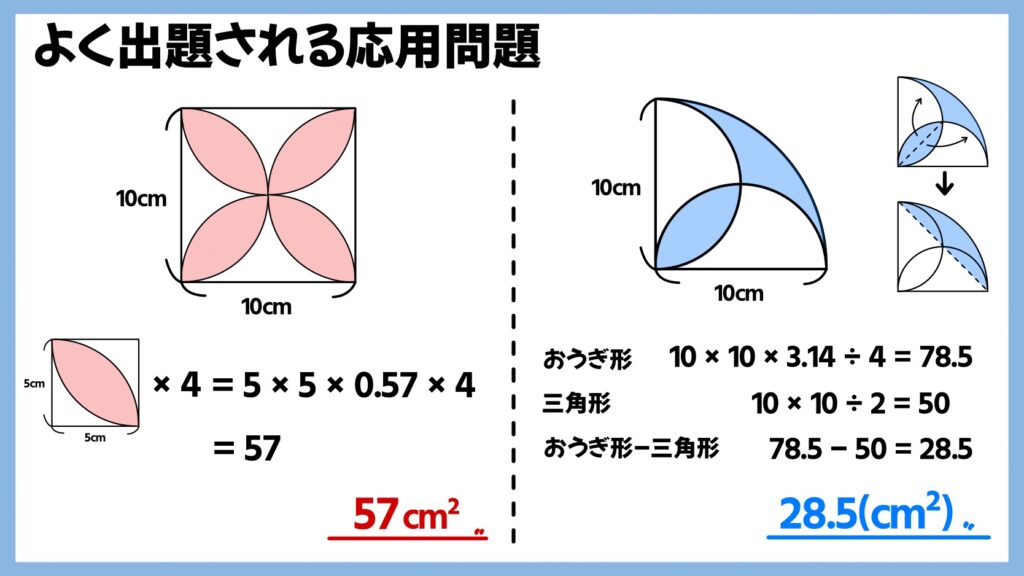
中学受験などでよく出る応用問題を２種類ご紹介します。

画像左の問題は、花びら型などと呼ばれる形の図形です。ここまで解説した「葉っぱ型」の面積の求め方が分かっていれば、１つの「葉っぱ型」を４倍するだけで答えが出ることが分かると思います。

画像右の弓のような形の問題は少し工夫が必要です。真ん中の「葉っぱ型」を半分に分けて組み合わせると、おうぎ形の面積ことから三角形の面積を引いた図形になります。

　まとめ

いかがだったでしょうか？

今回はおうぎ形を２つ組み合わせた「葉っぱ型」の面積の求め方と裏技「正方形の面積×０．５７」を解説しました。

どんな時でも無条件に使える、「公式」ではなく「裏技」であることに注意してください。円周率が３．１４であるときのみ使える便利な裏技を使って、サクサク問題を解いちゃいましょう！