結論から言うと、計算する順番を決めておかないと、人によって答えが変わってしまうからです。
小学校で計算の順番を学習すると、「なんでかけ算を先に計算するの？」と疑問に思う子どもがいます。
確かに、何も知らなければ左から順番に計算した方が自然に感じるかもしれません。
結論から言うと、計算する順番を決めておかないと、人によって答えが変わってしまうからです。
もし計算の順番が決まっていなかったら、同じ問題なのに答えが2通り出てしまうことがあります。
算数や数学では、誰が計算しても同じ答えになることがとても大切です。
そのため、
（ ）→ ×・÷ → ＋・－
という共通のルールが決められています。
この記事では、なぜかけ算やわり算を先に計算するのかを、小学生にも分かるように身近な例を使いながら解説していきます。
「ルールだから覚えよう」ではなく、「なぜそのルールが必要なのか」を理解しよう！
【RISU算数のレビューと口コミ】現役数学教師がタブレット学習教材を使ってみた！
なぜ円周率は３．１４なのか？求め方を分かりやすく紹介！
分数の割り算はなぜひっくり返す？逆数をかける理由を解説！
結論：答えが複数出てしまうから
かけ算やわり算を先に計算する理由は、「ルールがないと答えが複数出てきてしまうから」です。
かけ算やわり算から計算しなければいけないという数学的な決まりはないみたいですが、ある一定の決まりがなければ、答えが２つ出てきてしまうような問題が存在します。
つまり、かけ算やわり算を先に計算すると決めておかないと答えの食い違いが生じてしまうからです。
１０－４×２を考える
ここで１０－４×２という問題を考えてみましょう。
もし左から順番に計算した場合、１０－４＝６を先に計算し、６×２＝１２という答えになりますね。
一方でかけ算を先に計算した場合は、４×２＝８を先に計算し、１０－８＝２という答えになります。
同じ計算でも答えが二つ出てきてしまいましたね。解く人によって答えが違ってしまったら困りますよね。
ではなぜ、たし算やひき算ではなく、かけ算とわり算を先に計算することになったのか、下の単位の違いで説明してみましょう。
単位の違いで考える
例えば、「１００円のお菓子３つと１２０円のジュースを買った代金の合計は？」という問題があったとします。
式にすると”１００×３＋１２０”となり、小学校３年生くらいで習う計算式になります。
単位を付けてみると”１００円×３個＋１２０円”
この計算式を”３個＋１２０円”を先に計算するのは式の意味合いからするとおかしいことが分かりますね。
「１００円お菓子を３個買った代金」と「１２０円のジュースの代金」の合計を求めなくてはいけないので、かけ算から先に計算することになります。
わり算とかけ算の計算は左から
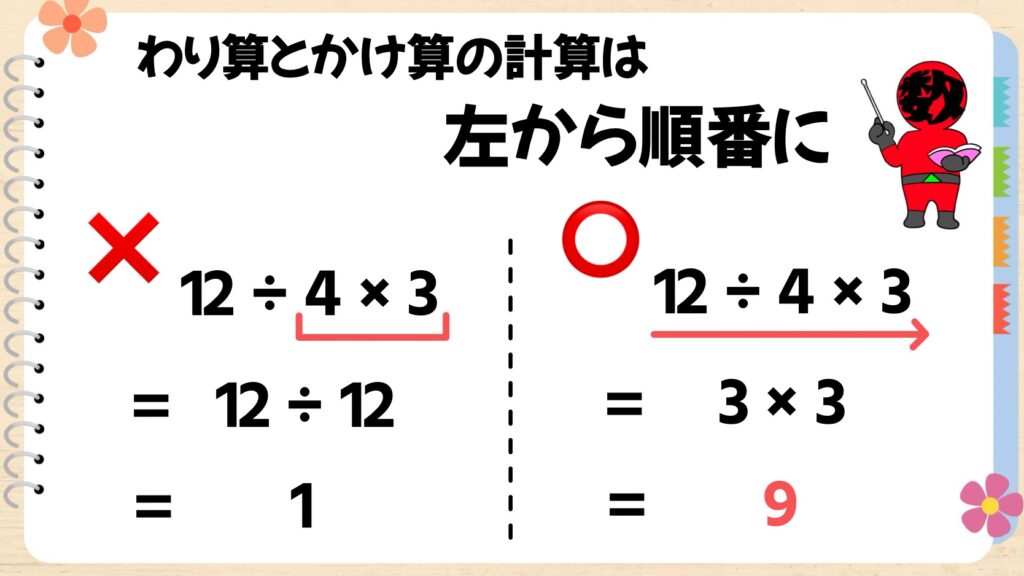
「かけ算とわり算の式では左から順番に計算する」という決まりがあります。これも、答えが複数出てきてしまうからという理由です。
「１２個のケーキを４人で分けることを３回繰り返したら、１人何個ケーキを食べられる？」という問題考をえてみると、１２個のケーキを４人で分ける時点で１人３個は食べられるはずなのに、答えが１になるのはどう考えてもおかしいですよね。
４×３を先に計算してしまうと、１２個のケーキを１２人で分けることになっていまい、問題の意味とは大きく変わってしまいます。
他にもこんなことができる
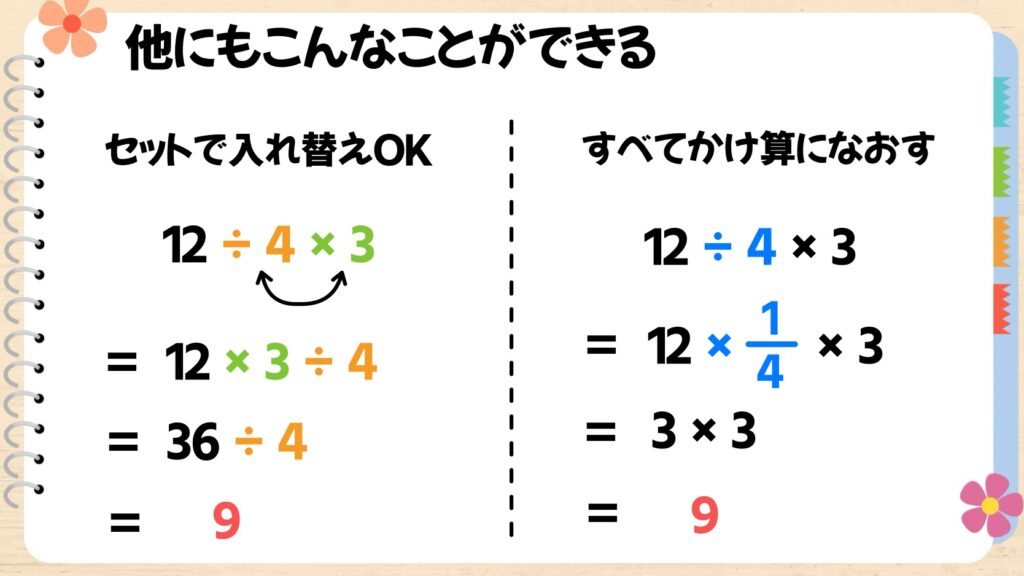
「÷４」と「×３」の計算記号をセットで入れ替えることができます。
先ほどの問題で考えると、「１２個入りのケーキ３箱を、４人で分けたら１人何個ケーキを食べられる？」という意味となり、答えは３６÷４＝９となります。
また、わり算をかけ算に直してから計算する方法もあります。
中学生への繋がり
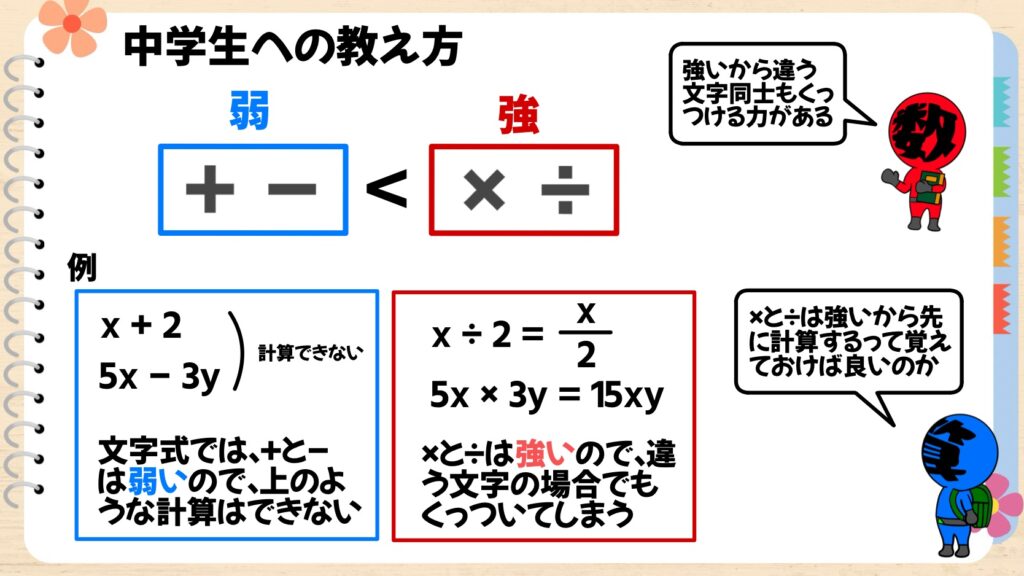
僕は中学生には「たし算ひき算とかけ算わり算には強弱がある」ということを教えています。（あくまでイメージの世界ですが）
中学１年生の数学では文字の式という単元で、小学校ではやらなかった、かけ算の省略や文字を使ったわり算が登場します。
例えば”ｘ＋２”や”５ｘー３ｙ”などの、文字が違う場合のたし算やひき算は計算ができません。なぜならば、「＋と－はくっつける力が弱い」からです。
一方”ｘ÷２”や５ｘ×３ｙ”は、それぞれｘ/２、１５ｘｙとわり算は上下に、かけ算は前後にくっついてしまいます。「×と÷はくっつける力が強い」からです。
このように、＋と－、×と÷には明確に強さが違う。だから同じ式に＋と×がある場合は強い×から先に計算するということです。
議論を巻き起こした6÷2(1+2)
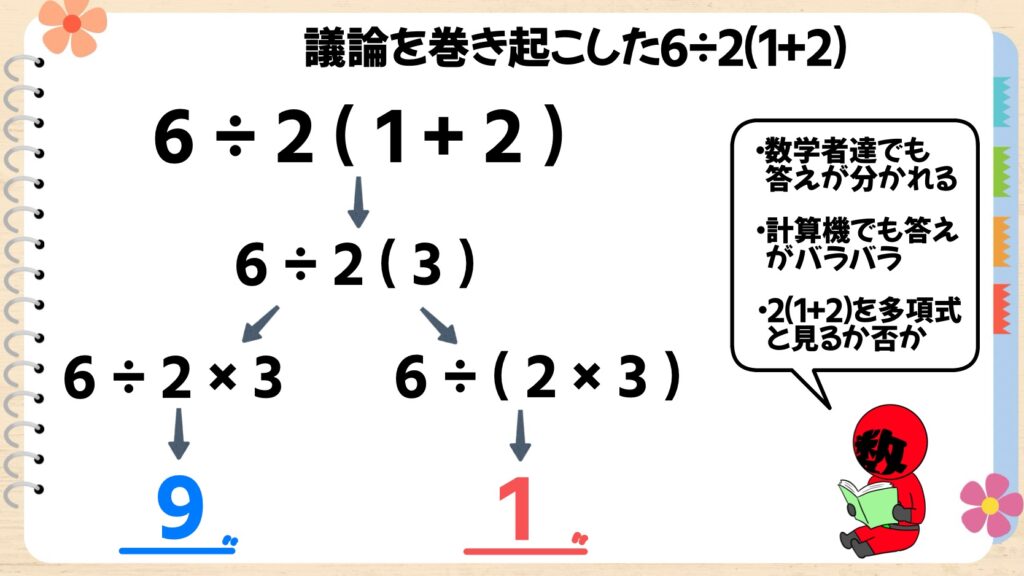
上の画像の問題は、SNS上で話題になった有名な問題です。
計算の順番としては、（ ）→×÷→＋－という順番になるので、まずは（１＋２）＝３から計算します。ここまでは誰でも分かります。
問題はそのあと、この計算を”６÷２×３”と考えるのか、６÷（２×３）と考えるのかで、数学者達の間でも答えが分かれてしまいました。また、電卓で計算しても、メーカーによって答えが２通り出てくるというのだから驚きですよね。
２（１＋２）を１つの塊（多項式）としてみるかどうかで答えが変わってしまうということです。
この式の問題点は、通常普通の計算では省略しない×を省略してしまったことから、このような話題になるに至ったそうです。
計算のルールは未だに完ぺきではないのかもしませんね！
計算の順番で子どもがつまずく理由
計算の順番は小学校で学習しますが、意外と苦手な子どもが多い問題でもあります。
その理由の一つは、子どもが「左から順番に計算したい」と考えるからです。文章を読むときも、計算するときも左から進めることが多いため、自然な感覚としては間違っていません。
「かけ算やわり算を先に計算する」というルールを覚えても、かけ算とわり算はとっちが先？（ ）カッコがある場合は？
さらに、式の意味を考えずに計算だけをしてしまうことも原因です。例えば「100円のお菓子を3個買う」という場面では、先に100×3を計算しなければ意味が通りません。式は単なる数字の並びではなく、実際の場面を表していることを理解することが大切です。
だからこそ、計算の順番は暗記するのではなく、「なぜその順番なのか」を考えながら学習することが重要なのです。
まとめ
いかがだったでしょうか？
かけ算やわり算を先に計算する理由は、計算する人によって答えが変わってしまうことを防ぐためです。
もし計算の順番にルールがなければ、同じ問題でも複数の答えが出てしまい、算数や数学が成り立たなくなってしまいます。
また、かけ算やわり算を先に計算することで、式が表している意味も正しく保つことができます。
大切なのは、「ルールだから覚える」のではなく、「なぜそのルールが必要なのか」を理解することです。理由が分かると計算の順番を忘れにくくなりますし、中学校の文字式や方程式の学習にもつながっていきます。
ぜひお子さんに質問されたときは、「そういう決まりだから」ではなく、「答えを一つに決めるためなんだよ」と説明してあげてくださいね。
葉っぱ型（レンズ型）の面積の求め方と裏技0.57！算数の不思議を解説！
【最小公倍数と最大公約数の求め方】イラスト付きで分かりやすく解説！
投稿者プロフィール
-
教育×ICTクリエイター｜教育メディア運営
教員15年→2026/3退職 中学数学13年＋小6算数専科2年
Apple Teacher・Kahoot!認定クリエイター
書籍「算数から数学への壁」（エール出版社）
授業で使える算数・数学問題、思考力を育てるクイズ、ICT活用法を発信。
これまでに5種類の兼業を経験し、ストック型副業で月10万円の収益を構築。
電子書籍「論理的思考問題５０」はAmazonベストセラー第７位を獲得。
現在は教育コンテンツ制作、デジタル教材開発、教員の働き方や副業について発信中。
SNS総フォロワー数は約3万人。
最新の投稿
ブログ2026年6月5日【小６算数】分数÷分数はどうやって教える？子どもに理解させるポイント解説- ブログ2026年6月2日【小６算数の授業】分を時間、秒を分になおす分数の教え方を解説
- ブログ2026年5月9日バスレク12選｜イラストで解説！小学生が大盛り上がりするゲームを紹介
- ブログ2026年5月6日学校シーン間違い探し５問｜子どもが夢中になる問題集
