
令和6年度(2024年度)大阪府の高等学校入学者選抜学力検査テスト、数学の問題を解説します!難易度の高いC問題も分かりやすく解説てますよー!
それではどーぞ!

どこよりも分かりやすく解説しているよ!
A問題 1,2


1
(1)正負の数の加法、減法(2)正負の数の乗法、除法(3)指数の計算
(4)文字式の計算(5)文字式の乗法(6)平方根の計算
2
(1)式の値の問題(2)数の大小の問題(3)不等式の立式
(4)連立方程式の問題(5)確率の問題
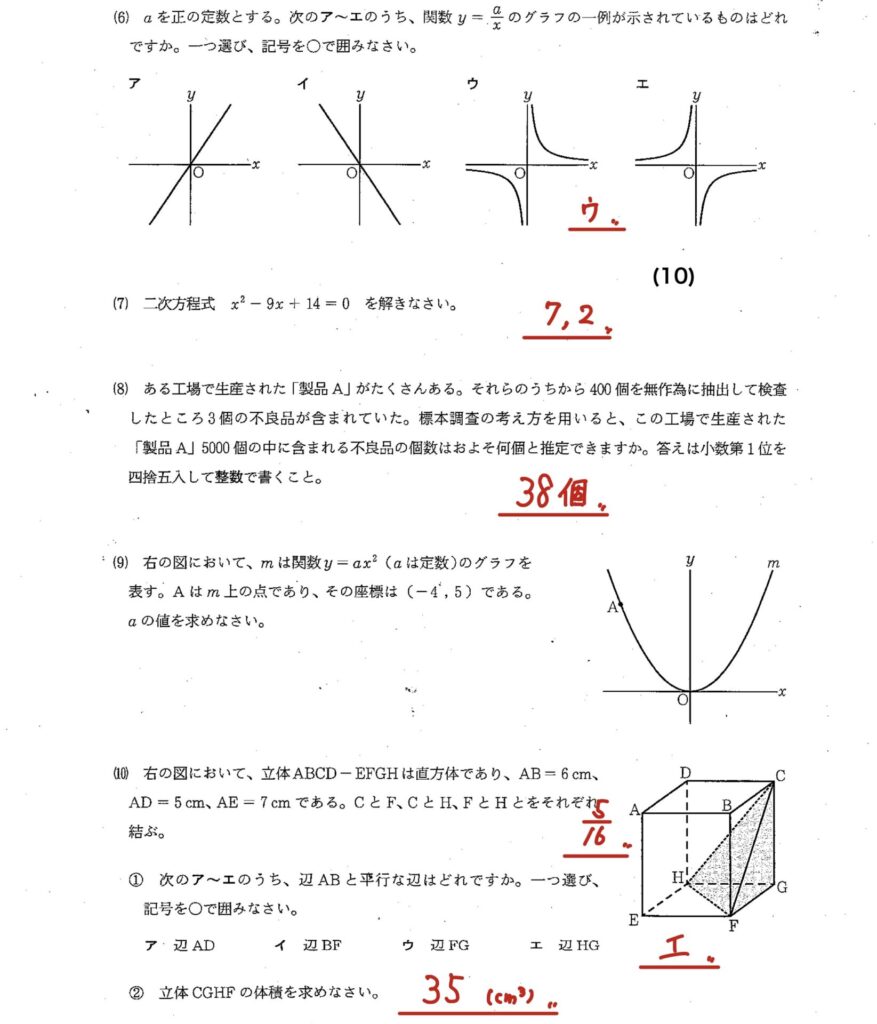

2
(6)反比例の式の問題
(7)二次方程式の問題
(8)比例式を使う問題
(9)関数y=ax²が(-4,5)を通るとき、aを求める
(10)直方体の中に三角錐がある。平行な直線と体積を求める問題
A問題 3
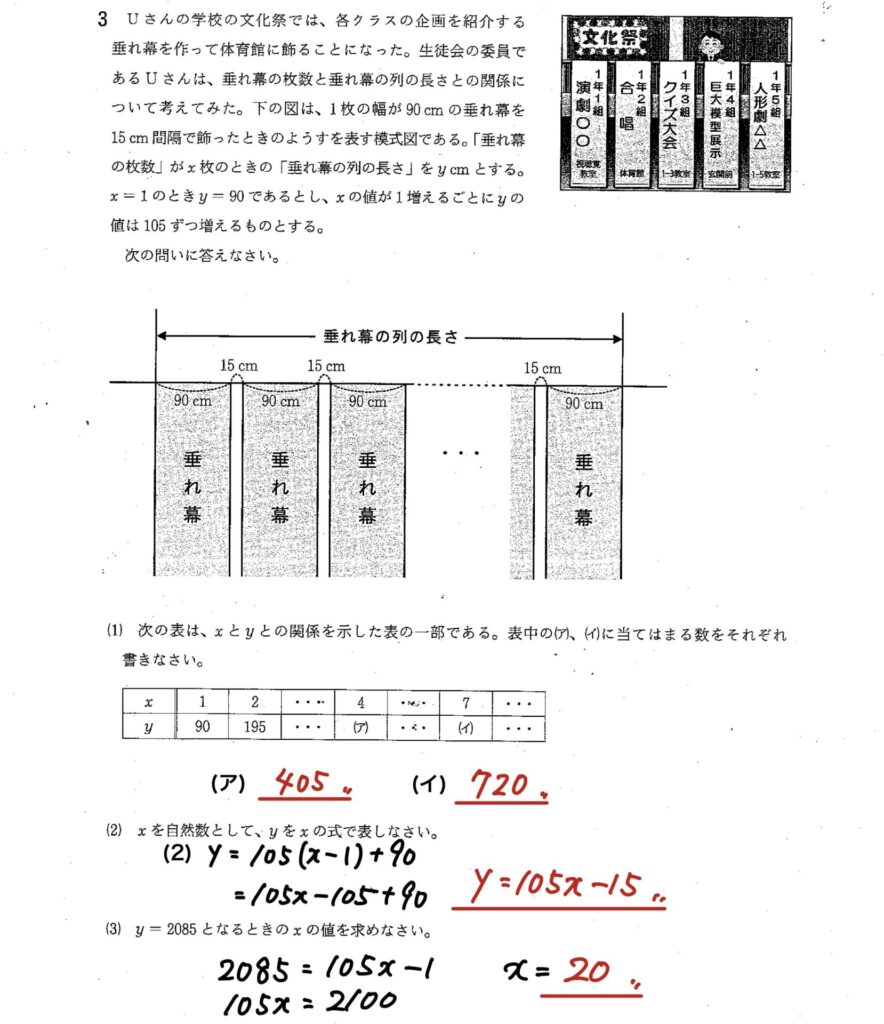
3
(1)一次関数の表をうめる問題
(2)一次関数の表から式を求める問題
(3)求めた一次関数の式にy=2085を代入してxの値を求める
A問題 4

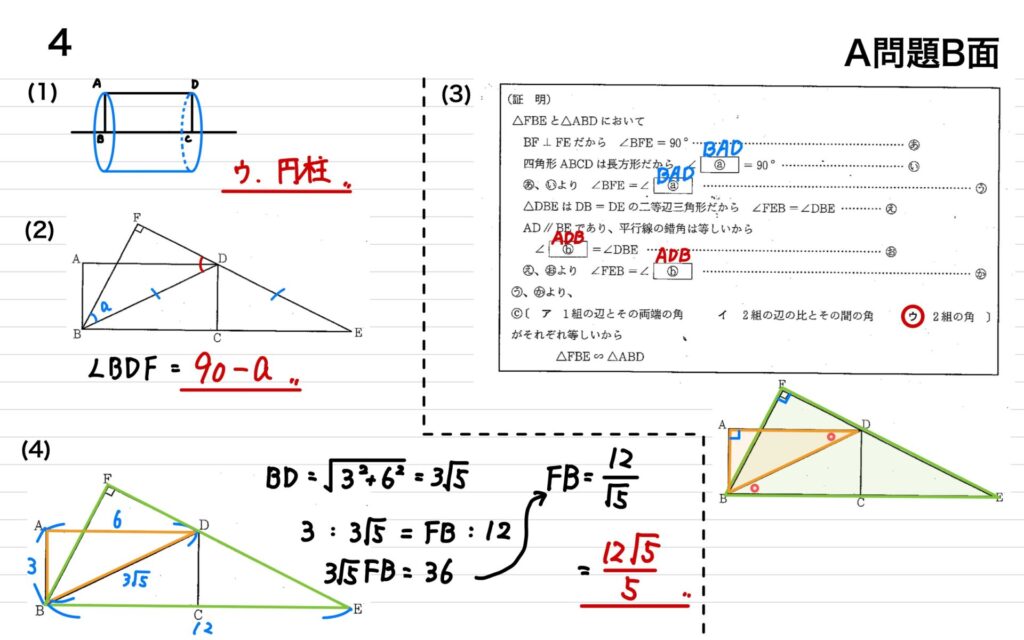
4
(1)長方形ABCDをBCを回転の軸として回転させたときにできる立体の名前を答える問題
(2)∠BDFをaを使って表す。△BDFは直角三角形なので、∠BDF=90ーaとなる
(3)△FBEと△ABDが相似であることを証明する問題。直角であることと、平行線の錯角から2組の角が等しいことを示す
B問題 1,2


1
(1)指数と正負の数の計算(2)文字式の分配法則の計算(3)文字式の乗除の計算
(4)文字式の計算(5)平方根の計算
2
(1)代入して式の値を求める問題(2)正の数と負の数の計算が常に正になるものを選ぶ問題
(3)二次方程式の問題。解の公式を使う(4)√44nが自然数となる最も小さいnを求める。44を素因数分解し、√( )²の形を作る


2
(5)積の値と和の値を場合分けし、bーaを計算する
(6)補助線CEをひき、∠AEC=90°であることを使う
(7)比例式を使う問題
(8)A(t,7/4t²)とおき、y=ー2x-1がC(t,ー7/4t²ー1)を通るので、代入してtを求める
B問題 3
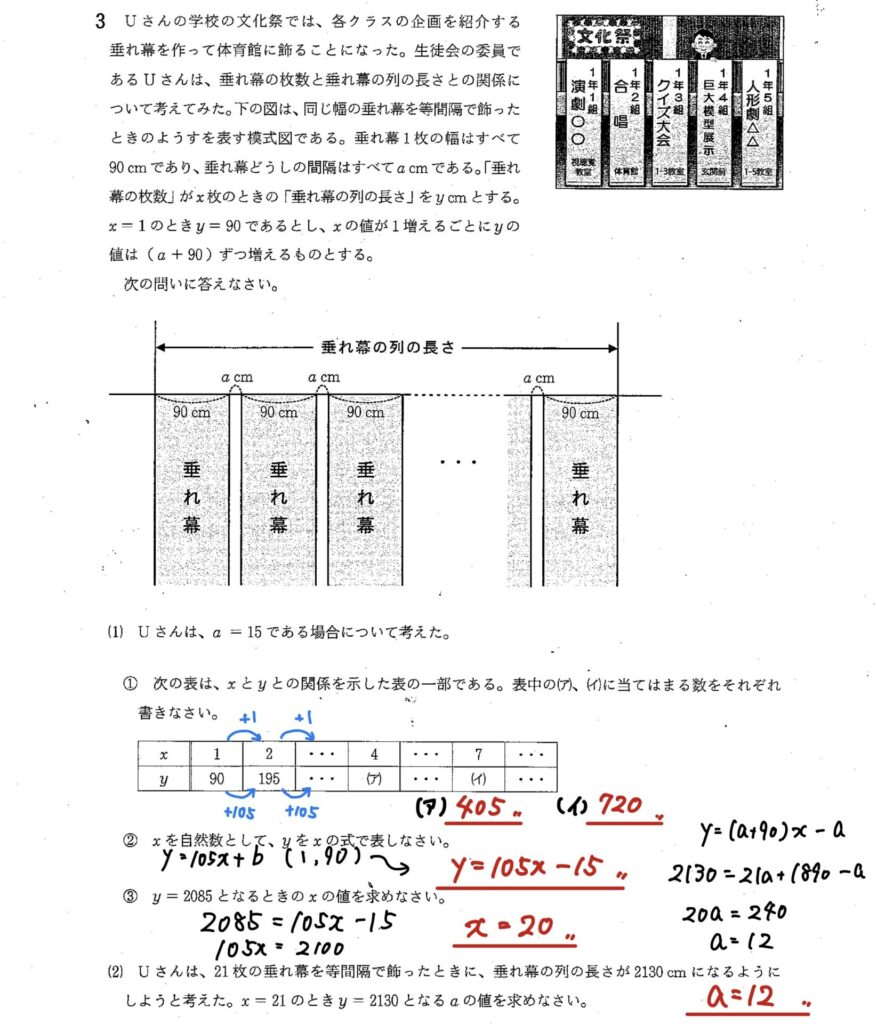
3
(1)
① 一次関数の表を完成させる問題
② y=105x+bが(1,90)のときの式を求める
③ yに2085を代入してxを求める
(2)y=2130,x=21になるようにaの値を求める
B問題 4
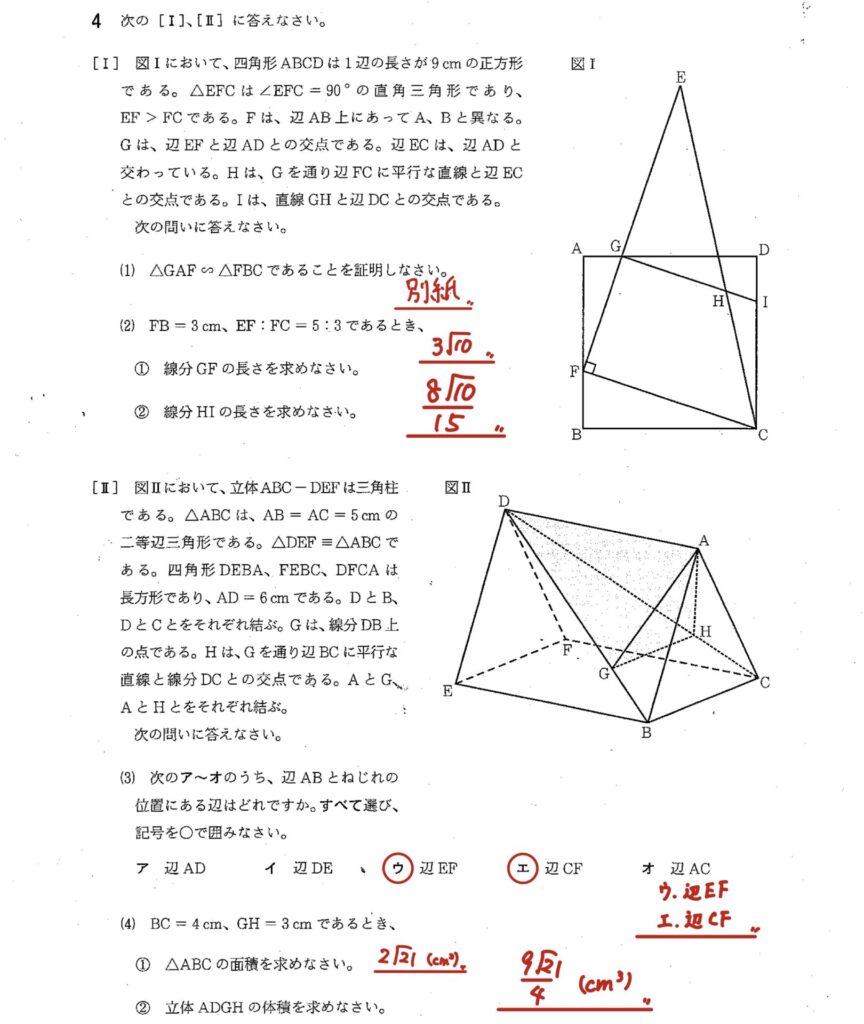
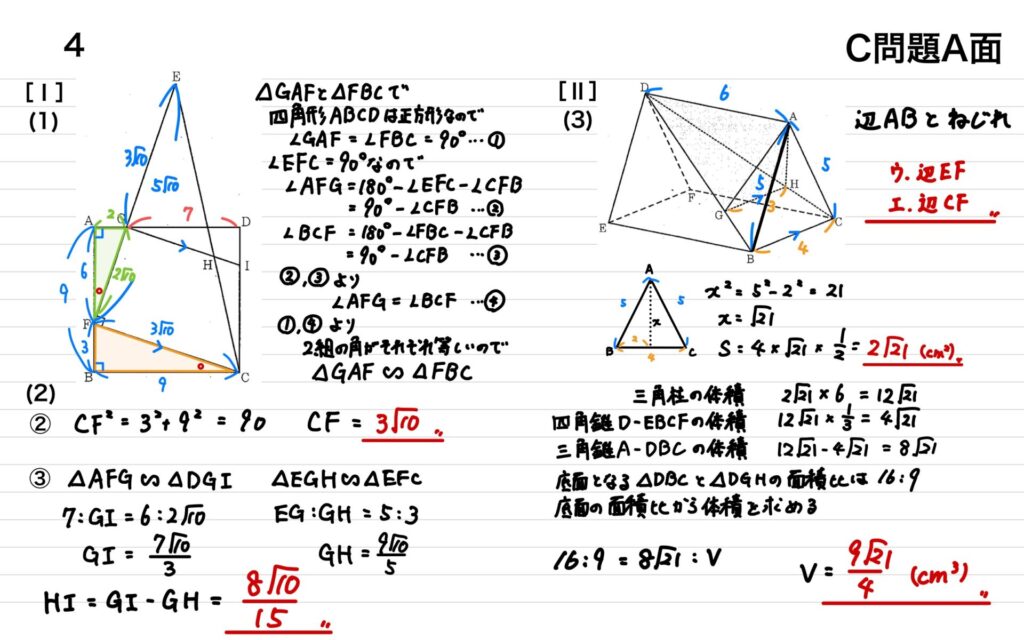
4
〔Ⅰ〕
(1)△GAFと△FBCが相似であることを証明する
(2)
② 相似比を使ってCFの長さを求める
③ 三角形の相似を使い、GIとGHの長さを求め、GHーGIからHIを求める
[Ⅱ]
(3)辺ABとねじれの位置にある辺を答える
(4)全体の体積から四角錐D-EBCFの体積をひいて三角錐A-DBCの体積を求め、底面となる△DBCと△DGHの面積比から体積を求める
C問題 1


1
(1)文字式の計算、通分して計算する
(2)平方根の計算、有理化と約分に注意が必要
(3)二次方程式の問題。x-7=Aとおき、因数分解してから解を求める
(4)代入すると、x=ー6のときy=ー9なので、x=aのとき最小値y=ー16をとることが分かる
(5)35x/12と21x/20が自然数になるためには、12と20の最小公倍数をかける必要がある。その後175と63はお互いに7を因数に持つので、7でわる


1
(6)それぞれ場合分けをして求める
(7)aとbをそれぞれn,m,lなどで表し、それぞれの条件にある組み合わせを探すと、(8,3)と(9,4)しかないことが分かる
(8)点A,Bをそれぞれaとbを使って表し、直線ℓの切片を求める式と四角形ABCDを求める式を連立方程式する
C問題 2

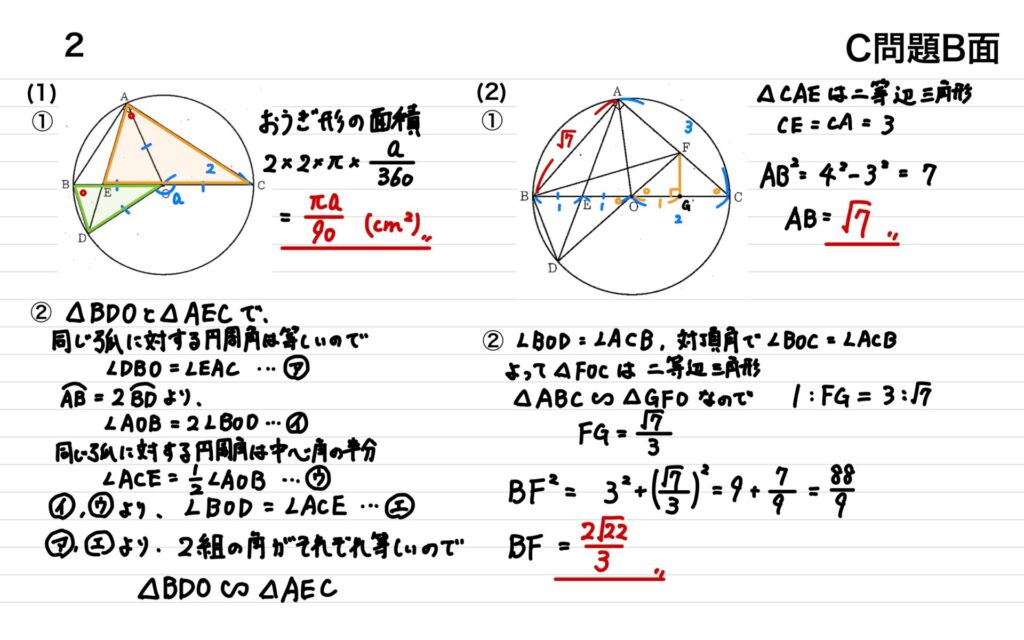
2
(1)
① 半径2㎝、中心核aのおうぎ形の面積を求める式をつくる
② 同じ弧に対する円周角と、弧の長さが1:2を使って、2組の角度が等しいことを示す
(2)
① △ABCで、辺ACは二等辺三角形という条件からAC=3と分かるので、三平方の定理を使ってABを求める
② △FOCが二等辺三角形、△OGF∽△ABCが分かるので、相似比から辺FGを求め、BGとFGから三平方の定理でBFを求める
C問題 3
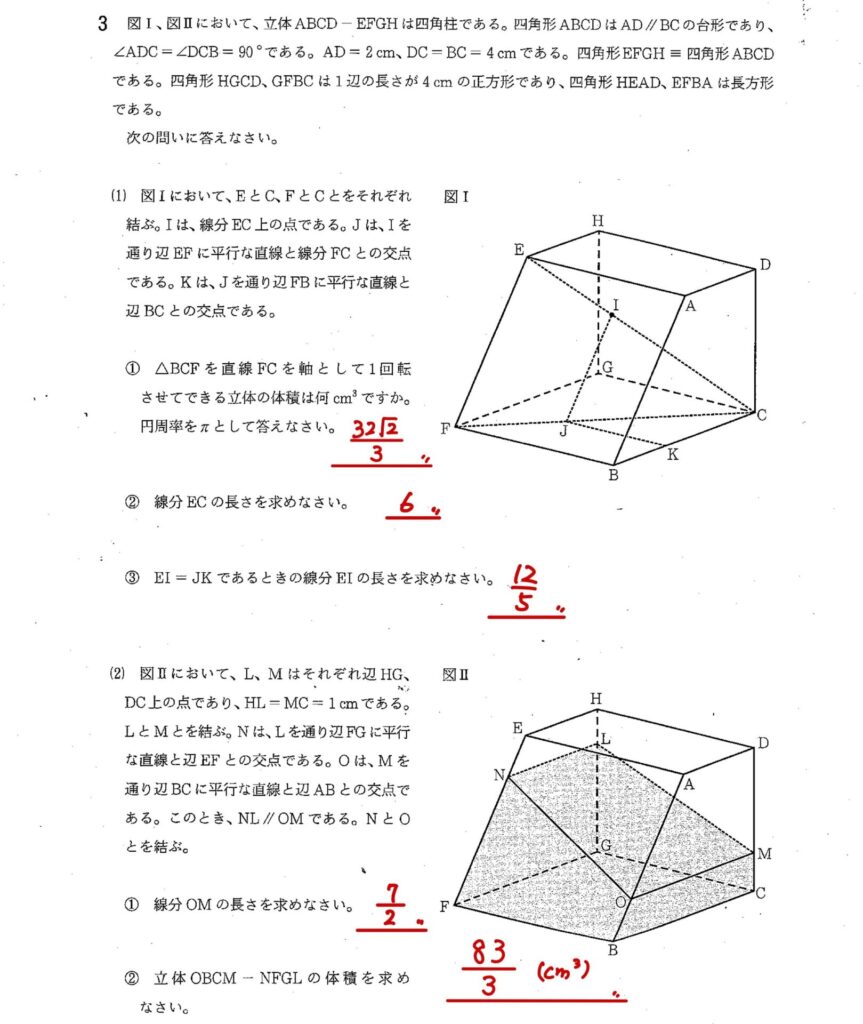
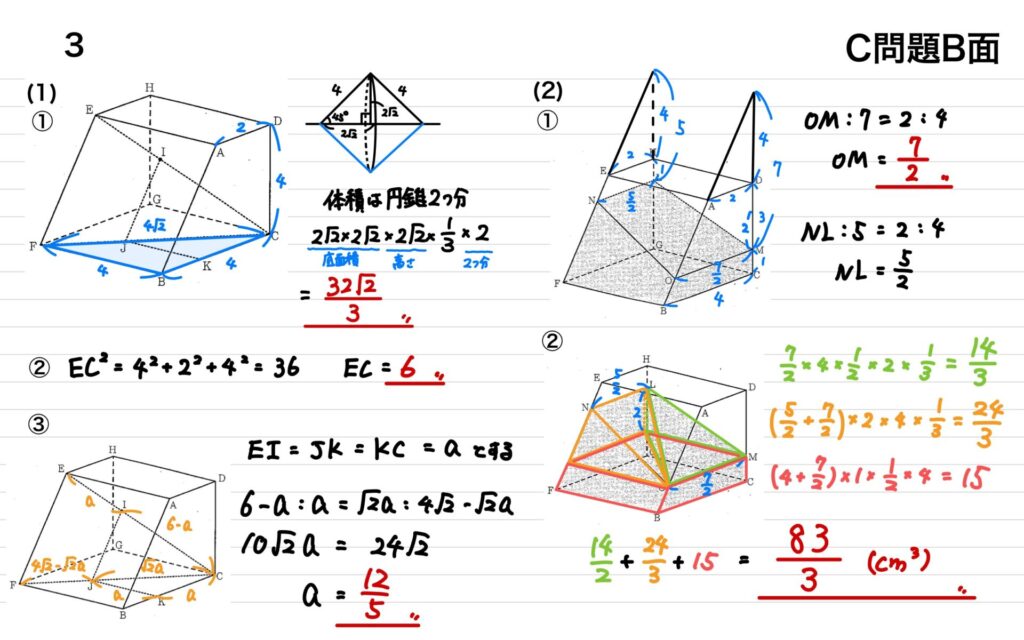
3
(1)
① 二等辺三角形BFCをFCを回転の軸として回転させると、円錐が二つくっついたような立体ができる
② 三平方の定理を使ってECの長さを求める
③ EI=JK=aとおくと、三平方の定理を使って、辺の長さをaを使って表すと図のようになるので、比を使ってaの長さを求める。
(2)
① 辺DCと辺ABを延長して三角形をつくり、比を使ってOMの長さを求める
② 図のように求める立体を三角錐、四角錐、台形柱の3つに分け、それぞれ体積を求める
投稿者プロフィール

-
現役で数学を教えている中学校の先生です。中学の数学のプリントやICT関連の情報、ブログでは道徳や学級レクのネタも発信しています。
このサイトはアフィリエイト広告(Amazonアソシエイト含む)を掲載しています。
最新の投稿
 ブログ2026年2月2日Keynoteの便利機能8選|知らないと損する使い方まとめ
ブログ2026年2月2日Keynoteの便利機能8選|知らないと損する使い方まとめ ブログ2026年1月30日【国民の祝日クイズ45問】意外と知らない日付とルールを4択問題でチェック!
ブログ2026年1月30日【国民の祝日クイズ45問】意外と知らない日付とルールを4択問題でチェック! ブログ2026年1月25日小・中学生の塾はいつから?教員が考える本当に意味のあるタイミング
ブログ2026年1月25日小・中学生の塾はいつから?教員が考える本当に意味のあるタイミング ブログ2026年1月24日教員が本音で答える|保護者からよく聞かれる勉強の悩み8選
ブログ2026年1月24日教員が本音で答える|保護者からよく聞かれる勉強の悩み8選





