【算数の素朴な疑問を解決】子供に聞かれたらあなたは答えられる？

算数の授業を受けていて、「なんでだろう？」と思うことありませんか？

「マイナス×マイナスはなぜプラスになるのか？」「分数の割り算はなぜ逆数するのか？」当たり前のようにやっていても、なぜか？と問われると、答えられる人は多くはないでしょう！

そこで今回の記事は、算数の素朴な疑問と、その回答をご紹介したいと思います。

RISU算数（タブレット学習教材）を現役数学教師がレビューしました！

↓↓↓Instagramもフォローしてね！

Instagramを見る

　マイナス×マイナスはなぜプラス？

　お金で考えよう！

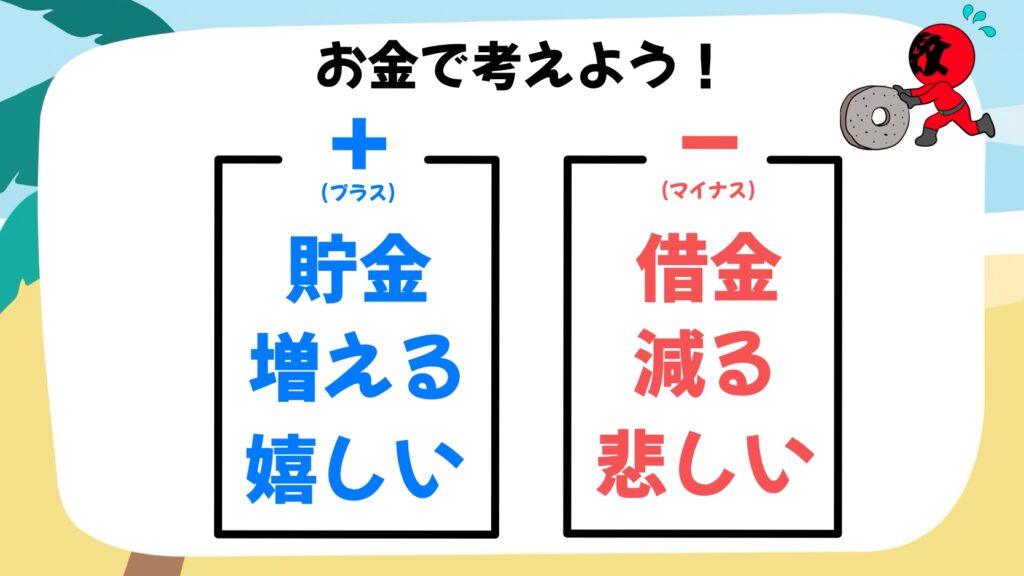
プラスとマイナスをお金で考えてみましょう。

プラスをそれぞれ「貯金」「増える」「嬉しい」とします。マイナスをそれぞれ「借金」「減る「悲しい」とします。

このプラスとマイナスの言葉をそれぞれ組み合わせて考えることで、「マイナス×マイナス＝プラス」を理解することができます。

　プラス×プラス＝プラス

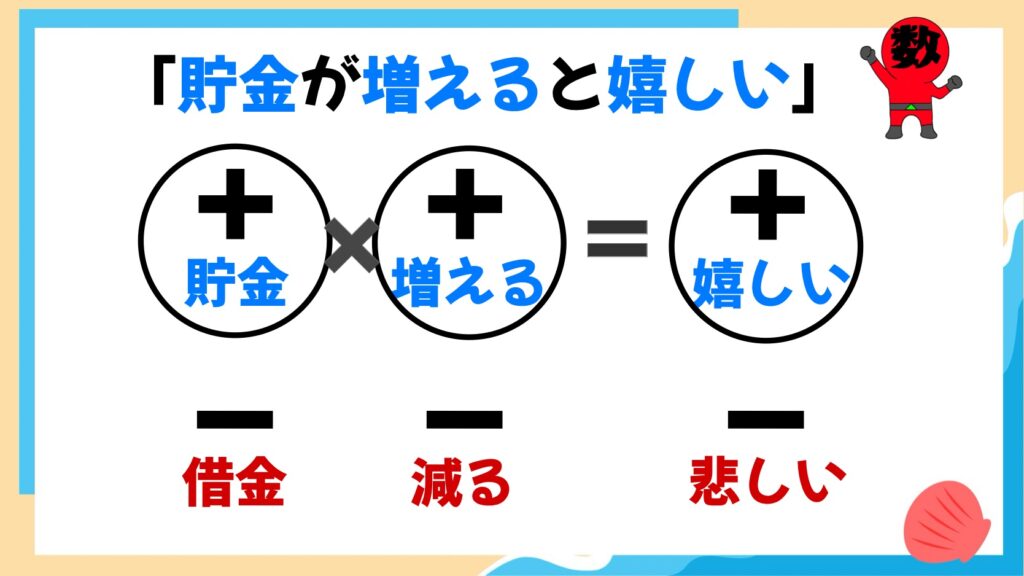
まずは「プラス×プラス＝プラス」です。これは当たり前ですが、一応説明しておきます。

「貯金」が「増えたら」「嬉しい」ですよね？単純にプラスの意味のものが二つ重なるとプラスの気持ちになりますよね。

　プラス×マイナス＝マイナス

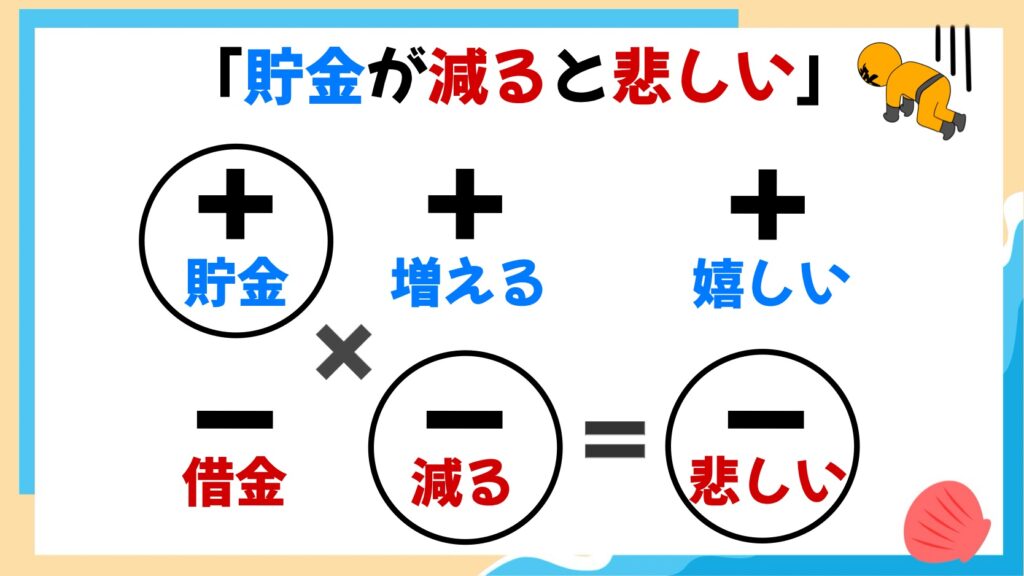
次に「プラス×マイナス＝マイナス」ですが、「貯金」が「減る」ことは「悲しい」ですよね？

プラスのものが減少することは、マイナスの気持ちになりますね。

　マイナス×プラス＝マイナス

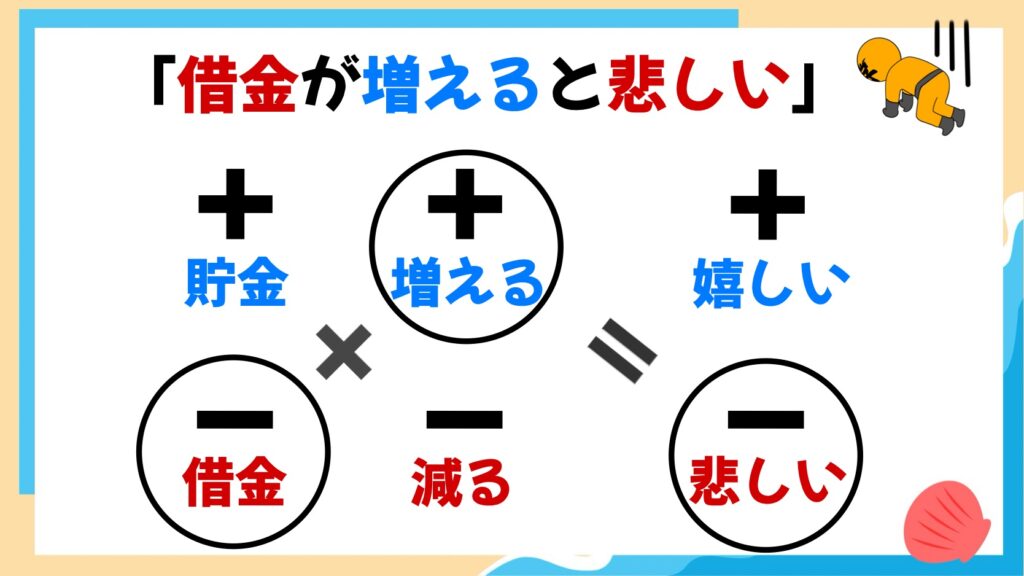
次は「マイナス×プラス＝マイナス」です。「借金」が「増える」のは「悲しい」ことです。

マイナスのものが増えるとマイナスの気持ちになりますね。

　マイナス×マイナス＝プラス

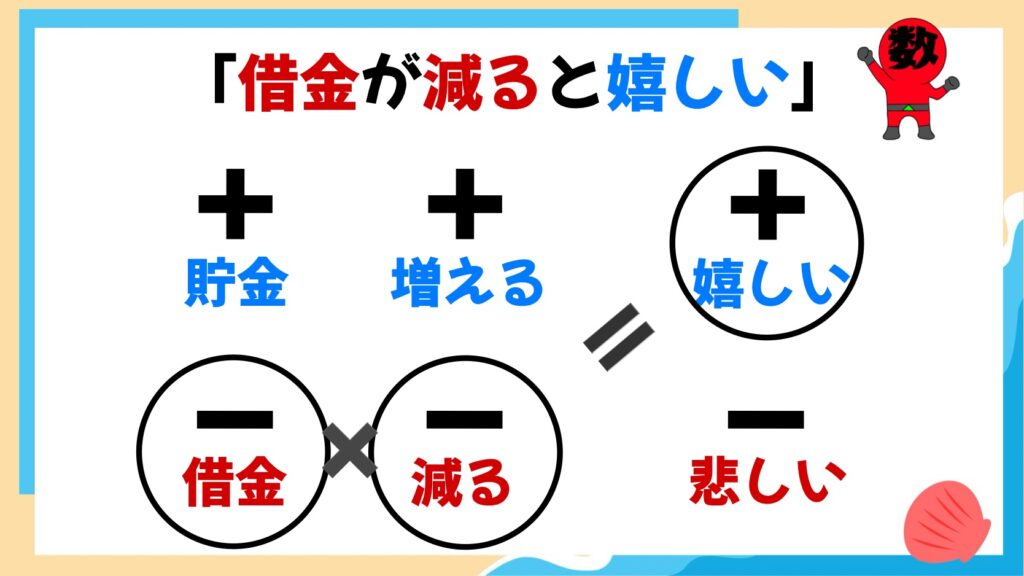
ここまでのことが納得がいけば、「マイナス×マイナス＝プラス」も簡単に説明がつくでしょう。「借金」が「減る」ことは「嬉しい」ことです。

マイナスのものが減ることは良いことですよね。これが「マイナス×マイナス＝プラス」になる理由です。この説明であれば、子供も納得して前に進むことができるでしょう。

　こんな説明も

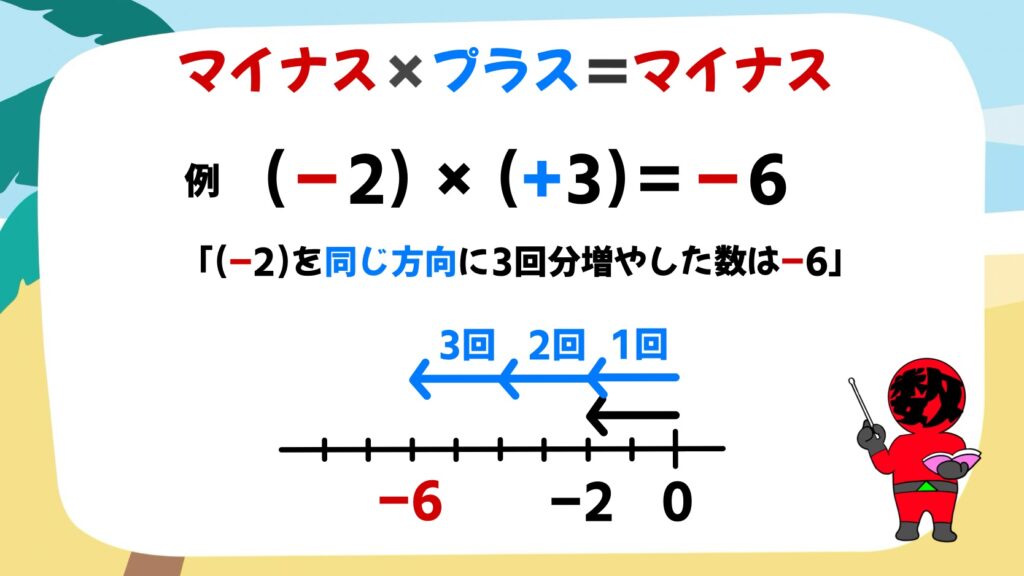
「マイナス」×「プラス」＝「マイナス」

例えば（ー２）×（＋３）＝ー６は、（ー２）を同じ方向に３回増やした数を表すので、「ー６」になります。

「プラス」×「マイナス」＝「マイナス」

　（＋２）×（ー３）＝ー６は、（＋２）を逆方向に３回増やした数を表すので、「ー６」になります。

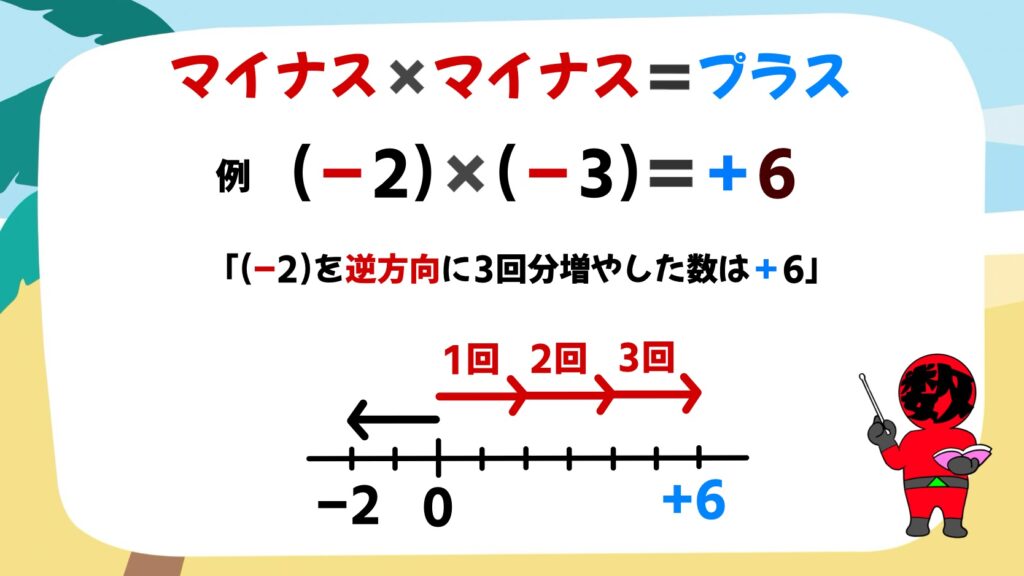
「マイナス」×「マイナス」＝「プラス」

　（ー２）×（ー３）＝＋６は、（ー２）を逆方向に３回増やした数を表すので、「＋６」となります。

　かけ算やわり算を先に計算するのはなぜ？

　答えが複数出てしまうから

結論から言うと、かけ算やわり算を先に計算する理由は、「ルールがないと答えが複数出てきてしまうから」です。

かけ算やわり算から計算しなければいけないという数学的な決まりはないみたいですが、ある一定の決まりがなければ、答えが２つ出てきてしまうような問題が存在します。

つまり、かけ算やわり算を先に計算すると決めておかないと答えの食い違いが生じてしまうからです。

　１０－４×２を考える

ここで１０－４×２という問題を考えてみましょう。

もし左から順番に計算した場合、１０－４＝６を先に計算し、６×２＝１２という答えになりますね。

一方でかけ算を先に計算した場合は、４×２＝８を先に計算し、１０－８＝２という答えになります。

同じ計算でも答えが二つ出てきてしまいましたね。解く人によって答えが違ってしまったら困りますよね。

ではなぜ、たし算やひき算ではなく、かけ算とわり算を先に計算することになったのか、下の単位の違いで説明してみましょう。

　単位の違いで考える

例えば、「１００円のお菓子３つと１２０円のジュースを買った代金の合計は？」という問題があったとします。

式にすると”１００×３＋１２０”となり、小学校３年生くらいで習う計算式になります。

単位を付けてみると”１００円×３個＋１２０円”

この計算式を”３個＋１２０円”を先に計算するのは式の意味合いからするとおかしいことが分かりますね。

「１００円お菓子を３個買った代金」と「１２０円のジュースの代金」の合計を求めなくてはいけないので、かけ算から先に計算することになります。

　わり算とかけ算の計算は左から

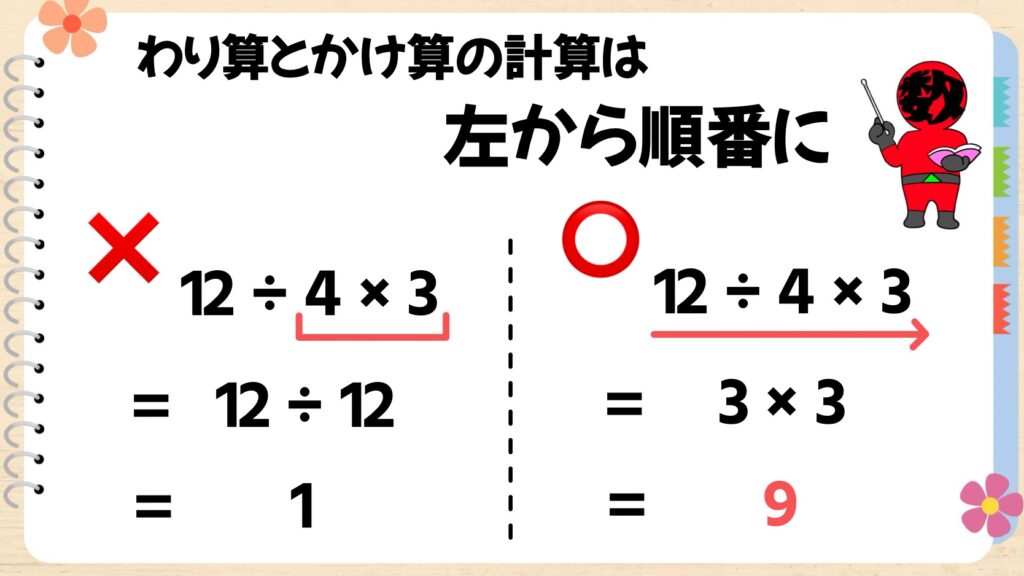
「かけ算とわり算の式では左から順番に計算する」という決まりがあります。これも、答えが複数出てきてしまうからという理由です。

「１２個のケーキを４人で分けることを３回繰り返したら、１人何個ケーキを食べられる？」という問題考をえてみると、１２個のケーキを４人で分ける時点で１人３個は食べられるはずなのに、答えが１になるのはどう考えてもおかしいですよね。

４×３を先に計算してしまうと、１２個のケーキを１２人で分けることになっていまい、問題の意味とは大きく変わってしまいます。　

他にもこんなことができる

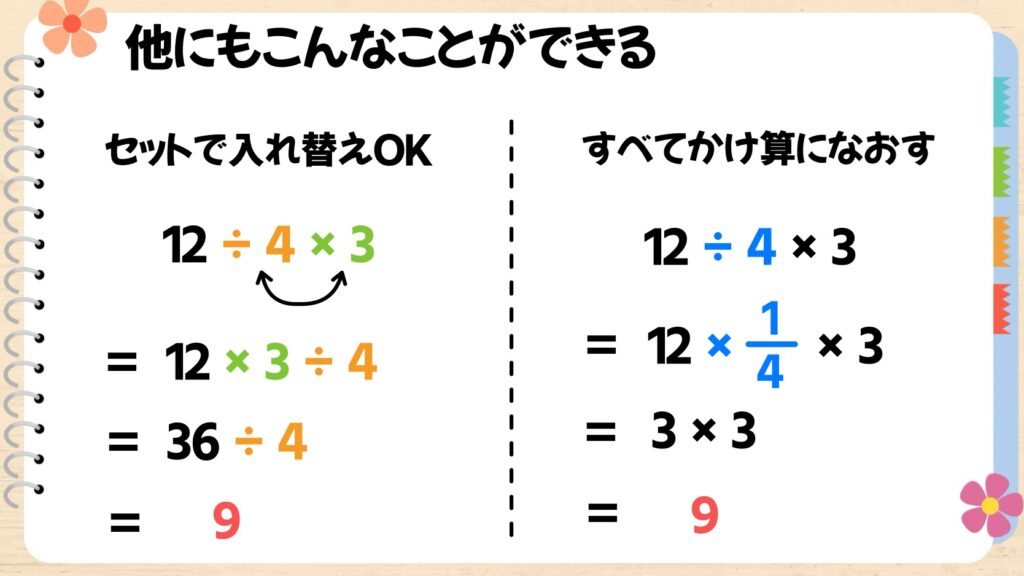
「÷４」と「×３」の計算記号をセットで入れ替えることができます。

先ほどの問題で考えると、「１２個入りのケーキ３箱を、４人で分けたら１人何個ケーキを食べられる？」という意味となり、答えは３６÷４＝９となります。

また、わり算をかけ算に直してから計算する方法もあります。

　中学生への繋がり

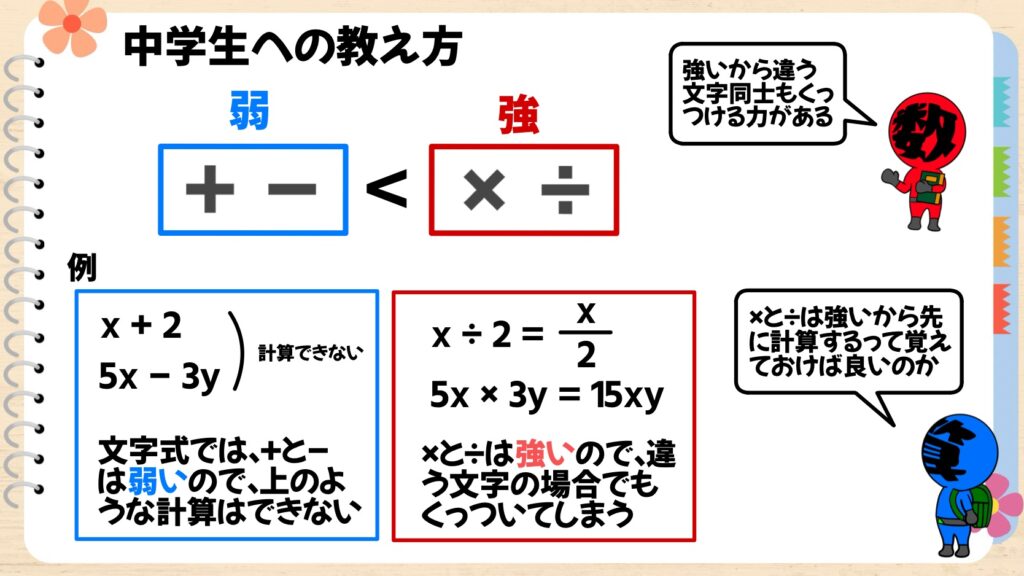
僕は中学生には「たし算ひき算とかけ算わり算には強弱がある」ということを教えています。（あくまでイメージの世界ですが）

中学１年生の数学では文字の式という単元で、小学校ではやらなかった、かけ算の省略や文字を使ったわり算が登場します。

例えば”ｘ＋２”や”５ｘー３ｙ”などの、文字が違う場合のたし算やひき算は計算ができません。なぜならば、「＋と－はくっつける力が弱い」からです。

一方”ｘ÷２”や５ｘ×３ｙ”は、それぞれｘ/２、１５ｘｙとわり算は上下に、かけ算は前後にくっついてしまいます。「×と÷はくっつける力が強い」からです。

このように、＋と－、×と÷には明確に強さが違う。だから同じ式に＋と×がある場合は強い×から先に計算するということです。

　議論を巻き起こした6÷2(1+2)

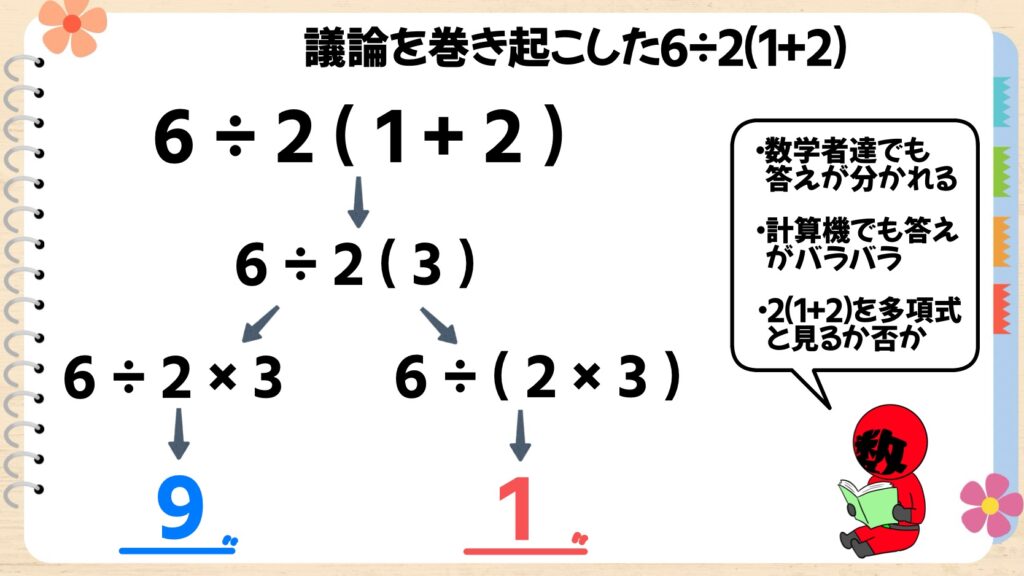
上の画像の問題は、SNS上で話題になった有名な問題です。

計算の順番としては、（　）→×÷→＋－という順番になるので、まずは（１＋２）＝３から計算します。ここまでは誰でも分かります。

問題はそのあと、この計算を”６÷２×３”と考えるのか、６÷（２×３）と考えるのかで、数学者達の間でも答えが分かれてしまいました。また、電卓で計算しても、メーカーによって答えが２通り出てくるというのだから驚きですよね。

２（１＋２）を１つの塊（多項式）としてみるかどうかで答えが変わってしまうということです。

この式の問題点は、通常普通の計算では省略しない×を省略してしまったことから、このような話題になるに至ったそうです。

　三角錐や円錐の体積の求め方は？

　水を使った解説

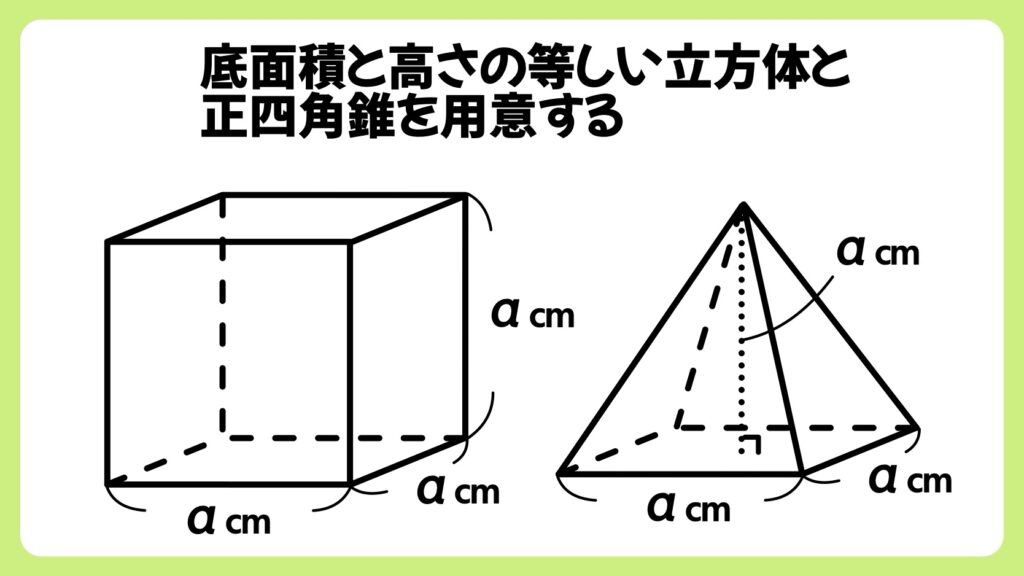
まずは上の画像のような、同じ底面積、同じ高さの立方体と正四角錐を用意します。

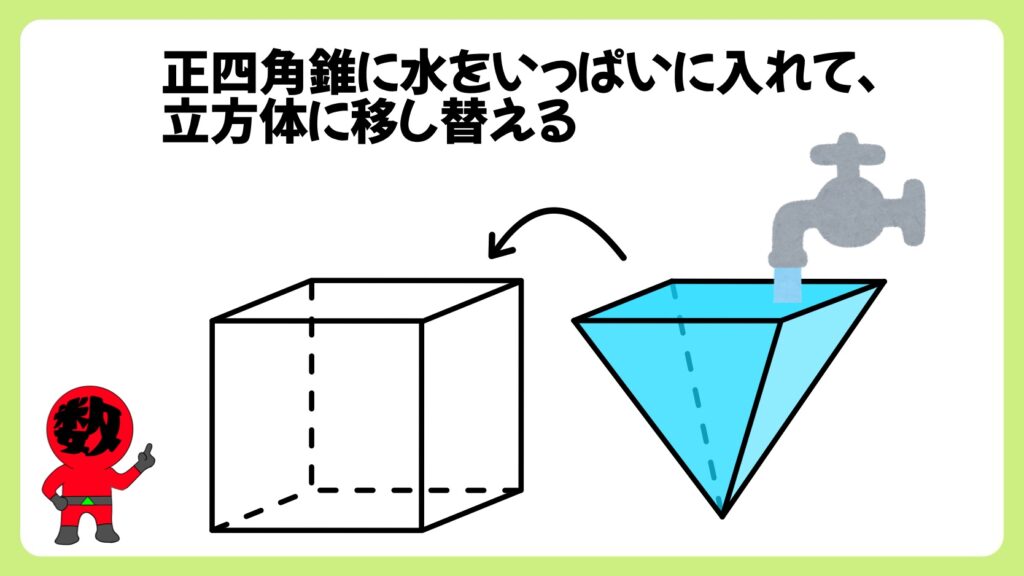
この正四角錐に水を一杯に入れ、正四角錐に水を移し替えていきます。

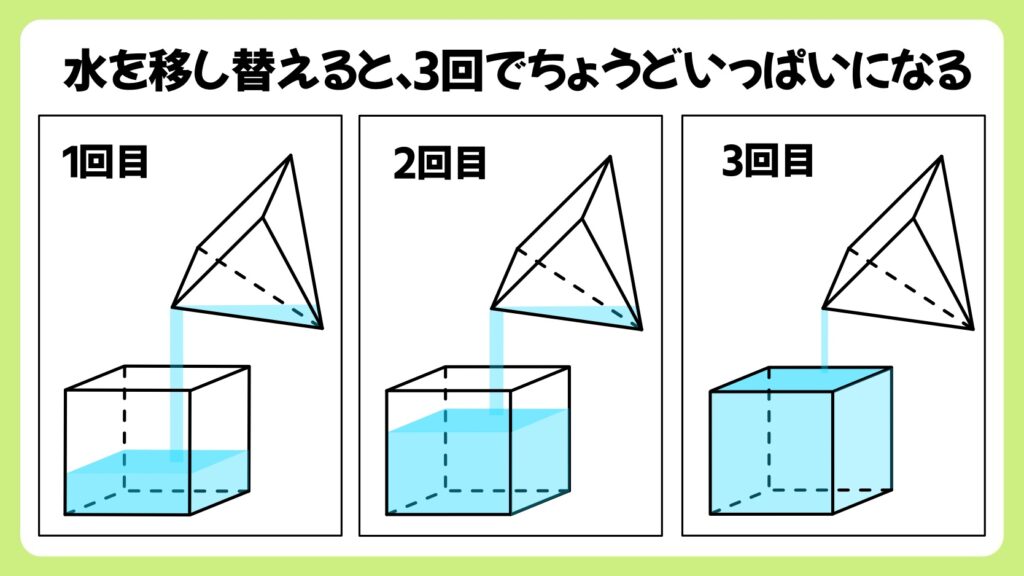
実際に模型を使って、子供の前でやってみたことがあるのですが、「何杯でいっぱいになると思う？」と質問すると、多くの子供が「２杯！」と答えます。確かに見た目の大きさからすると２杯くらい見えるんですよね。

実際には３杯で正四角錐はちょうどいっぱいになります。

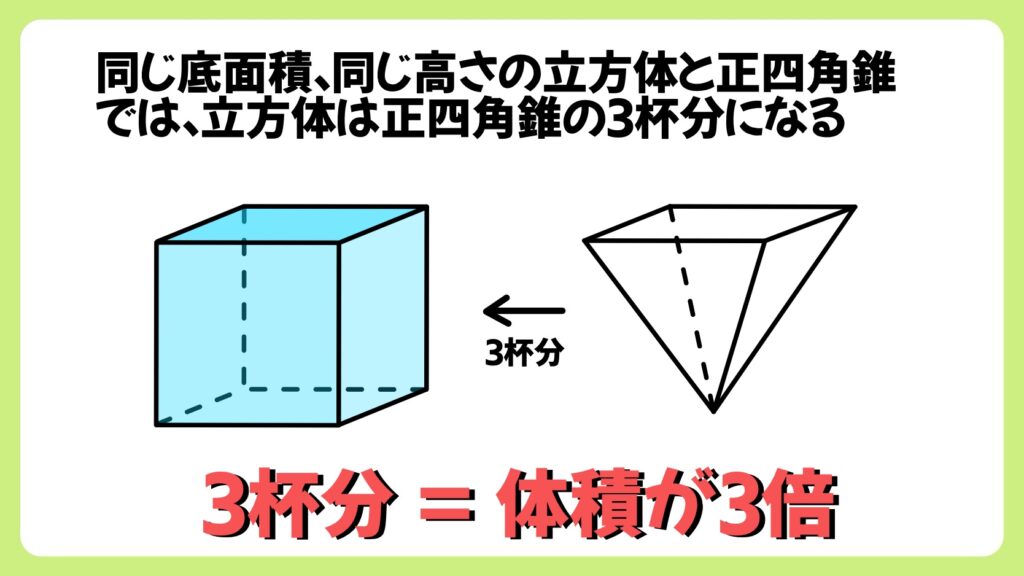
つまり、同じ底面積、同じ高さの立方体と正四角錐では、立方体は正四角錐の３杯分になるということが分かるので、体積が３倍であることが分かります。

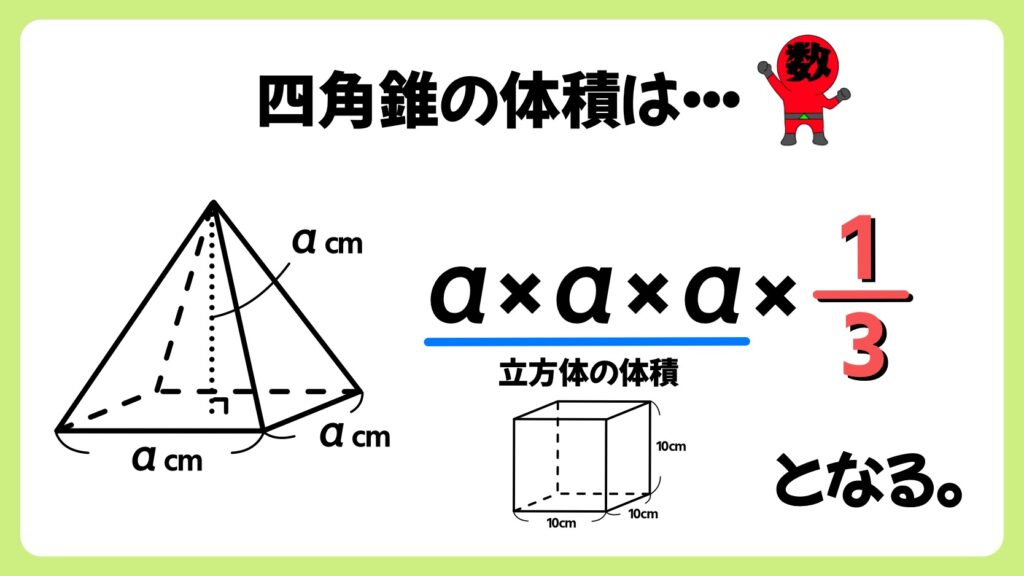
よって、この正四角錐の体積は、同じ底面積、同じ高さを持つ立方体の体積の１/３となります。

　V＝１/３Sa であることの証明

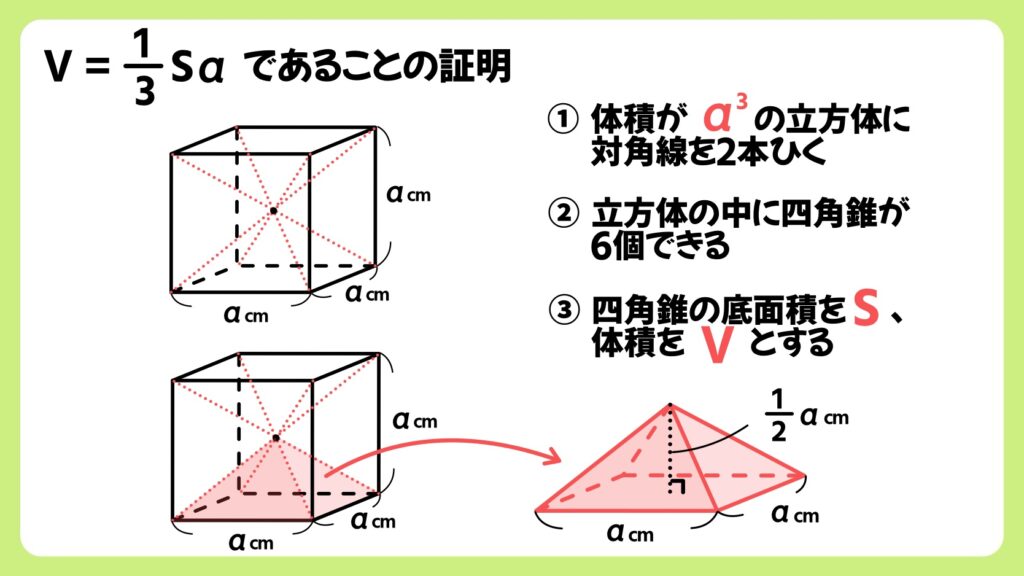
１辺がacmの立方体に対角線を２本ひくと、立方体の内部に正四角錐が６個作ることができます。この正四角錐は、底面の正方形の１辺がacmで、高さが１/２acmの正四角錐となります。

この正四角錐の底面積をS、体積をVとすると、

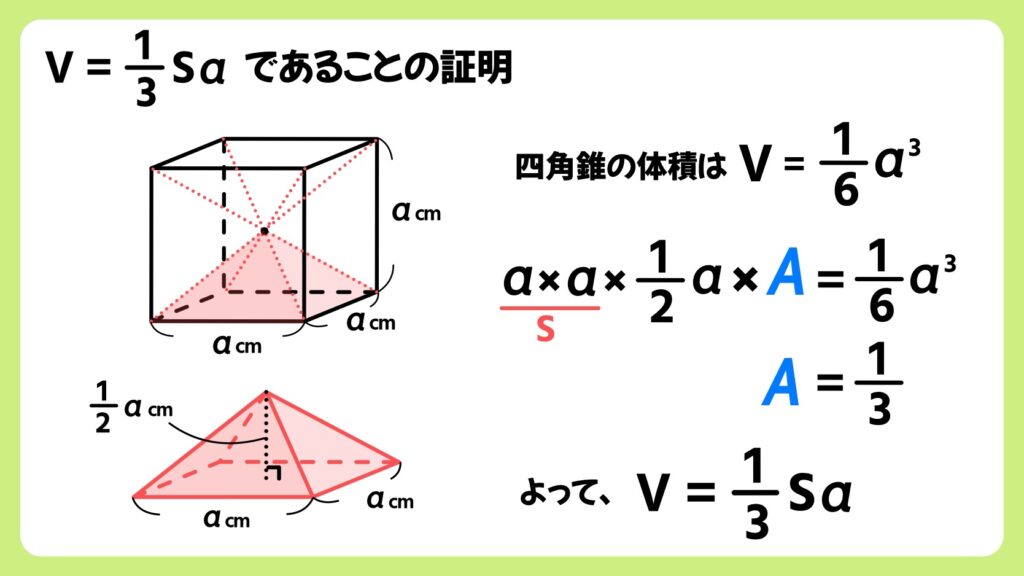
正四角錐の体積は１/６a^3となり、V＝１/３Saであることが分かります。

　多角形の内角の和はなぜ180(n-2)？

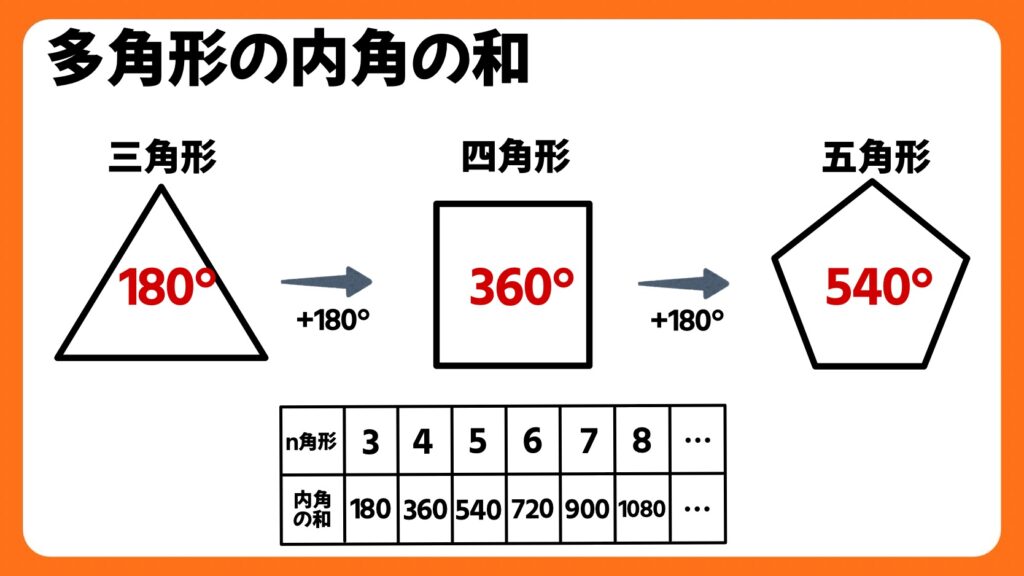
まず多角形とは角が３つ以上ある平面図形のことを、多角形といいます。そして多角形の内側の角のことを内角といいます。

三角形は、それぞれの角を組み合わせると180°、もしくは平行線の錯角と同位角を使うことで180°であることが証明できます。

また、四角形や五角形の内角の和は、上の画像のように、角が１つ増えるごとに180°ずつ増えていきます。そう、内角の和には規則性があるのです。

　規則性のある内角の和を式に表すと、（角の数－２）×180で求められることが分かります。これをｎを使って表したものが180°×（n－2）という式なのです。

　なぜ180° ×（ｎー2）で求められるのか？

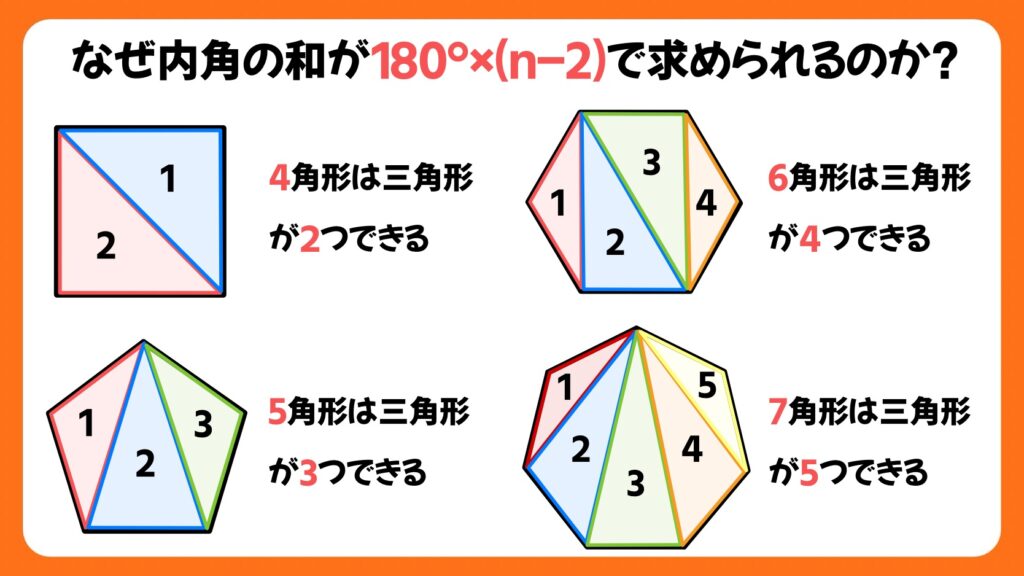
ｎ角形の内角の和がなぜ180° ×（ｎー2）という式で求められるかというと、ｎ角形の中には（ｎー２）個の三角形を作ることができるからです。

上の画像のように、４角形は三角形が２つ、５角形は三角形が３つでき、６角形は三角形が４つでき、７角形は三角形が５つできることが分かります。

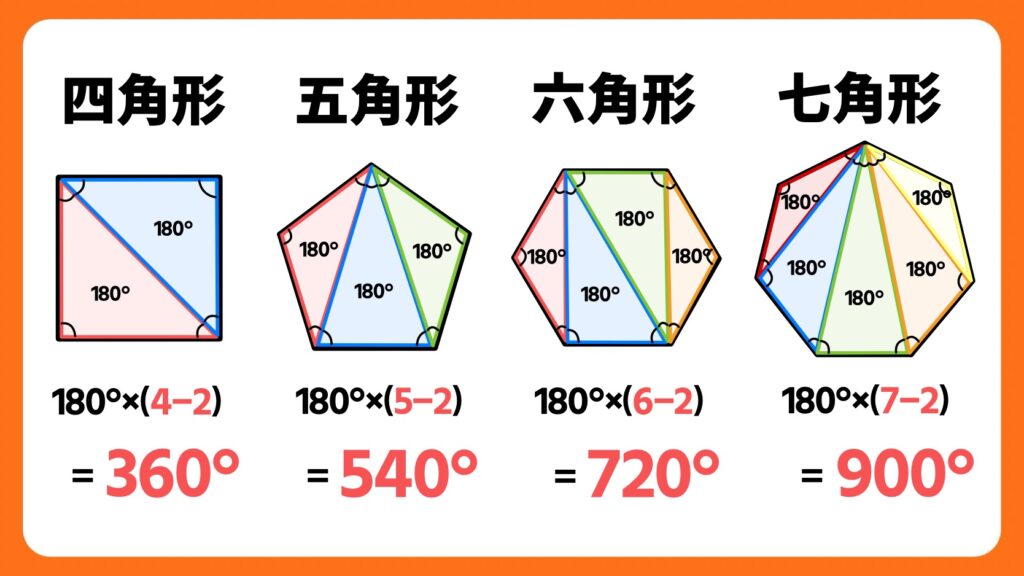
　三角形の内角の和は180°なので、できる三角形の数×180°ということになります。多角形の角が１つ増えることによって、できる三角形は１つずつ増えていきます。

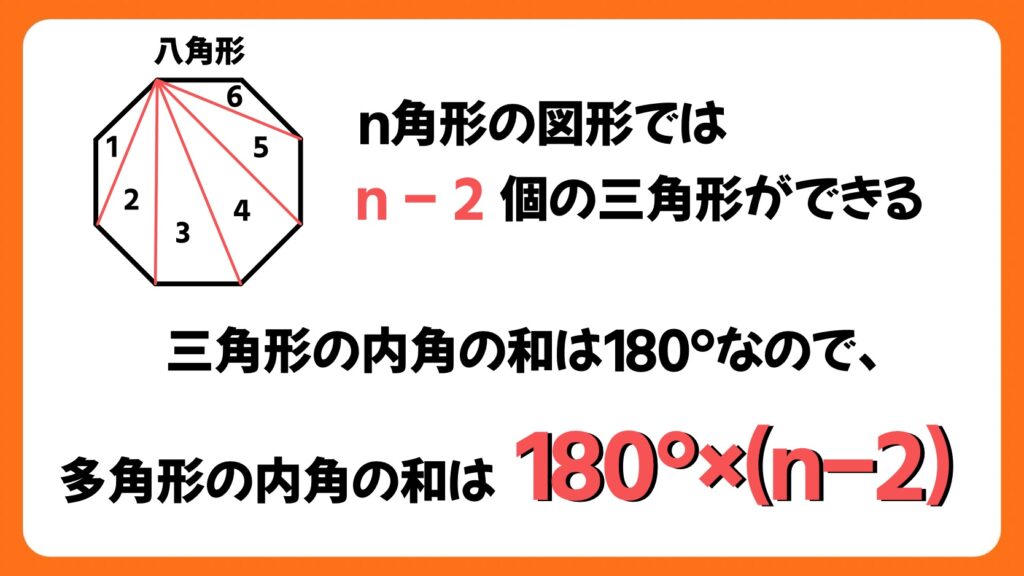
つまり、（ｎー２）個の三角形が作れるｎ角形の内角の和は、180° ×（ｎー2）という式になるということです。

　もう一つの考え方

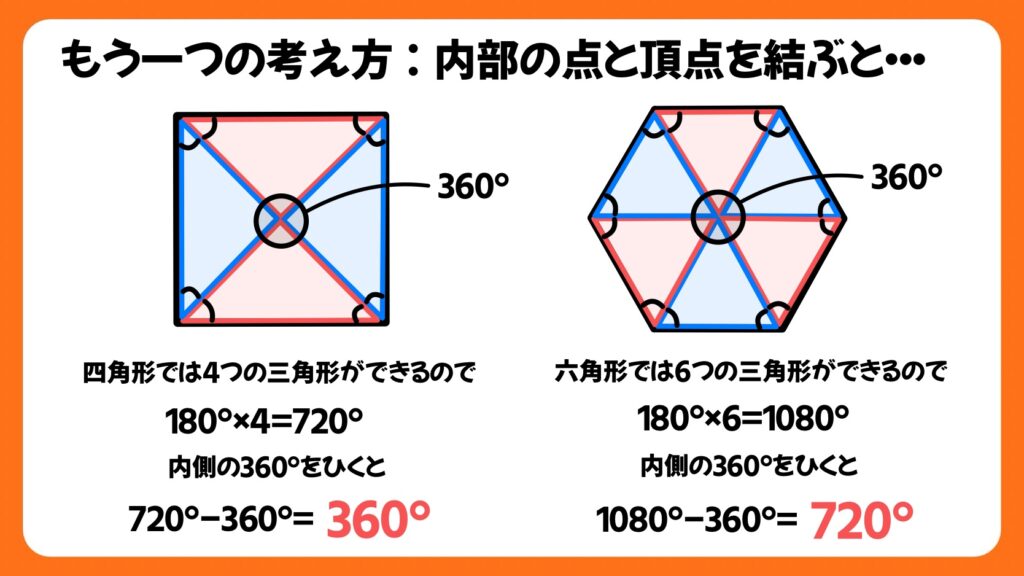
もう一つの考え方を紹介します。まずは多角形の頂点から対角線をひきます。

画像の左のように、四角形では三角形が４つでき、全ての角を合わせると、180°×４＝720°となります。また、画像の右側は六角形の中に三角形が６つでき、その角の合計は180°×６＝1080°となります。

中央の円（360°）は内角の和には関係のない角なので、それぞれの合計の角から360°をひくと、内角の和を求めることができます。

　三角形の内角の和はなぜ180°？

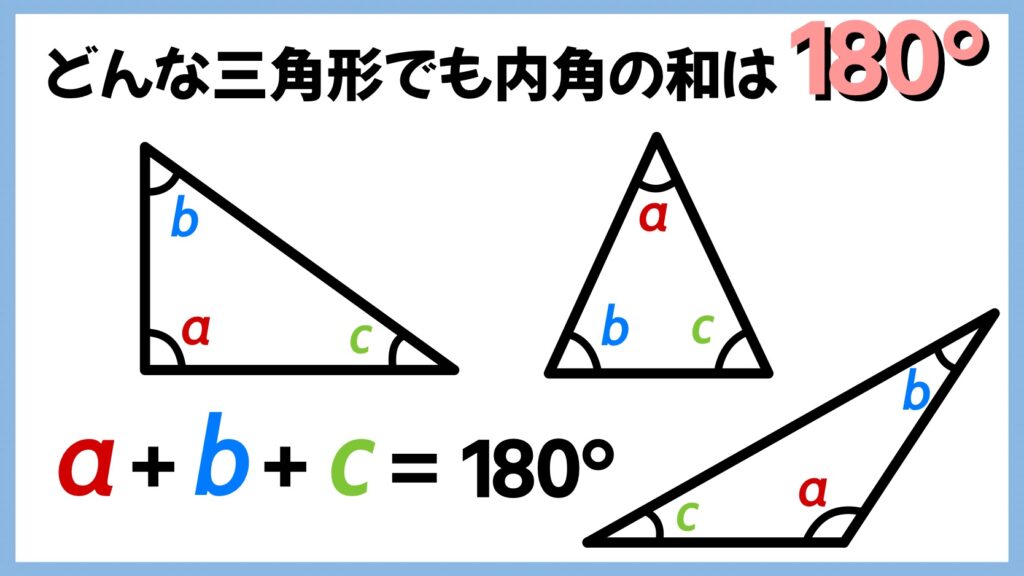
三角形にはいろんな種類があります。直角三角形、二等辺三角形、鋭角三角形や鈍角三角形。形や大きさは様々ですが、どんな三角形でも、「3つの角の内角をすべて足すと絶対に180°になる」という性質があります。

　なぜ180°になるのか？

　３つの同じ三角形を組み合わせる

下の画像のように、合同の三角形を3つ用意し、１つをひっくり返します。

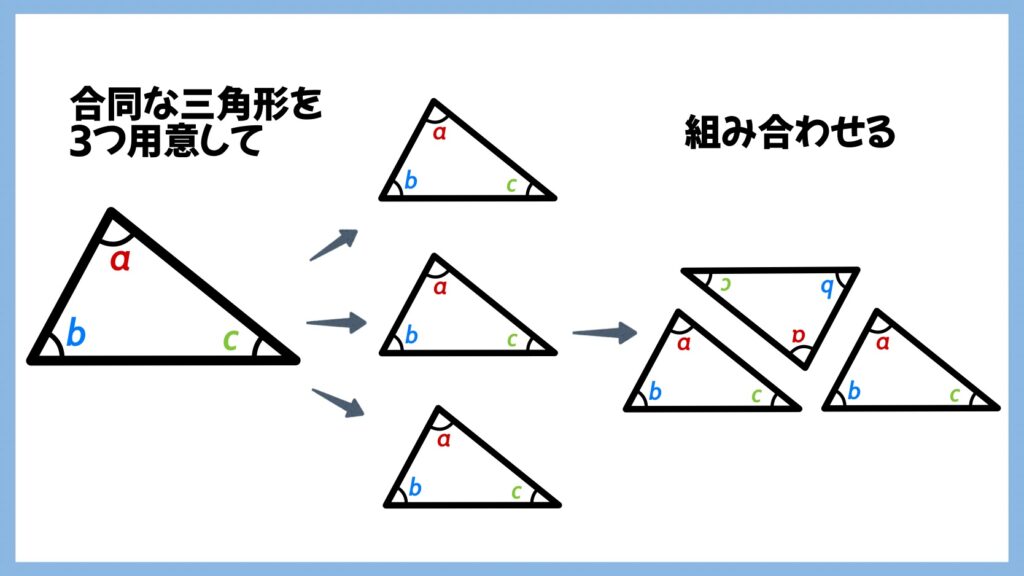
　それぞれの角を足すように並べると、一直線（180°）になることが分かります

　三角形の角を切って組み合わせる

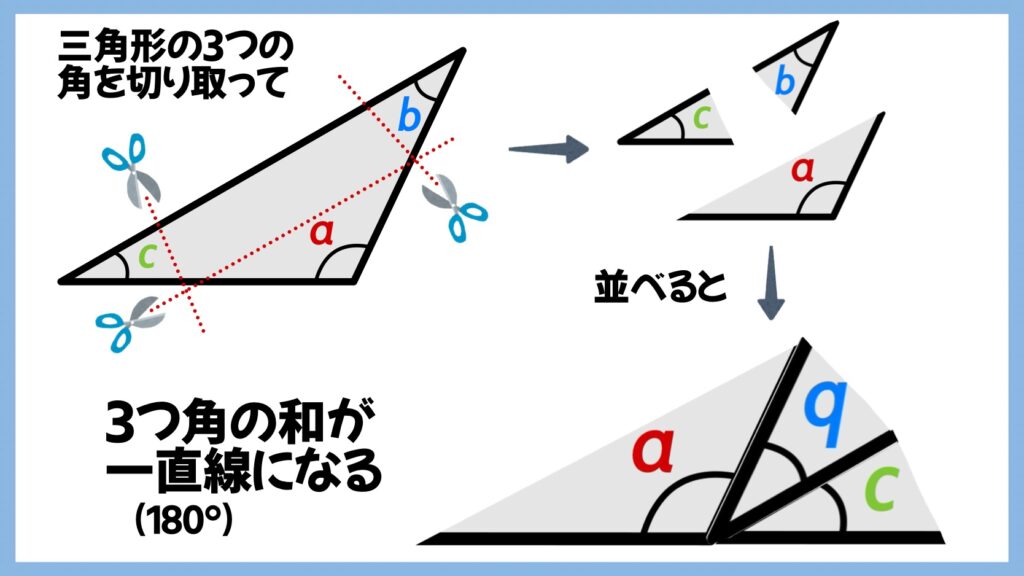
１つの三角形の角を切り取って、画像の右下のようにつなぎ合わせると、３つの角の和が一直線（180°）になることが分かります。

　中学生向けの証明

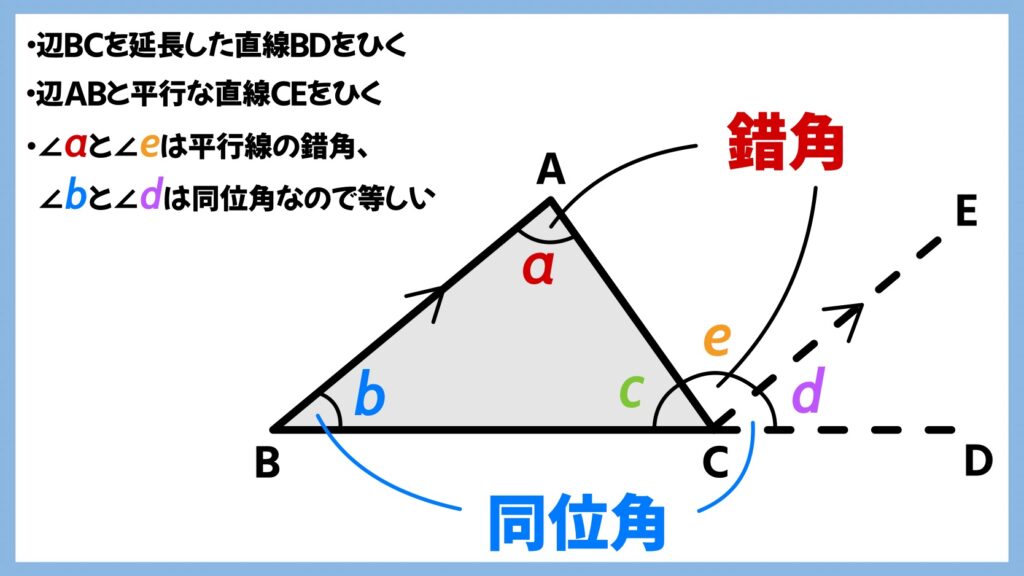
上の画像のような△ABCで、辺BCを延長した直線BDをひきます。次に辺ABに平行な直線CEをひきます。

∠a=∠eは平行線の錯角、∠ｂと∠ｄは平行線の同位角なので等しくなります。よって、∠ｃ＋∠e＋∠d＝180°となります。

　おうぎ形の面積や中心角はどう求める？

　扇形とは

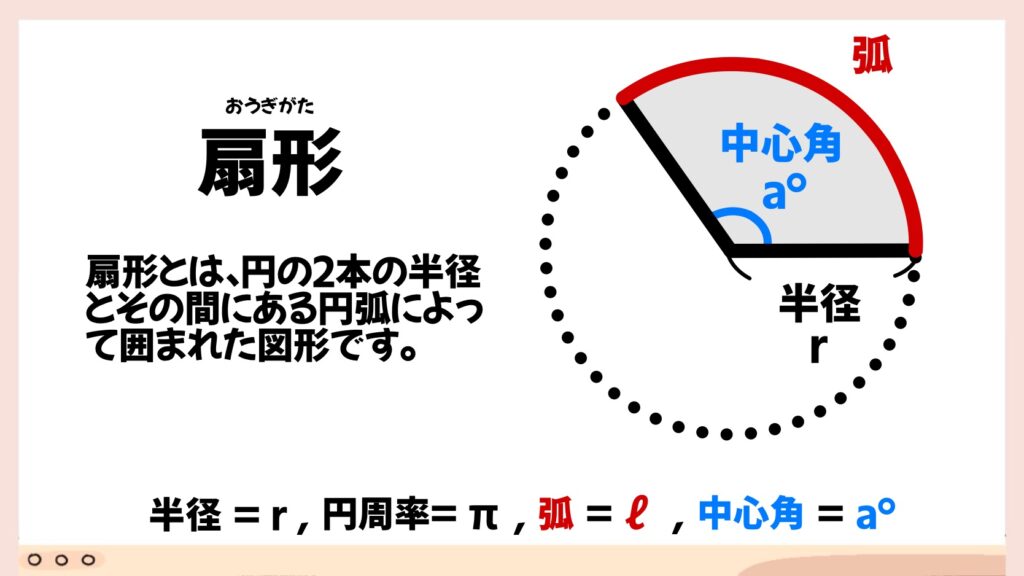
まずは扇形（おうぎがた）について、基本的なことを確認しておきましょう。

扇形とは、円の２本の半径と、その間にある円弧（半径同士を繋いでいる曲線部分）によって囲まれた図形のことをいいます。ピザの欠片のように、円の一部を切り取った図形と考えましょう。

S は扇形の面積、π は円周率、r は円の半径、a は中心角、ℓは弧の長さを表します。

　面積の求め方

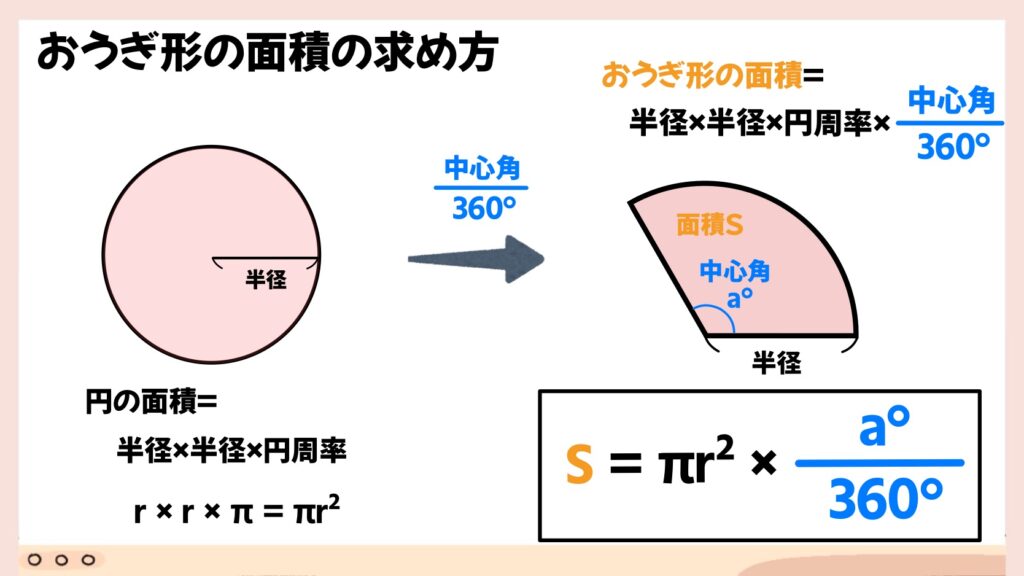
扇形の面積を求めるときは、もとの円と比べてどれくらいの大きさなのか、を考えます。扇形と同じ半径をもつ円の面積に、中心角の割合をかければ求められます。

扇形の中心角の1° というのは、円の中心角 360° の360分の1の大きさです。例えば、中心角 40° の扇形の面積は、半径が等しい円の面積の360分の40、つまり、9分の1の大きさになります。

　半径と弧の長さから面積を求める

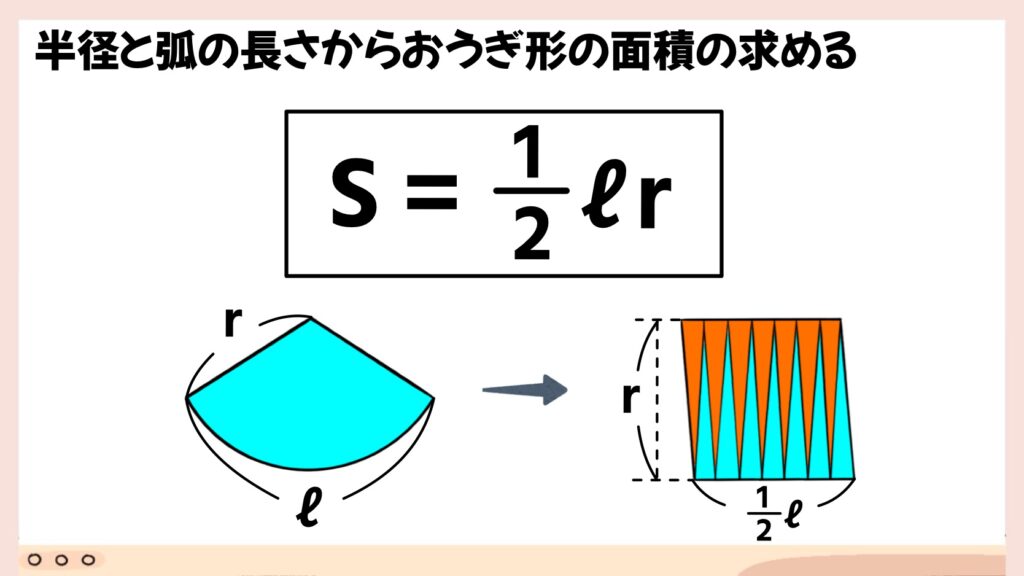
扇形にはもう一つ、面積の求め方があります。

図のように、扇形を限りなく細かく切っていき、それを互い違いに並べると平行四辺形が出来上がります。縦の長さは半径ｒとなり、横の長さは弧の長さの半分になるので、１/２ℓとなります。

よって、面積S＝１/２ℓｒという式が成り立ちます。　扇形の面積公式を覚えたら、ついでに弧の長さ公式も一緒に覚えてしまいましょう。覚えておくと大変便利です！

　弧の長さの求め方

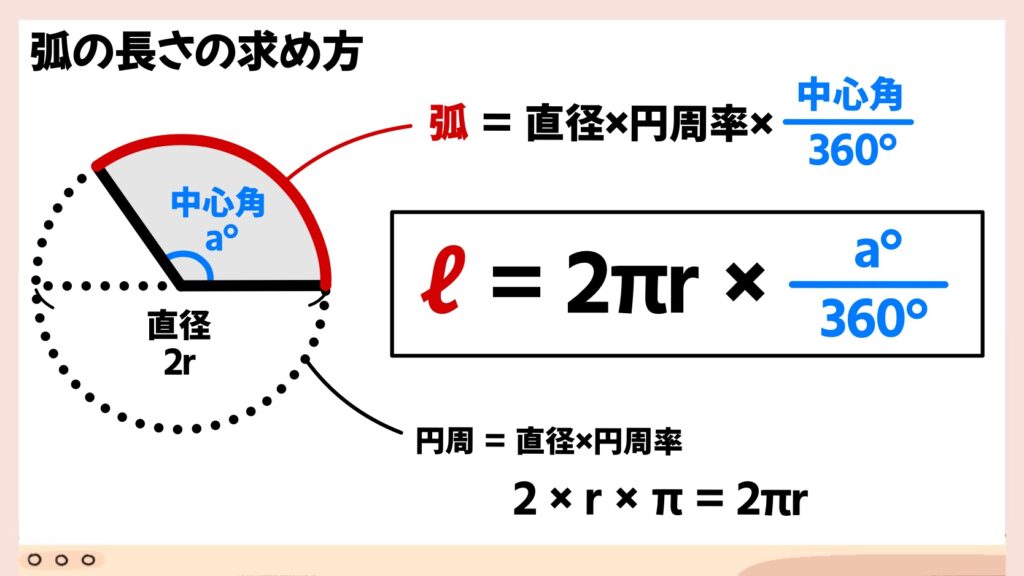
扇形の弧の長さは、面積を求めるときと同じ考え方で求めることができます。もとの円の円周と比べてどれくらいの長さなのか、を考えましょう。扇形と同じ半径をもつ円の円周の長さに、中心角の割合をかければ求められます。

例えば、中心角 120° の扇形の弧の長さは、半径が等しい円の面積の360分の120、つまり、3分の1の大きさになります。

　弧の長さから中心角を求める

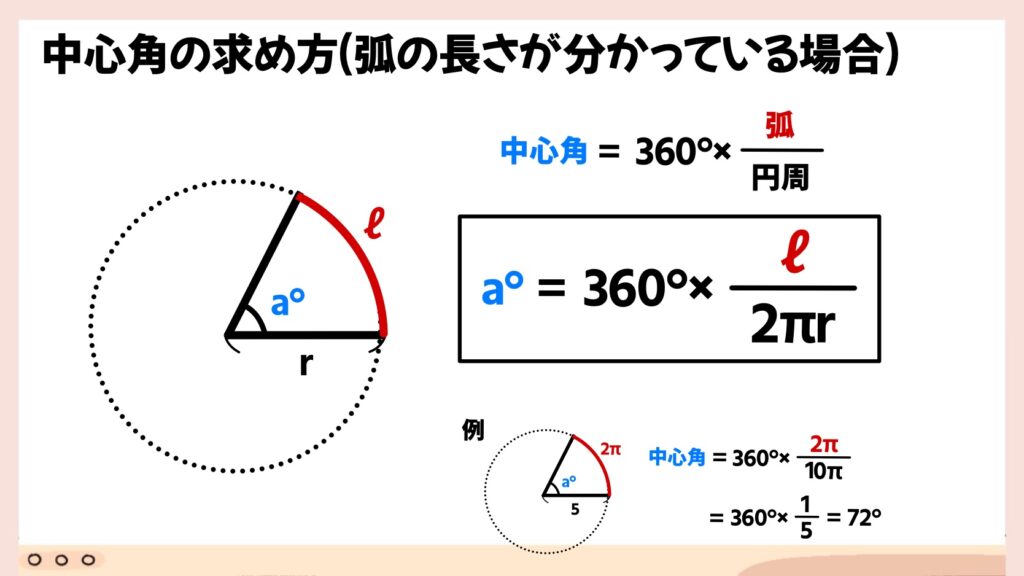
弧の長さから中心角を求める方法を紹介します。

弧の長さが分かっている場合、円周の長さと弧の長さの割合を求めます。例えば、弧の長さが２π㎝、円周の長さが10π㎝だった場合、その割合は5分の1となる。つまり、中心角も360°の5分の1だということが分かるので、72°であることが分かります。

　面積から中心角を求める

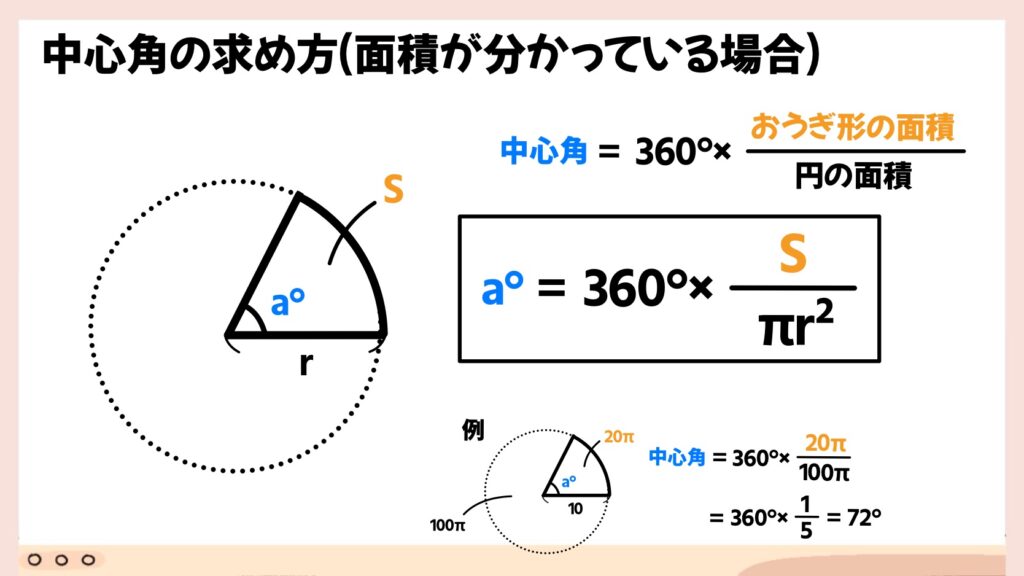
次に面積が分かっている場合の中心角の求め方を紹介します。考え方は弧の長さが分かっている時と変わりません。

扇形の面積が円全体の面積の割合を占めているかを求めます。

例えば、扇形の面積が20π、円全体の面積が100πのとき、割合は5分の1となるので、中心角も360°の5分の1であることが分かります。

　円の面積はなぜ半径×半径×3.14？

　円をケーキのように分ける

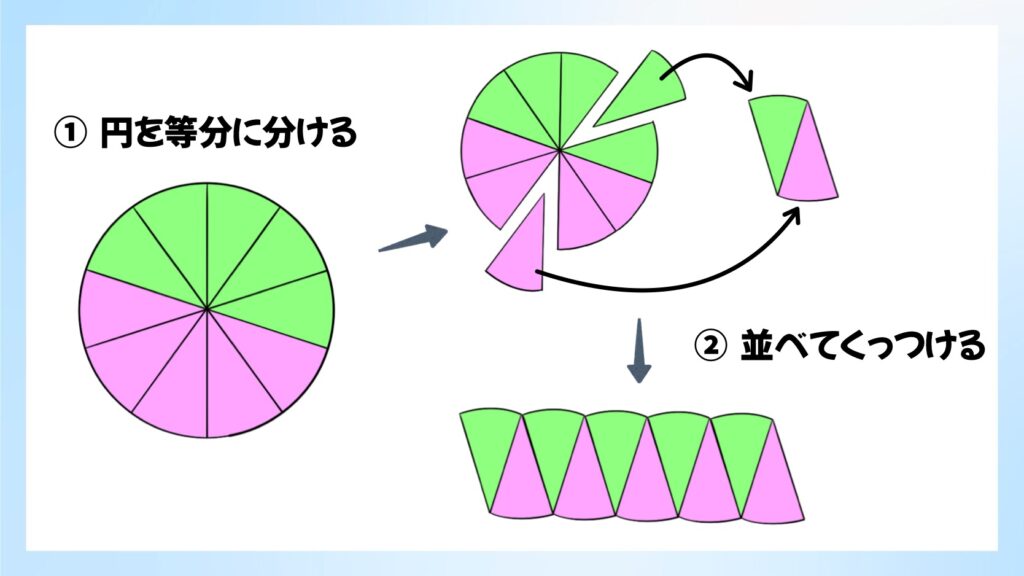
まず図の①のように円を等分に分けます。ここでは分かりやすいように上半分を緑色に、下半分をピンク色に塗りました。

このケーキのようなおうぎ形を、②のように互い違いにくっつけて並べていきます。

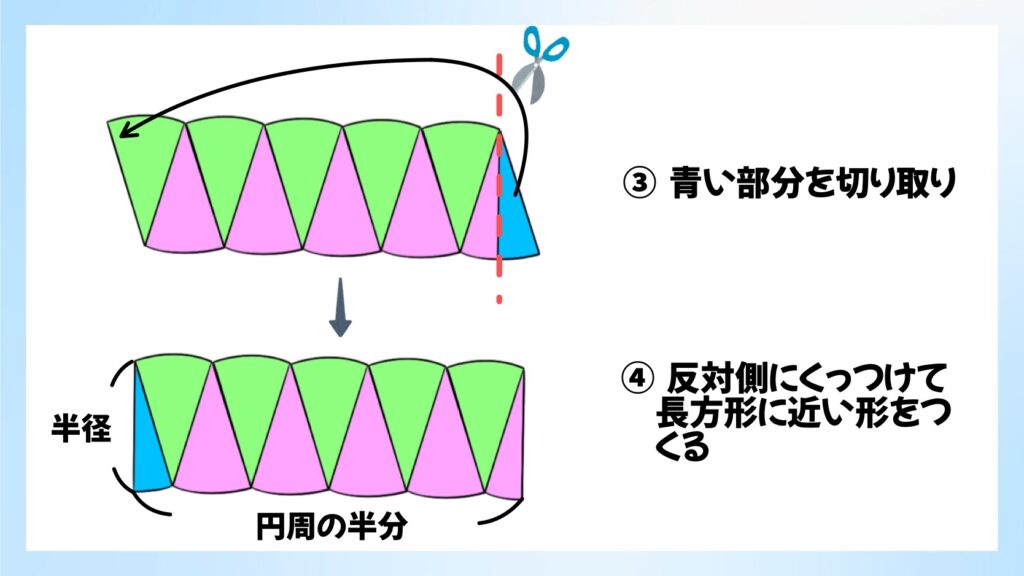
　これを青い部分で切り取り、反対側にくっつけると、長方形に近い形になります。（青い部分を切り取らずに、平行四辺形の形として考えても良い。）

　切り取るおうぎ形を細かくしていくと…

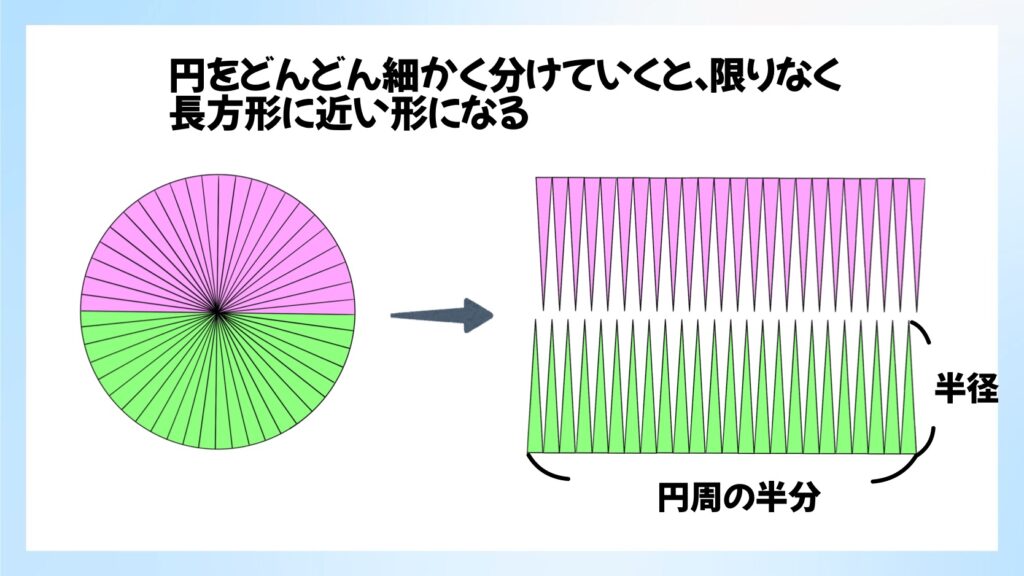
　上のような作業を、円をどんどんと細かく分けていきます。図では48個に分けていますが、もっともっと細かくしていくと、限りなく長方形に近い図形になります。

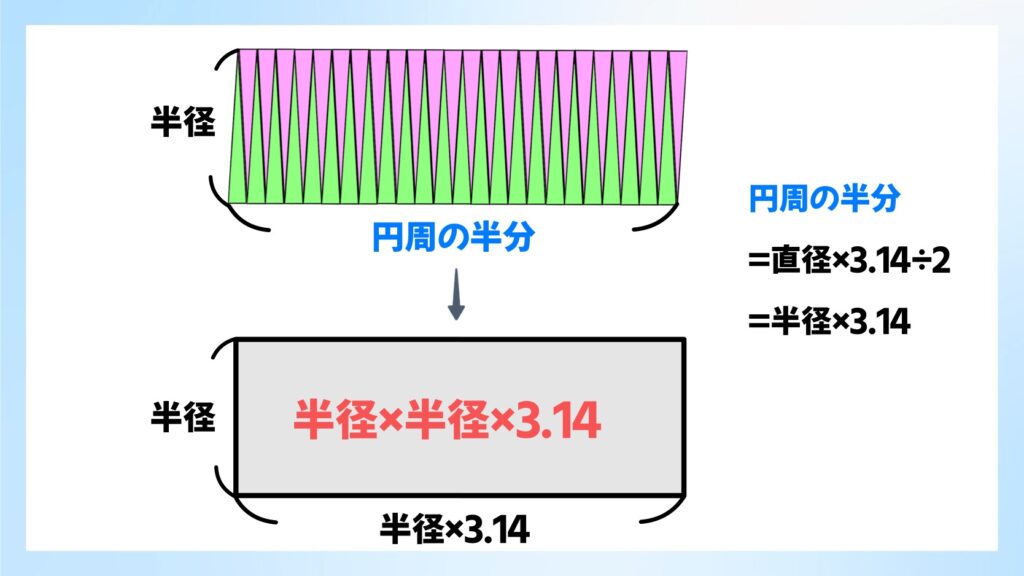
　円からできた長方形の「タテ」の長さは半径と同じ長さで、「ヨコ」の長さは円周の半分の長さになります。

　「円周の半分の長さ」＝「直径×3.14÷２」＝「半径×3.14」となる。

　長方形の面積は「タテ×ヨコ」なので、「半径×半径×3.14」となります。

　なぜ円周率は3.14？

　そもそも円周率って何？

円周率は小学生の時は3.14で習い、中学生になるとπ（パイ）を使いますよね。円周率は円の外周の長さ（円周）と、その円の直径の長さの比率を表す数字です。直径が１㎝の円だとすると、その円周の長さは約3.14㎝となります。

円周：直径 × 円周率（3.14）

つまり、どんな大きさの円でも、円周を直径で割ると3.14になります。直径が２㎝であれば円周は6.28…㎝、直径が３㎝であれば円周は9.42…㎝となっていきます。この特別な数字が円周率と呼ばれ、実際には小数点が続く無限の数字です。

　誰が発見したの？

円周率を発見したのは、古代ギリシャの数学者であるアルキメデスが発見したと言われています。

アルキメデスは紀元前287年～212年頃の最も天才的な数理科学者で、シチリア島で生まれたとされています。今では分数や小数などを量としてあたり前のように数として認識して、自由に四則演算ができるようになったのも、アルキメデスのような大天才が多くの知見を残してくれたおかげなのです。

以下ではアルキメデスがどのように３．１４を発見したのか紹介していきます。

　３．１４を求めてみる

アルキメデスが約４０００年前に円周率３．１４求めたやり方を紹介します。

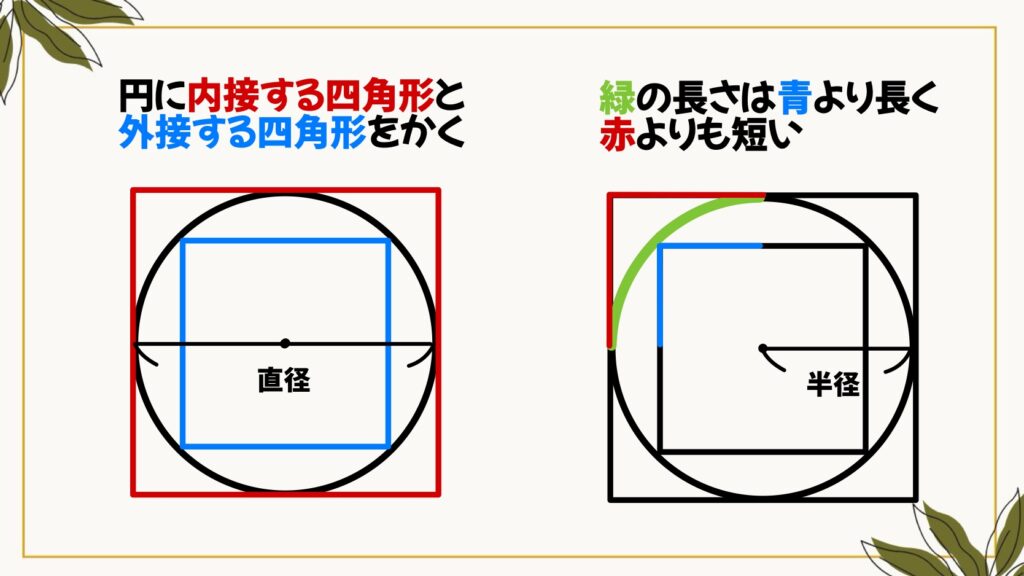
まず、円の内側にぴったりはまる（内接する）青い正方形と、外側に円の直径がぴったりとはまる（外接する）赤い正方形をかきます。

画像の右側のように、緑の部分は青の部分より長く、赤い部分よりも短くなります。（青＜緑＜赤）

つまり、円周の長さは内側の正方形の周の長さよりも長く、外側の正方形の周の長さよりも短くなることが分かります。

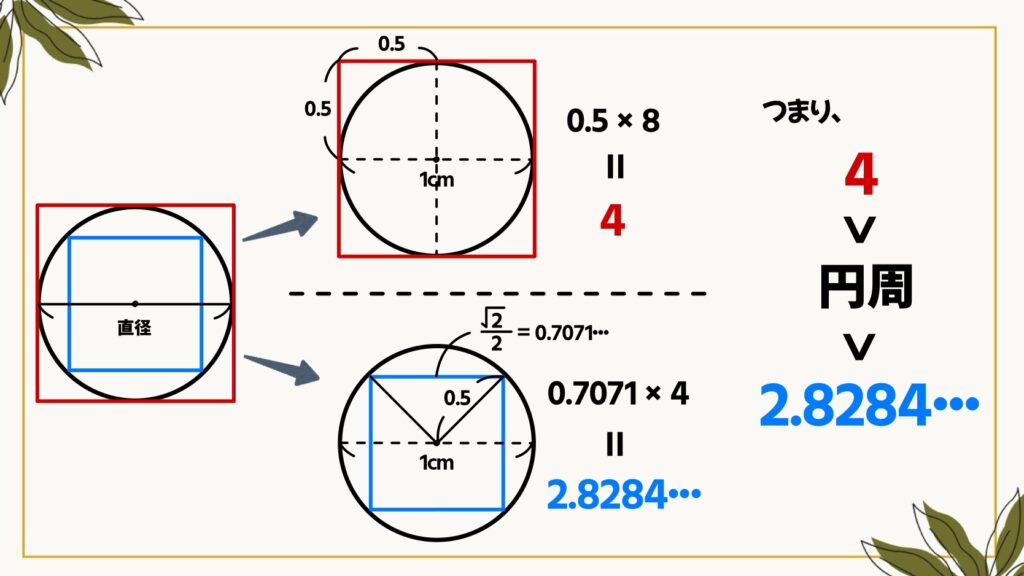
円の直径を１㎝とすると、外側の正方形の周の長さは８㎝となります。内側の正方形は、三平方の定理を使うと１辺が√2/2㎝となるので、周の長さは√2/2×4＝2.8284…㎝となります。

よって、円周の長さは2.8284…㎝より大きく、4㎝よりも小さいことが分かります。

2.8284…＜円周＜４

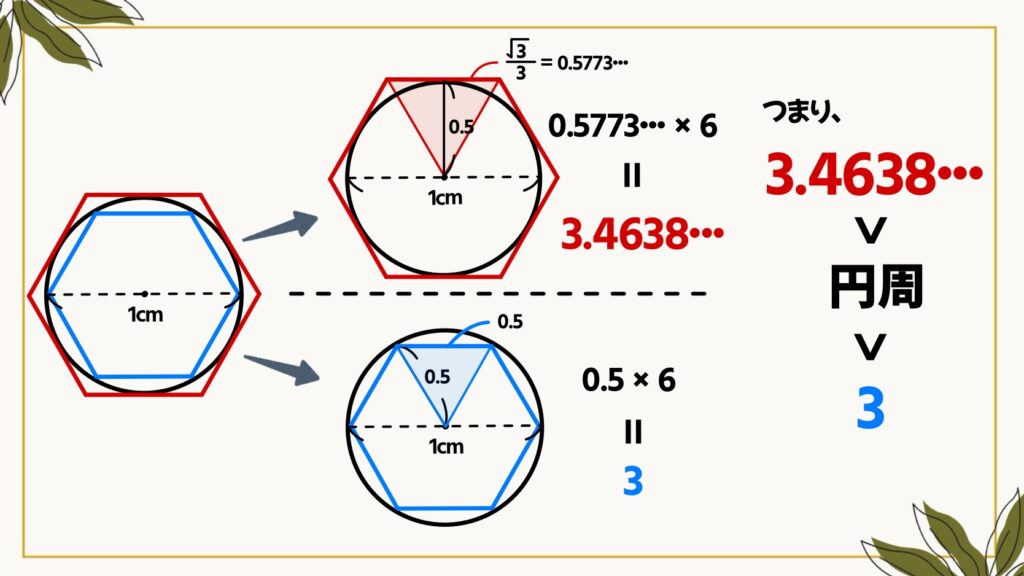
同じように円の中に今度は正六角形をかいてみます。円周の長さは内側の正六角形の周の長さよりも長く、外側の正六角形の周の長さよりも短くなります。

外側の正六角形は、三平方の定理を使うと１辺が√3/3㎝となり、周の長さは√3/3×6＝3.4638…となり、内側の正六角形の周の長さは３㎝となります。

よって、円周の長さは３㎝よりも大きく、3.4638…㎝よりも小さいことが分かります。

３＜円周＜3.4638

もう分かりましたよね？この円にそれぞれ内接、外接する正多角形の角を増やしていくと、円周率は3.14…㎝に近づいていくというわけです。

ちなみに、正１６角形まで調べると、3.14084…＜円周＜3,14286…が分かります。かなり皆さんの知っている円周率に近づいていますよね！

　円周率を確かめてみよう

子供に3.14を教えようと思ったら、上のようなやり方では少し難しいので、もっと簡単に3.14を求めてみましょう。

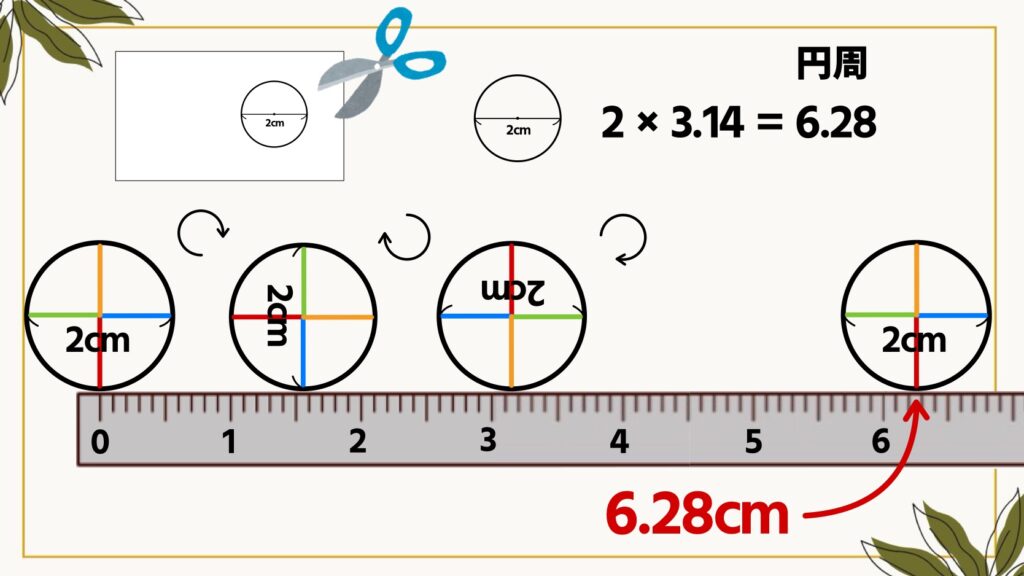
紙にコンパスで円をかきましょう。直径が１㎝、２㎝、３cmの円を３種類ほどかき、ハサミで切り抜いていきます。

切り抜いた円に印をつけて、定規の上で１回転させてみましょう。１㎝の円であれば3.14㎝、2㎝の円であれば6.28㎝、3㎝の円であれば9.42㎝・・・。どれも必ず直径の3.14倍となりますよね。

このやり方であれば、子供でも3.14という数字を少し身近に感じることができるかもしれません。

　なぜひし形の面積は対角線×対角線÷２なの？？

　ひし形ってどんな形？

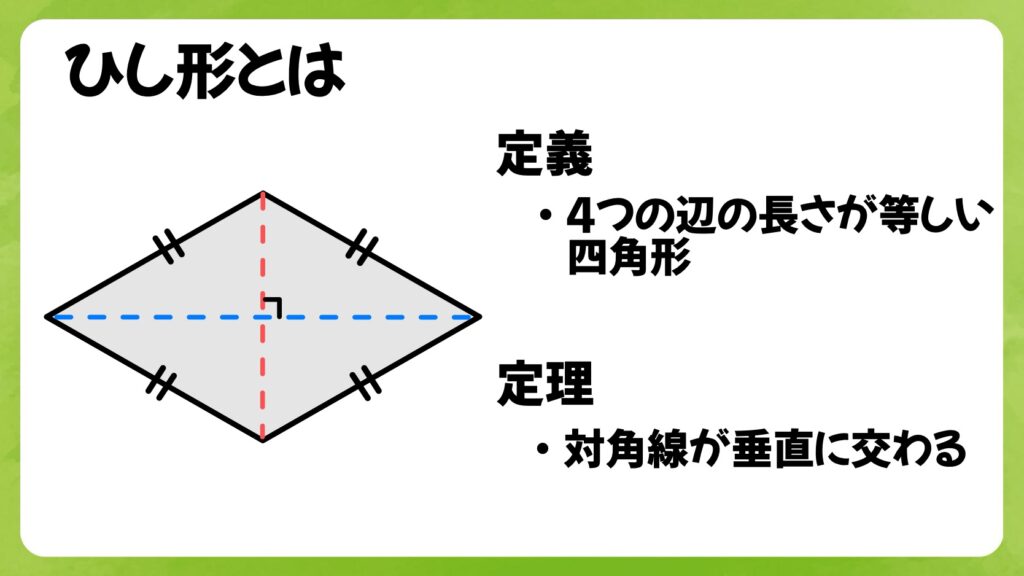
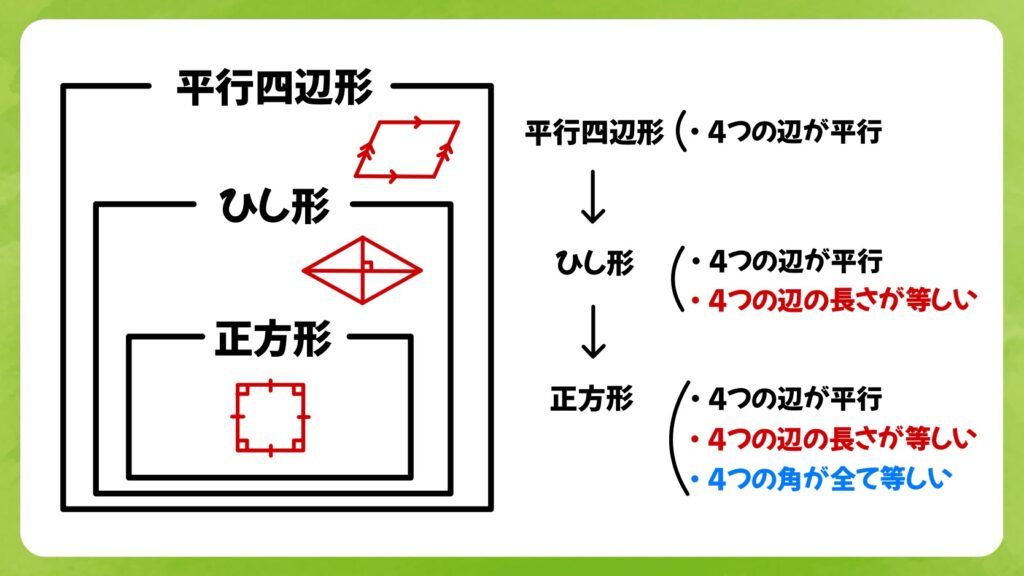
ひし形の定義は「４つの辺の長さが等しい四角形」です。ひし形は、その対角線が互いに直角に交わり、対称性が美しい図形です。ひし形について基本的な特徴をいくつか挙げてみましょう。

１．４つの辺の長さが等しい

　ひし形のもっとも重要な特徴は、４つの辺の長さがすべて等しいことです。この点で、長方形や正方形と似ています。

２．対角線が直角に交わる

　ひし形の対角線は互いに直角に交わります。これは、ひし形を４つの直角三角形に分けることができます。

３．対角線が対称軸となる

　ひし形の対角線は、その対称軸でもあります。つまり、対角線を折り目として折ると、線対称な図形となります。

４．平行四辺形のの性質を持つ

　ひし形は平行四辺形の性質を持ち、正方形はひし形と平行四辺形両方の性質を持つ。

　ひし形の面積の公式

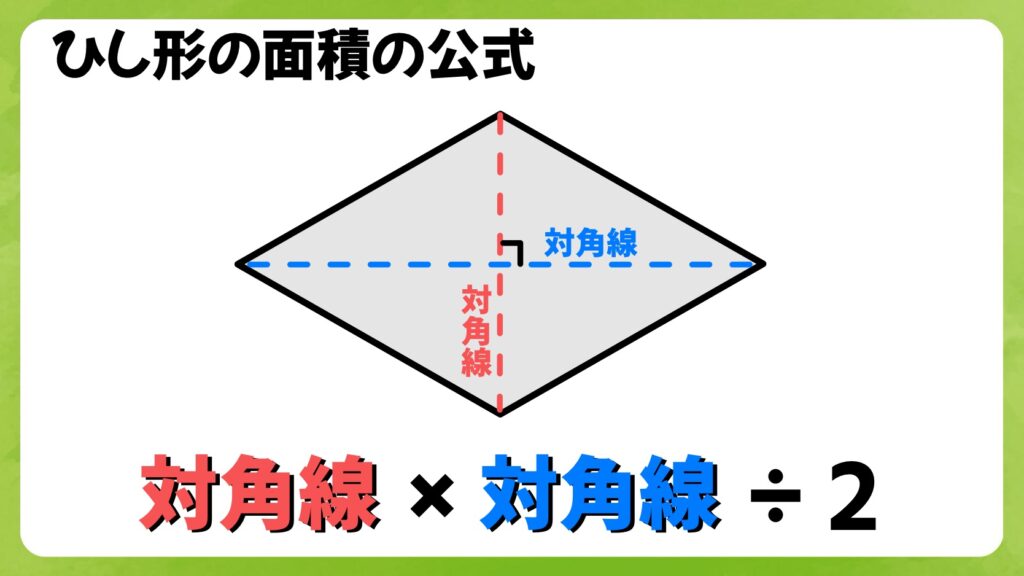
ひし形の面積の公式は「対角線×対角線÷２」です。ひし形は数学のテストにあまり出てこないことから、この公式を知っている人はそんなに多くないかもしれませんね。

また、なぜこの公式で面積が求めることができるのか知っている人は更に少ないでしょう。

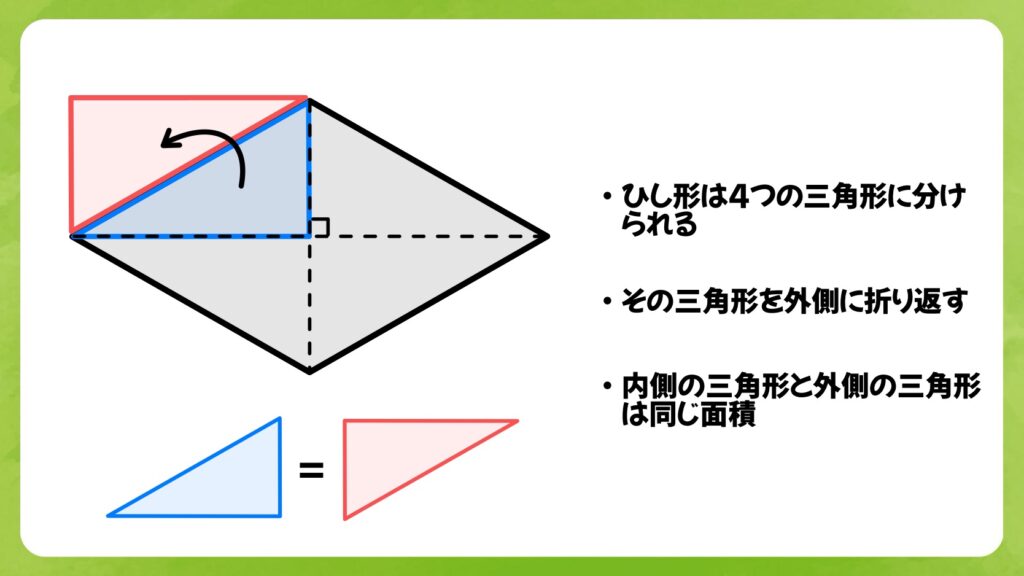
ひし形は４つの直角三角形に分けることができ、４つの三角形を外側に折り返します。図のように、赤い三角形と青い三角形は同じ面積になります。

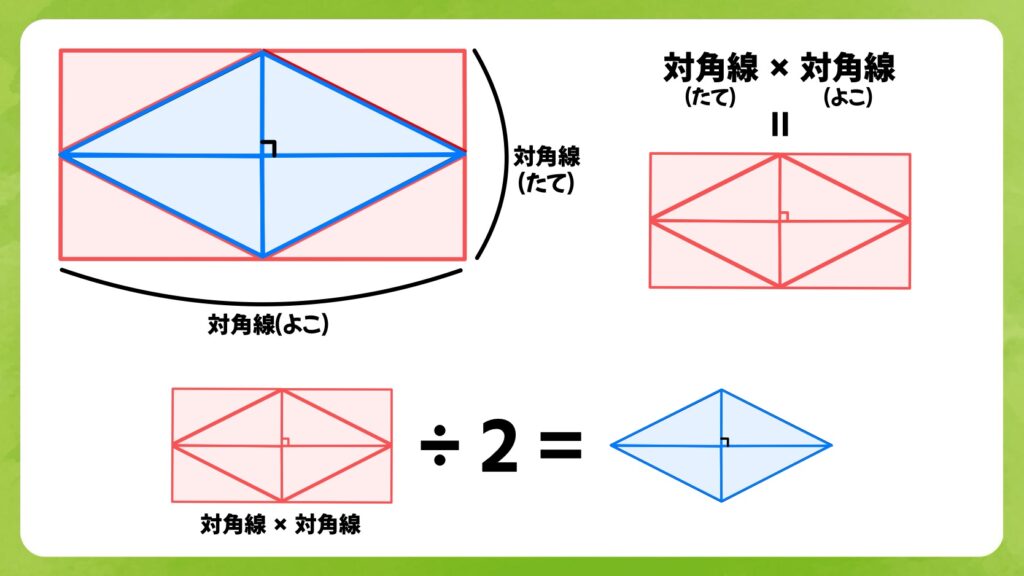
４つの三角形を外側に折り返すと、長方形ができます。この長方形の面積はタテ×ヨコで求めることができます。

長方形のタテ×ヨコはひし形で言うと「対角線×対角線」となります。青いひし形の面積は、長方形全体の面積の半分となるので、ひし形の面積は「対角線×対角線÷２」で求めることができます。

　なぜ台形の面積は（上底＋下底）×高さ÷２なの？

　台形って？

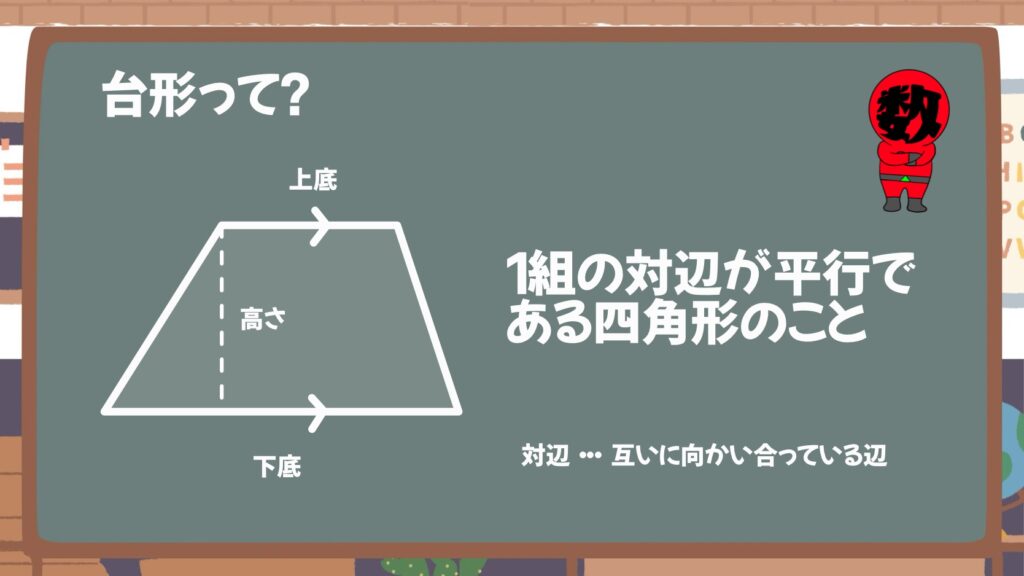
台形は四角形の一種で、１組の対辺が互いに平行である四角形のことをいいます。

平行な２本の対辺を台形の底辺といい、そのうちの一方を「上底」、もう片方を「下底」といいます。

　台形の種類

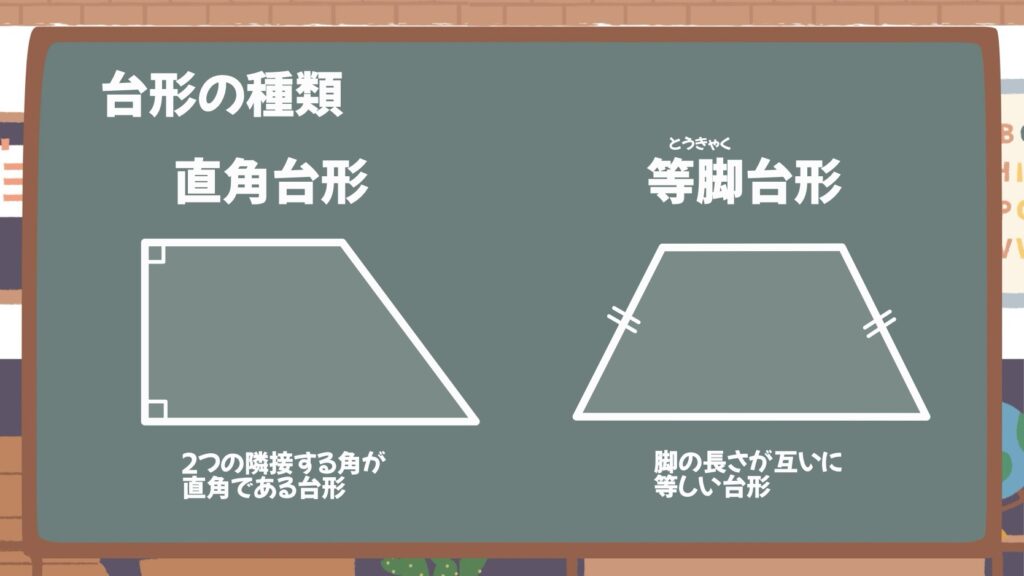
　台形のうち、４つの内角のうち、２つの隣接する角が直角である台形を直角台形、下底の両端にある２つの内角が（底角）が等しく、足の長さが等しい台形の事を等脚台形といいます。

　台形の面積の求め方の説明①

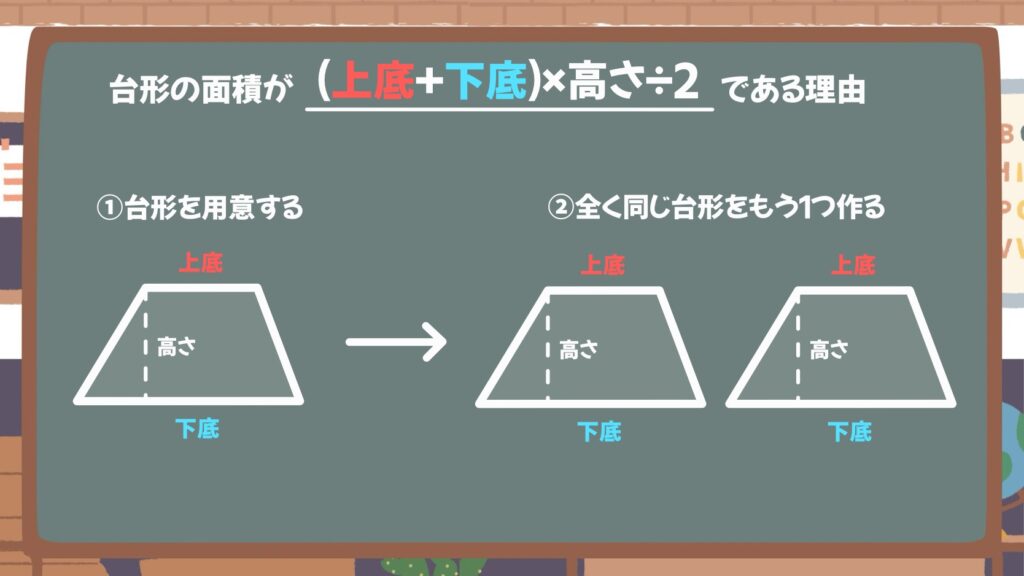
まずは台形を１つ用意します。その台形と全く同じ台形をもう１つ作ります。

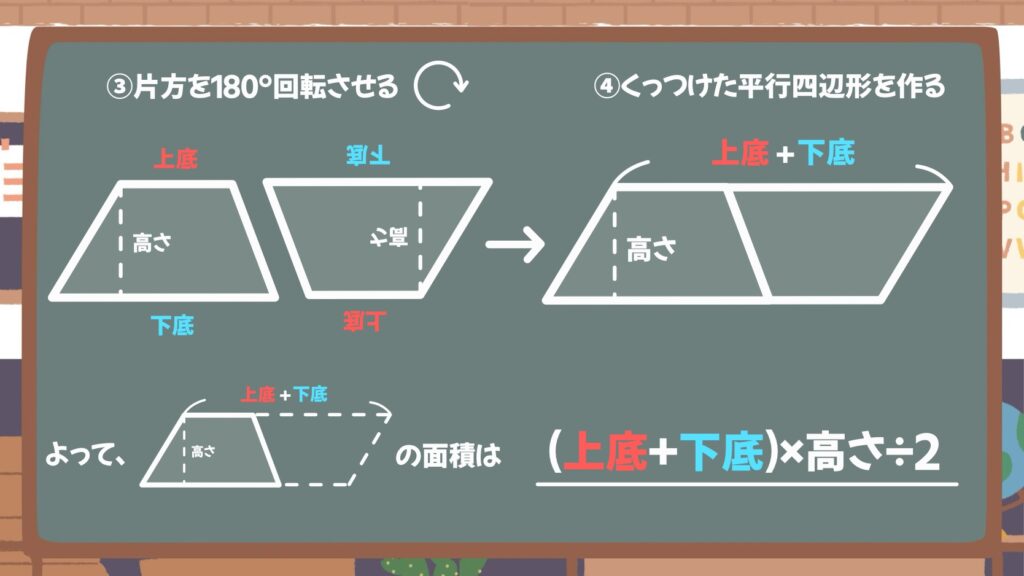
片方の台形を180°回転させてからくっつけると、１つの平行四辺形ができます。

この平行四辺形の１辺は（上底＋下底）となり、高さをかけるとこの平行四辺形の面積を求めることができます。

求めた平行四辺形の半分が台形の面積なので、（上底＋下底）×高さ÷２で求められることが分かります。

　台形の面積の求め方の説明②

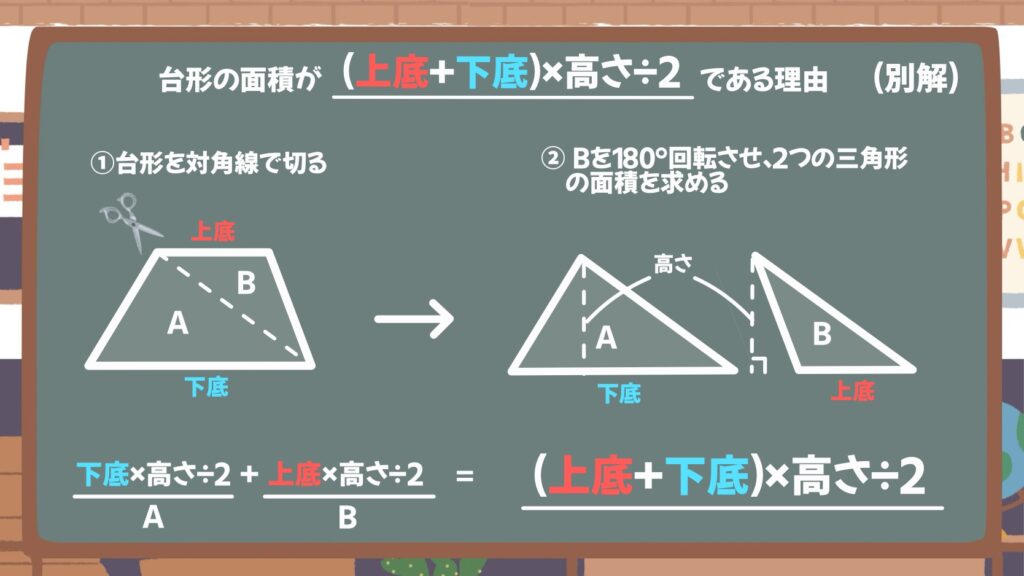
他の方法を紹介します。

台形を対角線で切断します。片方を180°回転させると、Ａの三角形は下底×高さ÷２、Ｂの三角形は上底×高さ÷２で求められるので、台形の面積は下底×高さ÷２＋上底×高さ÷２＝（上底＋下底）×高さ÷２で求められることが分かりますね。

　分数の割り算はなぜ逆数にするの？

　図で理解しよう

まずは６÷２で考えましょう。誰もが答えは３であることは分かります。おそらく多くの人が２×〇＝６で、〇に入る数字は３だから、答えは３！と考えたのではないでしょうか？

次に、６÷２＝３を水を使って具体的に考えてみましょう。

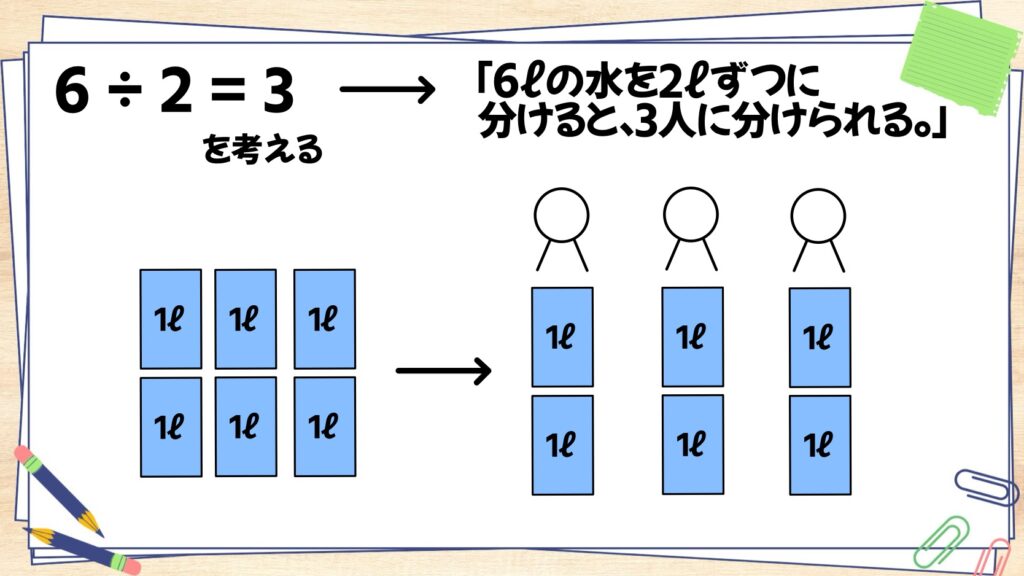
６÷２＝３を「６ℓの水を２ℓずつに分けると、３人に分けられる。」と考えると、下の図のようになりますよね。

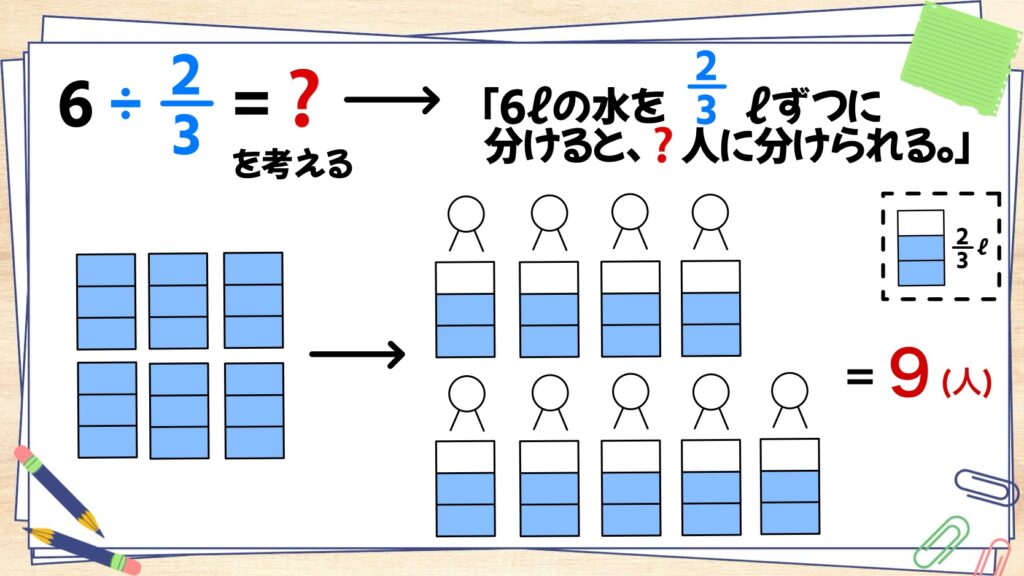
６÷２/３＝？を考えましょう。上と同じように具体的に考えうと「６ℓの水を２/３ℓずつ分けると、？人分けられる。」と考えます。実際に分けてみると、下の図のように、９人に分けることができることが分かります。

つまり、６÷２/３＝９であることが分かりますね。

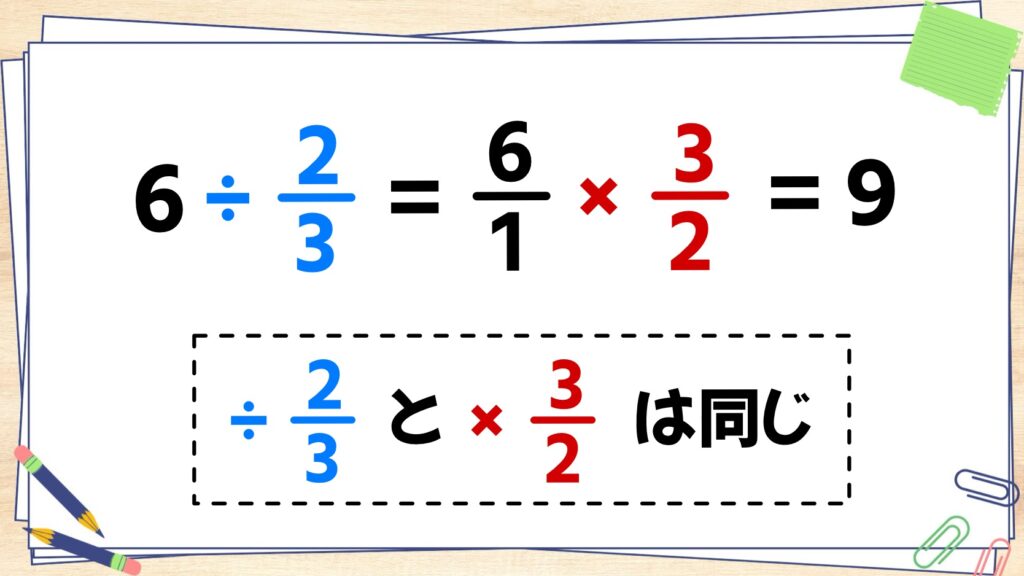
６に何をしたら９になるかを考えると、６×３/２＝９となることが分かるので、÷２/３と×３/２は同じということが言えますね。

「割り算→分数」の変型で考える

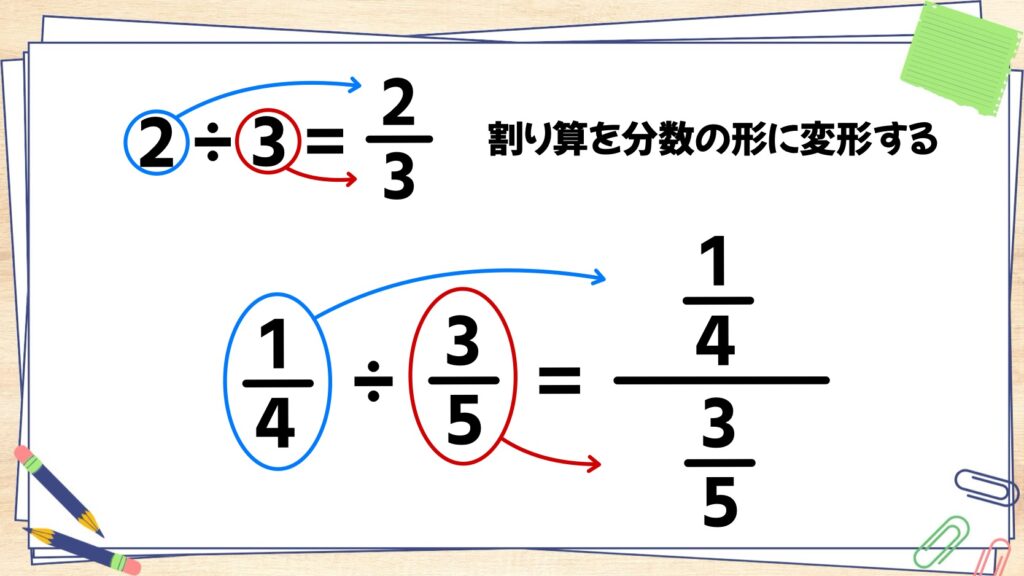
２÷３＝２/３のように、割り算は分数に変形することができます。これを分数の割り算で考えてみましょう。

１/４÷３/５を分数の形に直してみると、下の図のように変形することができます。この「分数の分数」の形を「繁分数」といいます。

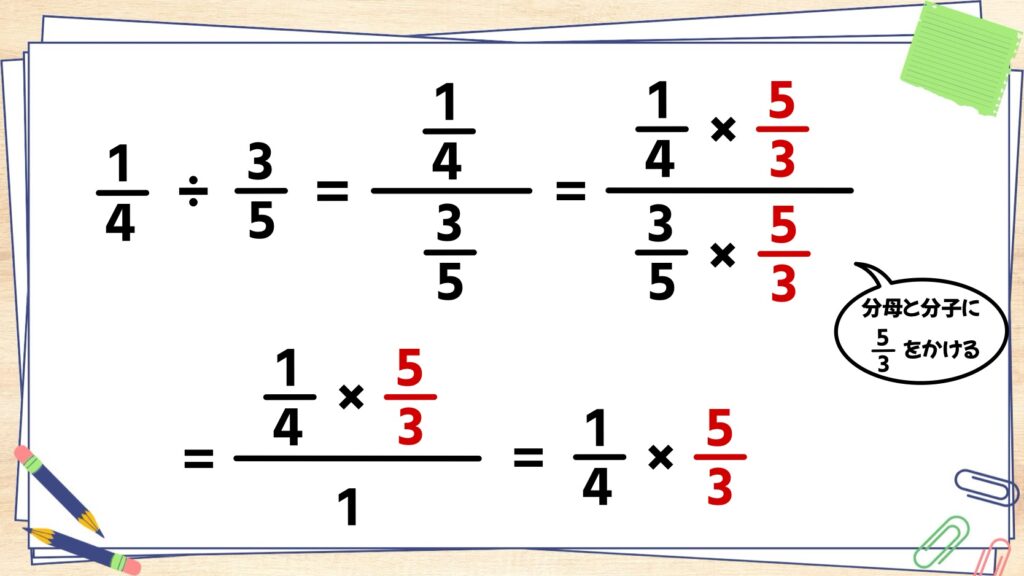
分数は、分母と分子に同じ数をかけても数が変わらないという性質があります。この性質を使って、１/４分の３/５の分母と分子にそれぞれ５/３をかけます。

計算すると、分母が１になり、分子が１/４×５/３となります。結果的に、１/４÷３/５=１/４×５/３となります。