【保存版】小中学校で習う算数・数学の公式一覧｜これだけ覚えれば大丈夫！

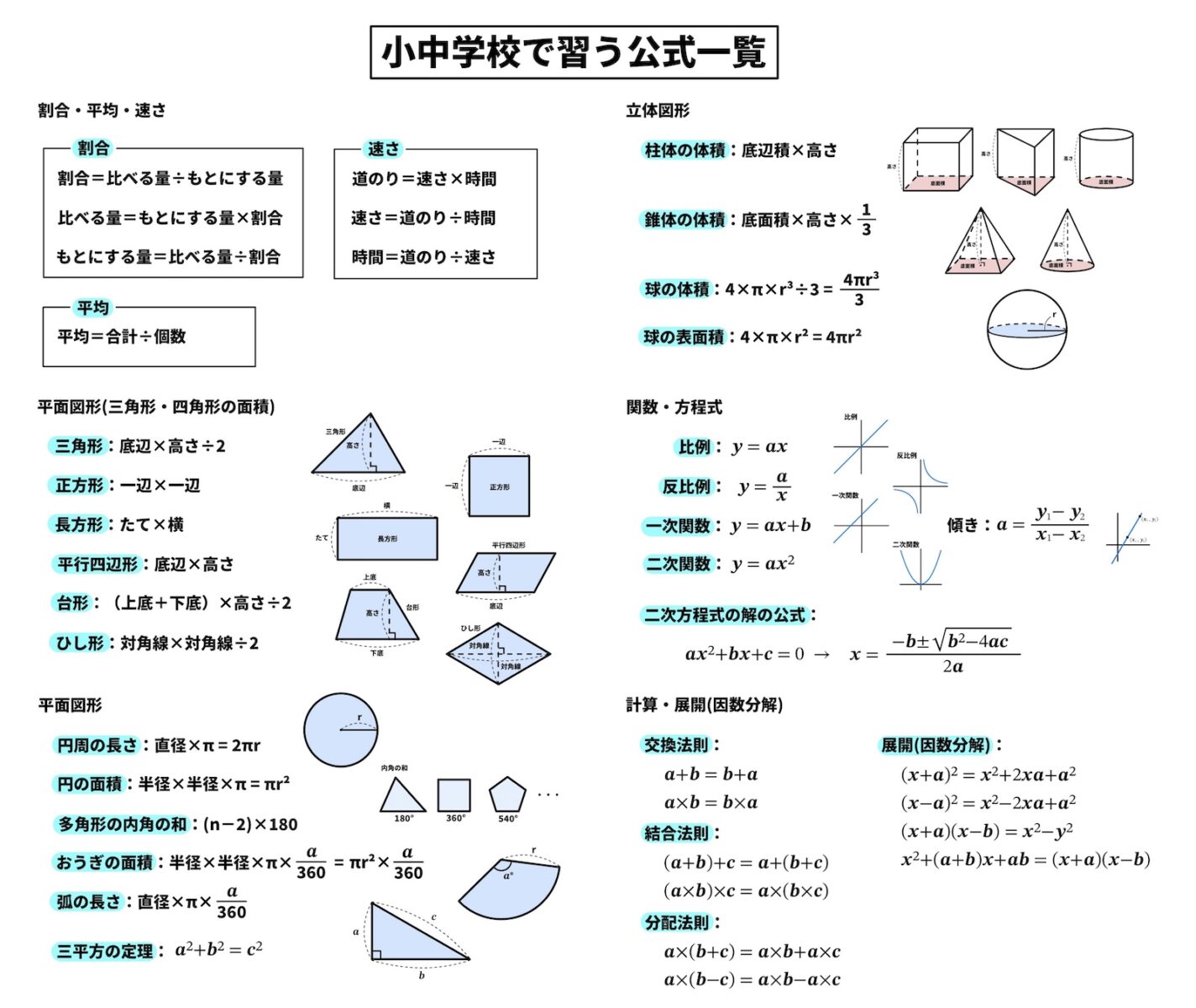
算数や数学の学習では、「公式」を覚えることがとても大切です。面積や体積、速さ、関数…と単元ごとにたくさん出てきますが、「どこで何を習ったか分からなくなる」という声もよく聞きます。
そこでこの記事では、小学校から中学校で習う主要な公式を1ページにまとめて一覧化しました。

「こんなにあるんだ！」と驚くと同時に、「これだけ覚えれば大丈夫」と安心できる内容になっています。テスト前の確認、授業準備、家庭学習のサポートなど、さまざまな場面で使える保存版公式集です。
各公式には短い説明と図を添えているので、中学生はもちろん、小学生や保護者、先生にも役立ちます。

論理的思考力を鍛えるクイズ５０問！

↑↑↑子供の学習や大人の脳トレに最適！！

割合・平均・速さ

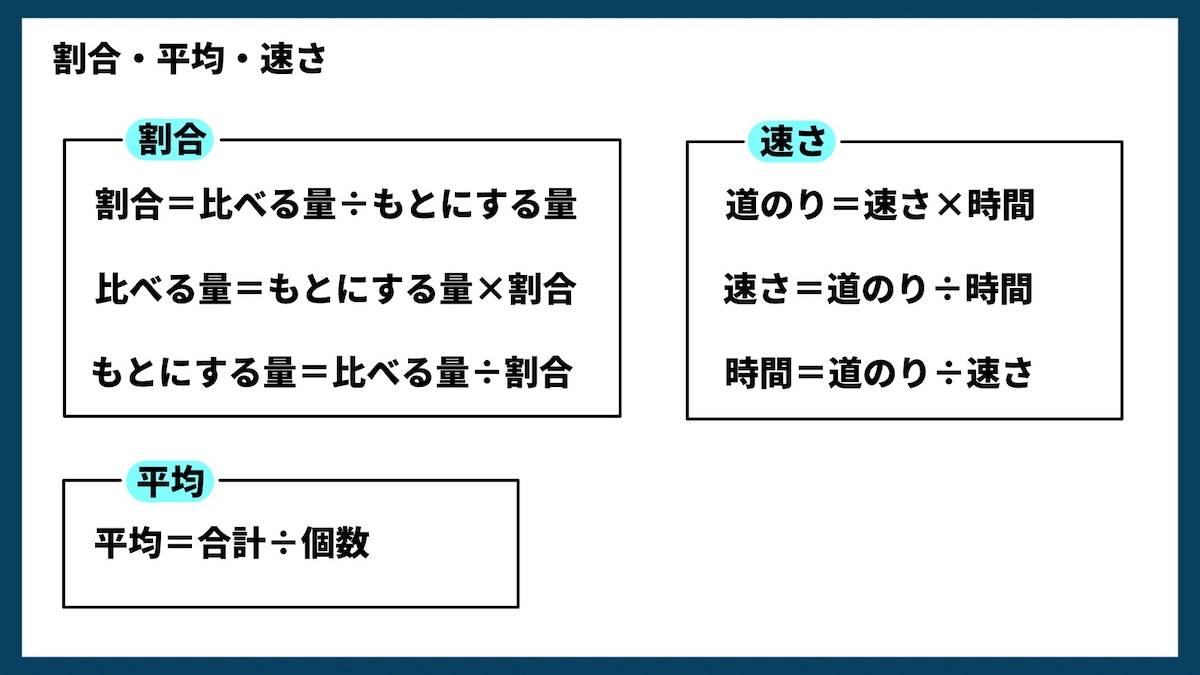
割合

割合は、ある量が基準（もとにする量）に対してどれくらいの大きさかを表すものです。
割合 ＝ 比べる量 ÷ もとにする量

例えば、テストで80点を取ったとき、満点が100点なら
割合＝80 ÷ 100＝0.8（80％）
となります。割合は百分率（％）や小数で表せるので、状況に応じて使い分けましょう。

---

平均

平均は、全体の合計を人数や個数で割った値です。
平均 ＝ 合計 ÷ 個数

例えば、テストの点数が80点、90点、100点の3人がいた場合、
平均＝（80＋90＋100）÷ 3 ＝ 90
となります。平均はデータの代表的な値として、統計や日常生活でもよく使います。

---

速さ

速さは、一定時間に進む距離のことです。次の3つの式は必ずセットで覚えましょう。

• 速さ ＝ 道のり ÷ 時間
• 道のり ＝ 速さ × 時間
• 時間 ＝ 道のり ÷ 速さ

例えば、「時速60kmで2時間走った」ときの道のりは
道のり＝60 × 2 ＝ 120km
となります。距離・時間・速さの関係は比例・反比例の学習にもつながる重要な内容です。

平面図形（三角形・四角形の面積）

平面図形の面積は、形によって計算方法が異なります。ここでは三角形と四角形の代表的な公式を紹介します。すべて覚えておくと、テストや日常生活でも役立ちます。

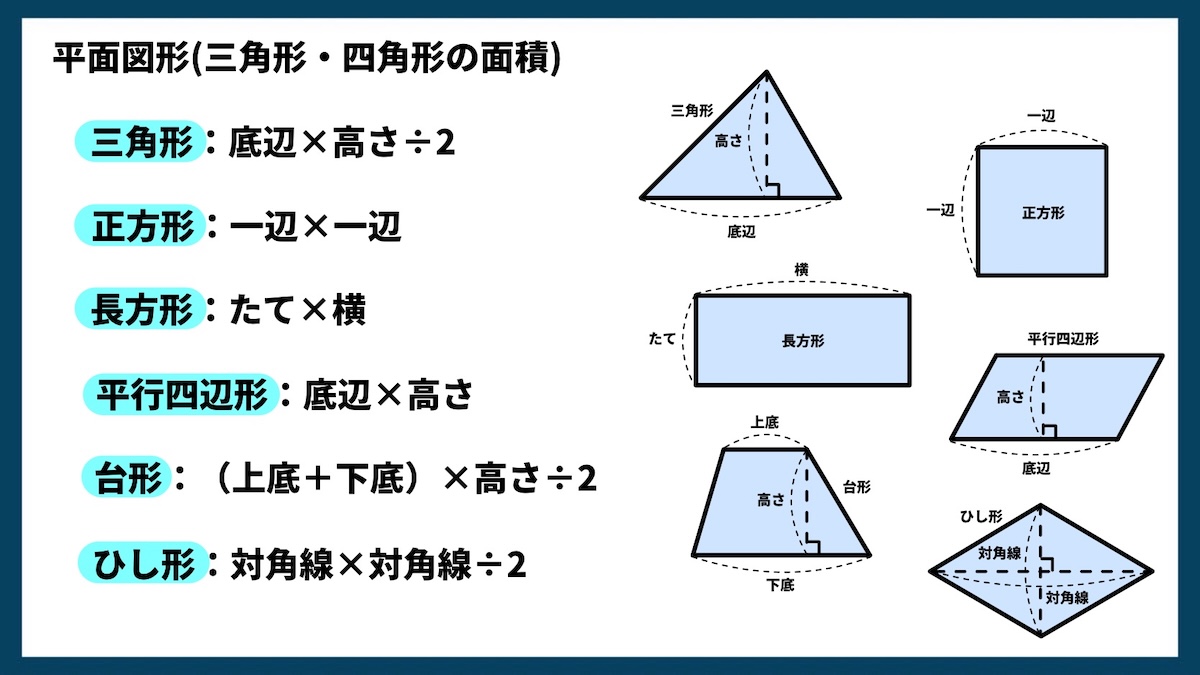
三角形

底辺 × 高さ ÷ 2
三角形の面積は、同じ底辺と高さを持つ長方形の半分になります。高さは、底辺の反対側にある角から垂直に下ろした線の長さを使います。

---

正方形

一辺 × 一辺
すべての辺の長さが同じなので、一辺の長さをかけ算すれば面積が求められます。

---

長方形

たて × 横
学校で最初に習う面積の公式。辺の長さをかけるだけで求められます。

---

平行四辺形

底辺 × 高さ
形が斜めでも、底辺に垂直な高さを使えば面積が求められます。長方形と同じ公式です。

---

台形

（上底 ＋ 下底） × 高さ ÷ 2
上の辺と下の辺の長さを足して高さをかけ、最後に2で割ります。長方形と三角形を組み合わせた形として考えると覚えやすいです。

---

ひし形

対角線 × 対角線 ÷ 2
2本の対角線の長さをかけて2で割ります。対角線で分けた三角形が4つできるイメージです。

平面図形

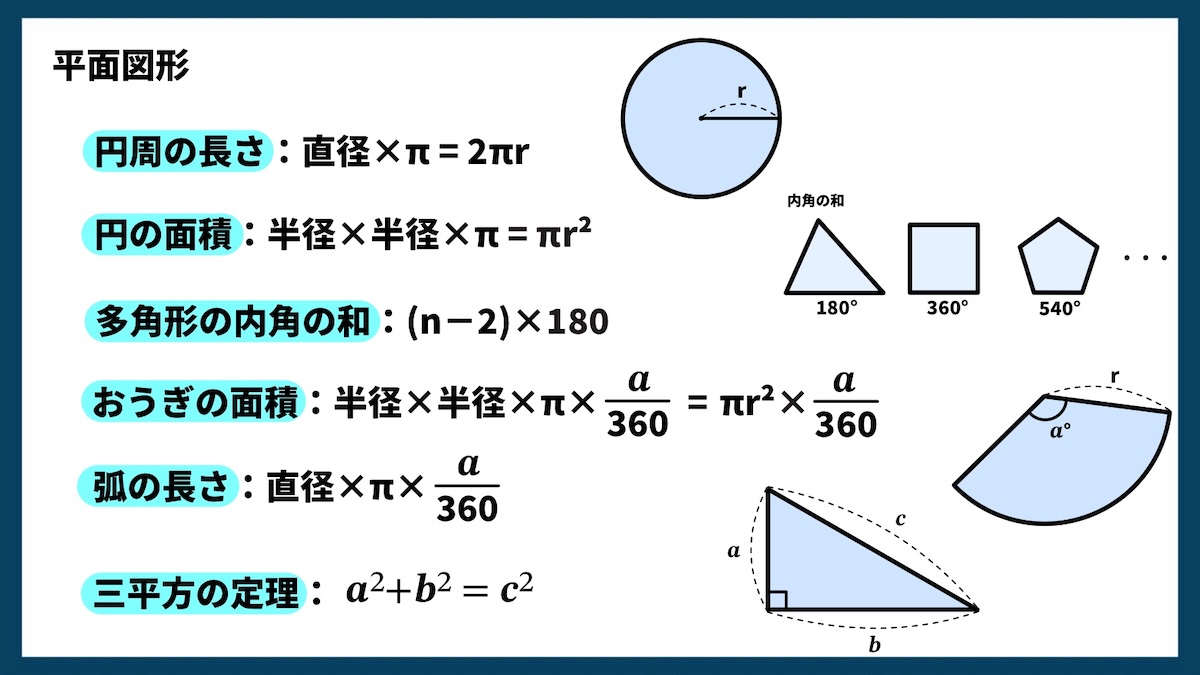
円周の長さ

直径 × π または 2 × 半径 × π
円の外周の長さを求める公式です。直径に3.14をかけるか、半径に2をかけてから3.14をかけても同じ結果になります。

---

円の面積

半径 × 半径 × π
半径を2回かけた値に3.14をかけます。半径が10cmなら、10 × 10 × 3.14 ＝ 314cm² です。

---

多角形の内角の和

（辺の数 − 2） × 180
三角形の内角の和は180°、四角形は360°、五角形は540°…と増えていきます。この公式で一度に求められます。

---

扇形の面積

半径 × 半径 × π ×（中心角 ÷ 360）
円全体の面積に、中心角が何度分かをかけて求めます。例えば半径6cm、中心角90°の扇形なら、6 × 6 × 3.14 ×（90 ÷ 360）＝ 28.26cm² です。

---

弧の長さ

直径 × π ×（中心角 ÷ 360）
円周の長さに、中心角が何度分かをかけて求めます。90°なら円周の4分の1の長さになります。

---

三平方の定理

a² ＋ b² ＝ c²
直角三角形で、直角をはさんだ2辺をaとb、斜めの辺（斜辺）をcとすると、この関係が成り立ちます。例えば、a＝3cm、b＝4cmなら、c²＝9＋16＝25なので、c＝5cmです。

立体図形

立体の体積や表面積は、底面積や高さ、半径などの値をもとに計算します。形によって公式が異なるので、1つずつ覚えておきましょう。

---

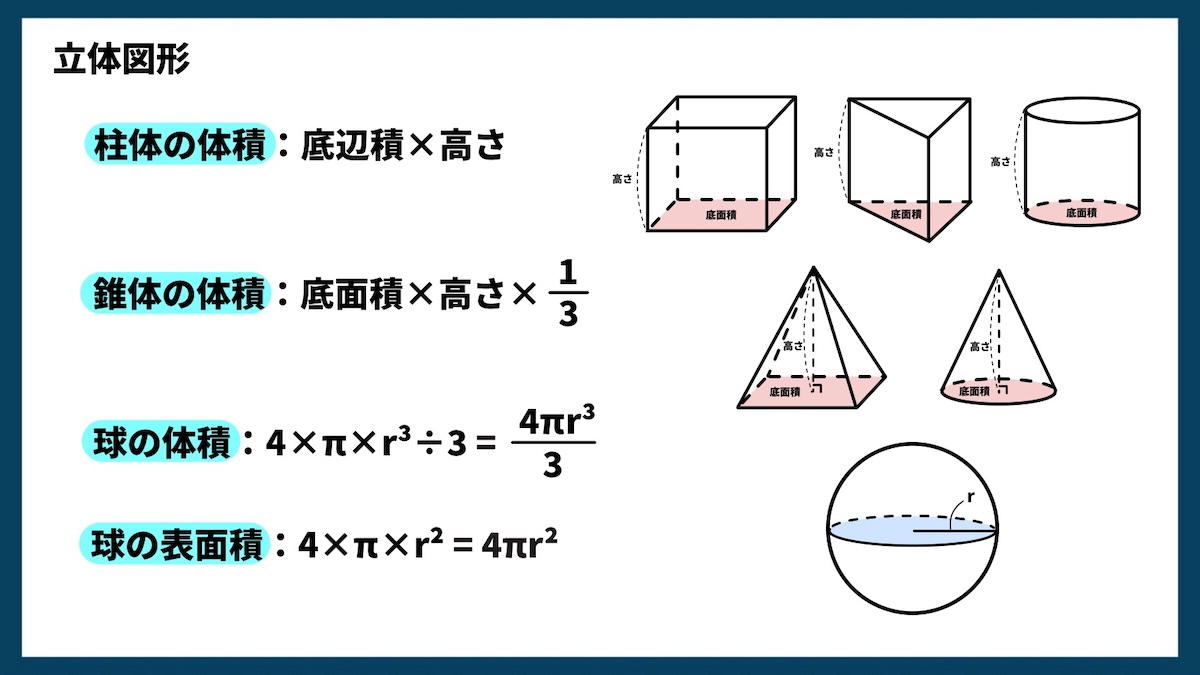
柱体の体積（直方体・立方体・円柱など）

底辺積 × 高さ
底面が四角形でも円でも同じ公式です。底面積を求めてから高さをかけます。
例：円柱の体積＝（半径 × 半径 × π）× 高さ

---

錐体の体積（角すい・円すい）

底面積 × 高さ × 1/3
柱体の体積の3分の1になります。
例：円すいの体積＝（半径 × 半径 × π）× 高さ × 1/3

---

球の体積

4 × π × 半径³ ÷ 3
半径を3回かけた値に4πをかけ、3で割ります。

---

球の表面積

4 × π × 半径²
半径を2回かけた値に4πをかけます。

関数・方程式

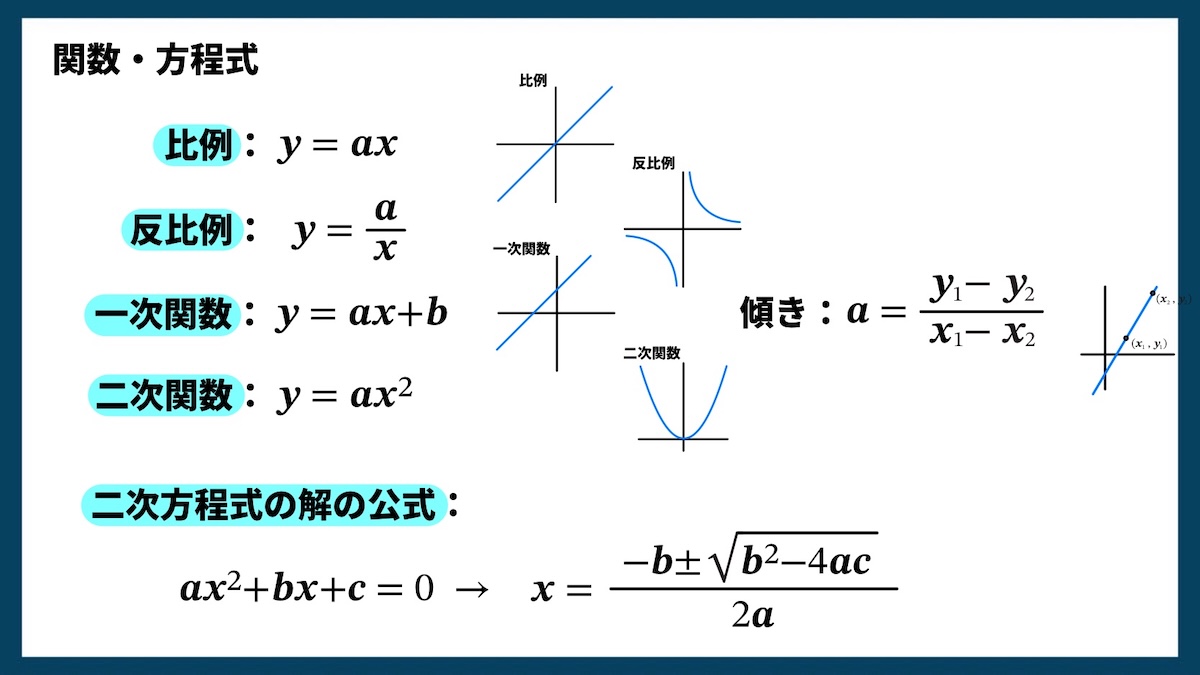
関数や方程式の公式は、中学校の数学でとても重要な内容です。グラフの形や式の関係を理解すると、問題がぐっと解きやすくなります。

---

比例

𝒚＝𝒂 ×𝒙
xが2倍になればyも2倍になる関係。グラフは原点を通る直線になります。

---

反比例

𝒚＝𝒂 ÷𝒙
xが大きくなるとyが小さくなり、xが小さくなるとyが大きくなる関係。グラフは曲線（双曲線）になります。

---

一次関数

𝒚＝𝒂𝒙+𝒃
直線の式。aは傾き、bは切片を表します。傾きは次の公式で求められます。
𝒂 ＝（y₂ − y₁）÷（x₂ − x₁）

---

二次関数

𝒚＝𝒂 ×𝒙²
放物線の形をしたグラフになります。aの値が正だと上に開き、負だと下に開きます。

---

二次方程式の解の公式

𝒂 ×𝒙²＋𝒃×𝒙＋𝒄 ＝0 のとき
𝒙 ＝｛−𝒃 ± √（𝒃 ² − 4×𝒂×𝒄 ）｝÷（2×𝒂 ）
因数分解や平方完成で解けないときに使う便利な公式です。

計算・展開（因数分解）

計算の基礎となる3つの法則と、展開・因数分解の代表的な公式です。文字式の計算や方程式の変形で何度も使います。

---

交換法則

順番を入れ替えても結果は変わりません。

• 𝒂 ＋𝒃 ＝𝒃 ＋𝒂
• 𝒂 ×𝒃 ＝𝒃 ×𝒂

---

結合法則

かっこの位置を変えても結果は変わりません。

• （𝒂 ＋𝒃 ）＋𝒄 ＝𝒂 ＋（𝒃 ＋𝒄 ）
• （𝒂×𝒃 ）×𝒄＝𝒂 ×（𝒃×𝒄 ）

---

分配法則

かけ算が足し算や引き算に分配されます。

• a×（b＋c）＝a×b＋a×c
• a×（b−c）＝a×b−a×c

---

展開公式（因数分解）

• （𝒙 ＋𝒂 ）²＝𝒙 ²＋2×𝒙×𝒂 ＋𝒂 ²
• （𝒙−𝒂 ）²＝𝒙 ²−2×𝒙 ×𝒂＋𝒂 ²
• （𝒙＋𝒂 )(𝒙−𝒃 ）＝𝒙²−𝒚 ²（※y＝bの場合）
• 𝒙 ²＋（𝒂 ＋𝒃）×𝒙 ＋𝒂×𝒃 ＝（𝒙＋𝒂)(𝒙＋𝒃 ）

これらの公式は、式を展開する場合だけでなく、逆にまとめる（因数分解）ときにも使えます。

まとめ

小学校から中学校までに習う算数・数学の公式を、ジャンル別にまとめて紹介しました。
公式は覚えるだけでなく、どんな場面で使うのか理解することが大切です。意味や使い方を意識しながら学べば、問題を解くスピードも正確さもアップします。

この記事を見れば「こんなにたくさんあるんだ！」と驚くかもしれませんが、逆に言えばここに載っている公式をしっかり押さえれば大丈夫ということです。
テスト前の確認、授業準備、家庭学習のサポートなど、さまざまな場面で何度も見返して活用してください。

最後に、記事内の公式画像はまとめて1枚にした一覧版も用意できます。印刷して机の横や教室に貼っておけば、いつでも確認できる「自分専用の公式集」になります。ぜひ有効に活用してください。

論理的思考力を鍛えるクイズ５０問！

↑↑↑子供の学習や大人の脳トレに最適！！