最小公倍数と最大公約数って、名前が似ていることもあって、どっちがどっちだか分からなくなってしまいませんか？
実際、小学校５年生で習うものですが、小６の児童に出題しても、正解率は４割といったところでしょう。中学校１年生に出題しても、５割の生徒が正解すれば良い方じゃないでしょうか？算数が得意な子も、混乱してしまうんですよね。
結論から言うと、最小公倍数と最大公約数の求め方は２通りです。
最小公倍数と最大公約数の求め方
- 倍数・約数を書き出して求める
- 連除法（はしご算）を使って求める
この記事では、最小公倍数と最大公約数の求め方を、イラストを使って分かりやすく解説しています。この記事に載っている画像をスライドのようにして子どもに見せて教えることもできます！それではどーぞ！
小中学校で算数、数学を教えた経験のある僕が分かりやすく解説しました！
担任の僕に、初対面で敵意をむき出しにする生徒が半年で変わった理由！
倍数と約数を説明できる？
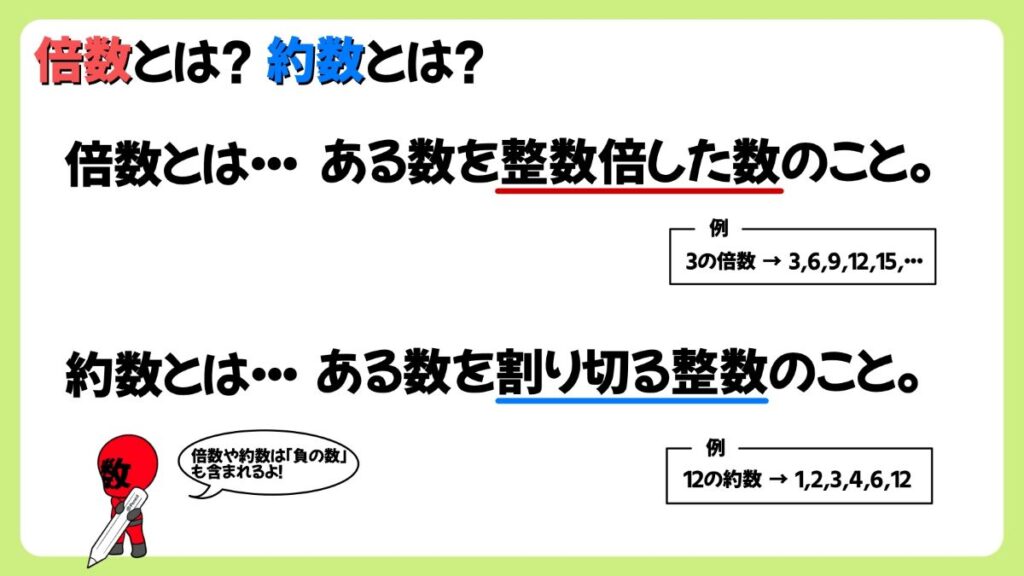
忘れている人も多いと思いますので、まずは倍数と約数について復習しておきましょう。
倍数とは
倍数とは”ある数を整数倍した数のこと”です。
例えば３の倍数であれば、３の段を言えばいいので、
- ３×１＝３
- ３×２＝６
- ３×３＝９
- ３×４＝１２
のようになり、３，６，９，１２，１５，・・・は３の倍数となります。
１２の倍数は、１２，２４，３６，４８，６０，・・・となり、お分かりのように、ある数の倍数は無限に存在します。
約数とは
約数とは”割り切る整数”のことです。
例えば１２の約数は、１，２，３，４，６，１２のことで、これらの数は１２を割り切ることができる整数です。
注意してほしいのは、倍数も約数も”整数”なので、中学校以降は負の数も含まれます。
例えば、ー１５は５の倍数ですし、４の約数は±１，±２，±４の６個となります。
今回は小学生向けなので、負の数は考えないものとするよ！
公倍数と公約数の意味
次に公倍数と公約数についての意味を理解しましょう。
公倍数の意味
公倍数とは”２つ以上の整数に共通する倍数のこと”です。
例
２の倍数は２，４，６，８，１０，１２，１４，１６，１８・・・
３の倍数は３，６，９，１２，１５，１８，２１，・・・
６，１２，１８，・・・が共通しているので、これらの数が２と３の公倍数となります。
公約数の意味
公約数とは”２つ以上の整数に共通する約数のこと”です。
例
１２の約数は１，２，３，４，６，１２
１６の約数は１，２，４，８，１６
１，２，４が共通しているので、これらの数が１２と１６の公約数となります。
最小公倍数とは
公倍数が分かれば、最小公倍数が何かも分かってきますよね？
最小公倍数とは”共通する倍数のうち、最も小さい数のこと”です。
２と３の最小公倍数は、公倍数の６，１２，１８，２４，３０，・・・のうち最小の数なので、６となるわけですね。
最小公倍数の求め方
前置きが大分長くなってしまいましたが、ここから最小公倍数を求める方法を解説します。
求め方①【倍数を書き出す】方法
小学校の教科書ではこの【倍数を書き出す方法】が紹介されています。
例 ９と１５の最小公倍数は？
まずは９と１５の倍数を書き出します。
９の倍数は９，１８，２７，３６，４５，５４，・・・
１５の倍数は１５，３０，４５，６０，７５・・・
最小の公倍数は４５なので、９と１５の最小公倍数は４５となります。
小学校の教科書に載っているような問題であれば、この解き方が分かっていれば、テストでも困ることはあまりないでしょう。暗算が得意な子は書き出さなくても、頭の中でできるようになればスピードも上がってくると思います。
しかし、いちいち書き出すと時間がかかることと、大きい数字には対応できないというデメリットがあります。
求め方②【連除法を使う】方法
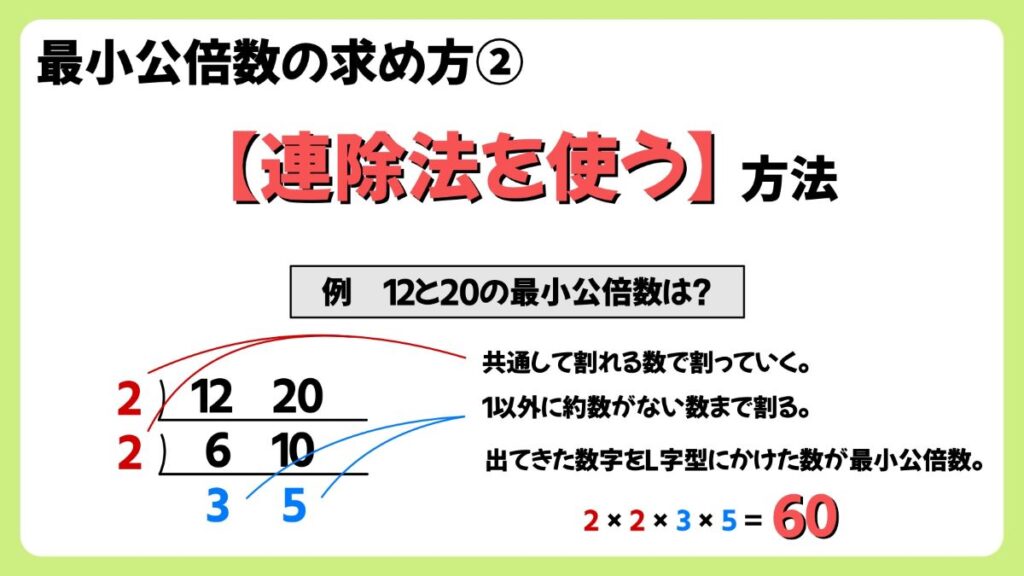
この【連除法を使う方法】であれば、【倍数を書き出す方法】のデメリットを補うことができます。
例 １２と２０の最小公倍数は？
１２と２０を割り算のひっさんの記号をひっくり返したものを書き、共通して割れる数で割っていきます。
１２と２０は共通して２で割れるので（４で割っても結果は同じ）、２で割るとそれぞれ６と１０なります。
６と１０はさらに２で割れるので、２で割ると、それぞれ３と５になります。
３と５は１以外約数を持たないので、ここで終わります。
出てきた数字、２、２、３、５をL字型にかけ算すると、２×２×３×５＝６０となり、１２と２０の最小公倍数は６０となります。
この連除法で求める方法をマスターすれば、大きな数字の最小故倍数でも求めることができます。
この連除法は、”はしご算”とも呼ばれているよ！
連除法（はしご算）を詳しく解説
上の説明で分かりづらいという人のために、画像で分かりやすく解説したものを載せておきます！
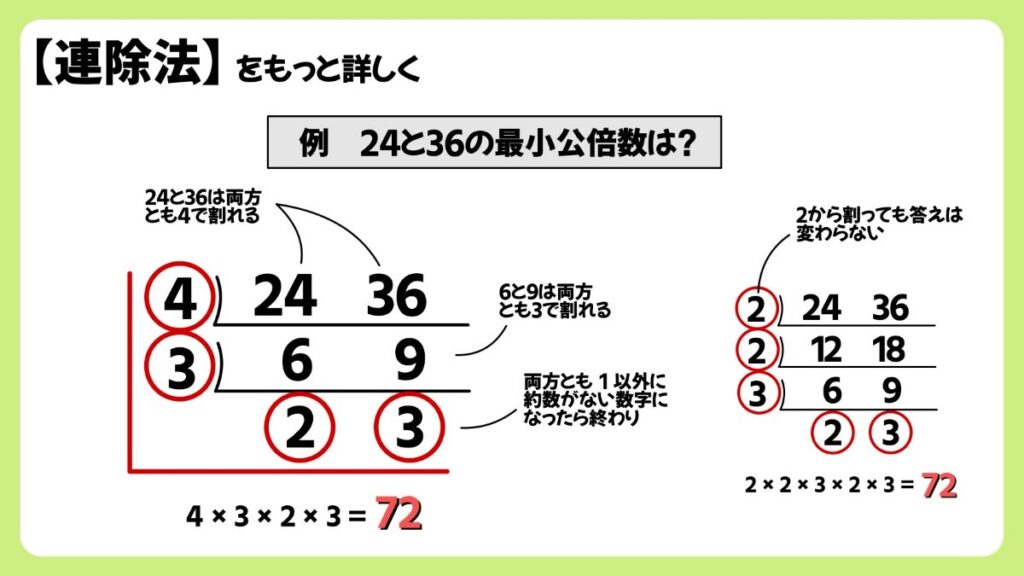
連除法の手順
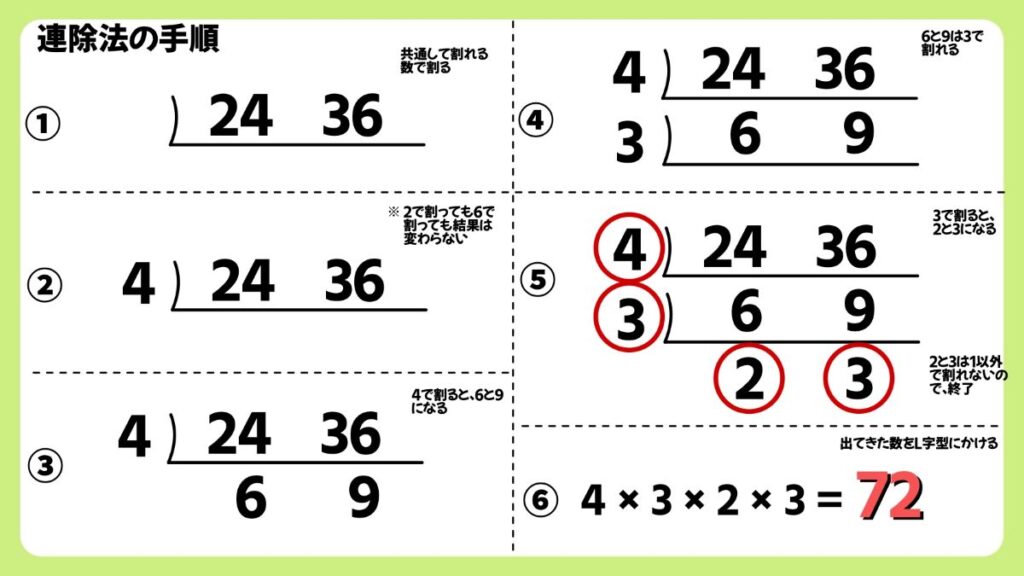
画像の解説では、最初に２で割っていますが、２４と３６は、最初に４、６で割ってもOKです。結果は変わりません。
最大公約数とは
次に最大公約数について解説をしていきます。
最大公約数とは”共通する約数のうち、最も大きい数のこと”です。
１２と１６の最大公約数は、公約数の１，２，４のうち、最小の数なので、４となるわけですね。
最大公約数の求め方
求め方①【約数を書き出す】方法
最小公倍数と同様、小学校の教科書ではこの【約数を書き出す方法】が紹介されています。
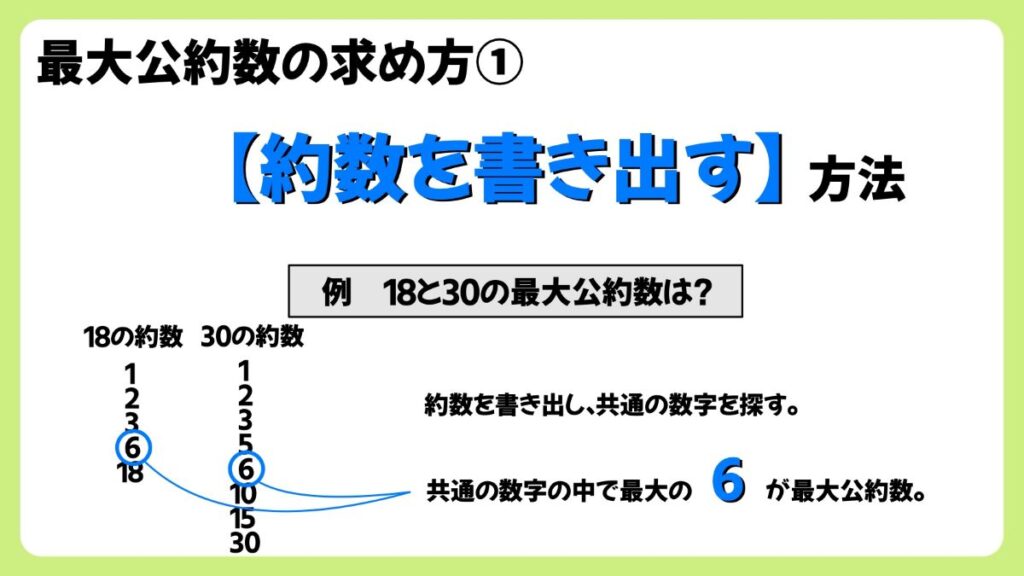
例 １８と３０の最大公約数は？
まずは１８と３０の約数を書き出します。
１８の約数は１，２，３，６，９，１８
３０の約数は１，２，３，５，６，１０，１５，３０
最大の公約数は６なので、１８と３０の最大公約数は６となります。
求め方②【連除法を使う】方法
やり方は最小公倍数のときと同じです。
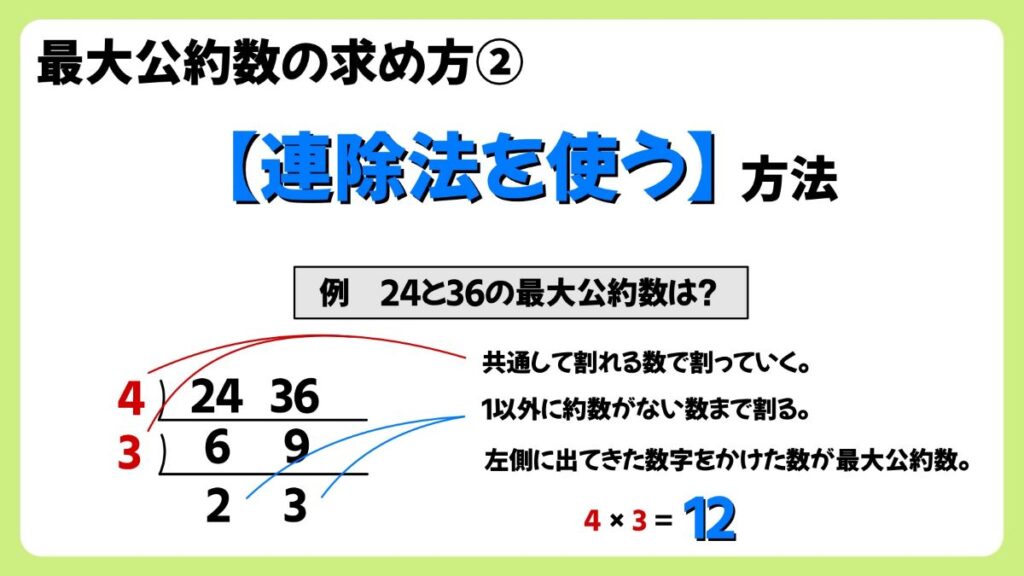
例 ２４と３６の最大公約数は？
２４と３６を割り算のひっさんの記号をひっくり返したものを書き、共通して割れる数で割っていきます。
２４と３６は共通して４で割れるので（２，６で割っても結果は同じ）、４で割るとそれぞれ６と９なります。
６と９は共通して３で割れるので、３で割ると、それぞ２と３になります。
２と３は１以外約数を持たないので、ここで終わります。
左側に出てきた数字、４、３をかけ算すると、４×３＝１２となり、２４と３６の最大公約数は１２となります。
最小公倍数のときは出てきた数字をL字型に全てかけ算しましたが、最大公約数の場合は左側に出てきた数字をかけ算することに注意しましょう。
※左側の数字だけかけ算するのは、左側に出てきた数字が共通因数だから。
まとめ
いかがだったでしょうか？まとめると、最小公倍数と最大公約数の解き方は２つです。
- 倍数（約数）を書き出す方法
- 連除法（はしご算）を使う方法
最小公倍数と最大公約数は一見難しく感じるかもしれませんが、ポイントを押さえればとてもシンプルです。
しかし、最小と最大が逆になってしまったりする間違いをする子供もとても多いので、言葉の意味から理解すると、しっかりとした定着が図れると思います！
投稿者プロフィール
-
現役で数学を教えている中学校の先生です。中学の数学のプリントやICT関連の情報、ブログでは道徳や学級レクのネタも発信しています。
このサイトはアフィリエイト広告（Amazonアソシエイト含む）を掲載しています。
最新の投稿
ブログ2025.02.13【足し算ピラミッド】大人も子供も楽しめる問題２０問！- ブログ2025.02.09【東大研パズル道場オンラインの口コミ】まとめ
- ブログ2025.02.05【最小公倍数と最大公約数の求め方】イラスト付きで分かりやすく解説！
- ブログ2025.01.26どの目が出るか分かる！？サイコロころころクイズ２０問！
