算数が好きになる話！小学生に聞かせたい数字の豆知識

　子どもが、算数が嫌いで困っている！どうしても算数に興味を持たせてあげられない！といった悩み、ありませんか？

　算数や数学は「考える力」を養う大切な学問の分野。もちろん受験でも避けては通れない教科なので、できるに越したことはありません。しかし、一度ついた苦手意識や、「算数は難しい」という先入観は、子どもの算数の力を伸ばすことを妨げてしまいます。

　今回の記事は、そんな子どもに、算数や数学に興味を持ってもらう小話や豆知識を紹介したいと思います。算数の授業の合間に、何気ない日常生活の中で子どもに話してあげれば、苦手意識を持つ子どもでも算数に興味を持つことができるでしょう！

RISU算数（タブレット学習教材）を数学教師がガチレビュー！

　数字はなぜできたの？

　大昔の人間は、数を人に伝えたり記録したりするとき、その数と同じ数の石を持ち歩いていました。しかし、その数が大きくなると石を持ち歩くのが面倒になったので、木の棒や動物の骨にきざみ目をつけて数を記録していました。それにも限界を感じたときに、数を表した便利な「数字」が開発されたと考えられています。石を持ち歩いたり、骨にきざみ目をつけたりする必要がなく、その文字を書けば、その数を伝えられるようになったのです。

　一番古いと言われている数字が、今から5000年以上前の古代エジプト王国の数字です。この国で使われていた数字は下の画像のような物の形をかたどったものでした。

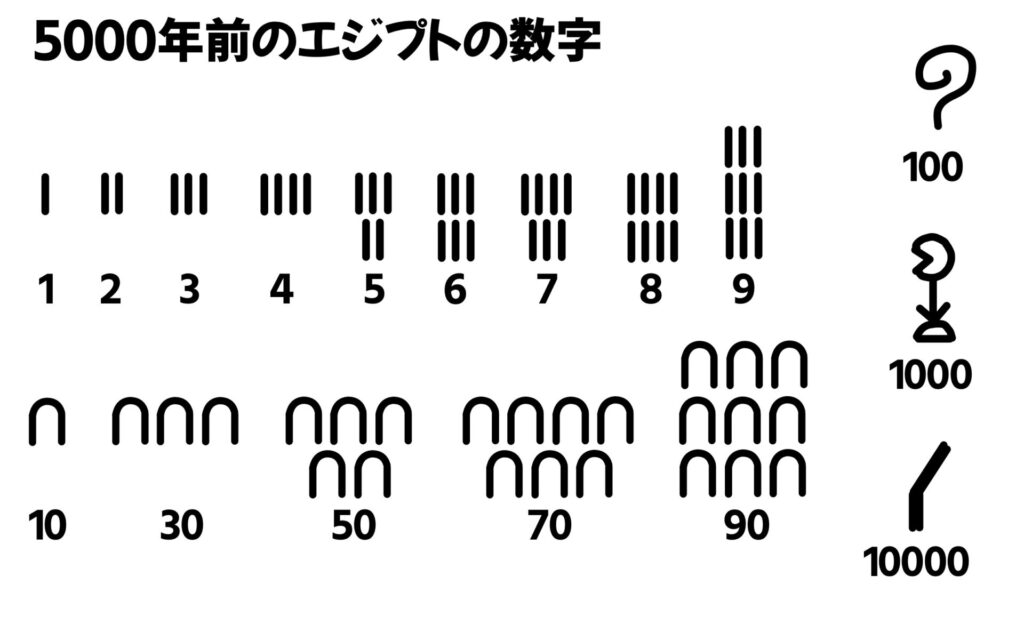
　1の位は「棒」の本数で、十くらいは「カゴの取っ手」を表したもの、百の位は物の長さを測るために使っていた「縄」、千の位は「蓮の花」、万の位は「葦」をモチーフにした記号です。

　計算で使う記号はなぜできたの？

　算数では、足し算は「＋」、引き算は「－」、かけ算は「×」、割り算は「÷」という記号を使います。これらは「演算記号」と呼ばれるのですが、これらの記号は500年ほど前のヨーロッパでつくられました。

　最初にできたのは「－」の記号です。これは船乗りがタルに入れておいた水を使ったとき、ここまで減った、という目印をに横線を使ったことが始まりとされています。次にできたのは「＋」の記号で、これはラテン語で「そして」を意味する「et」を雑に書いたことから「＋」という記号ができました。

　「×」はスコットランドの聖旗からきたという説や、十字架を斜めにしたという説があり、「÷」は分数の分母と分子の数を「・」で表したことが元になっていると考えられています。

　円周率には本当に終わりがない？

　大昔から円周率が「だいたい３」であることは知られていました。なぜならば、木を切った断面の直径の長さと円周の長さはほぼ３倍だったからです。しかし時代が進むにつれて、「だいたい３」では満足できなくなり、人々はもっと正確な値が知りたい！と思うようになりました。

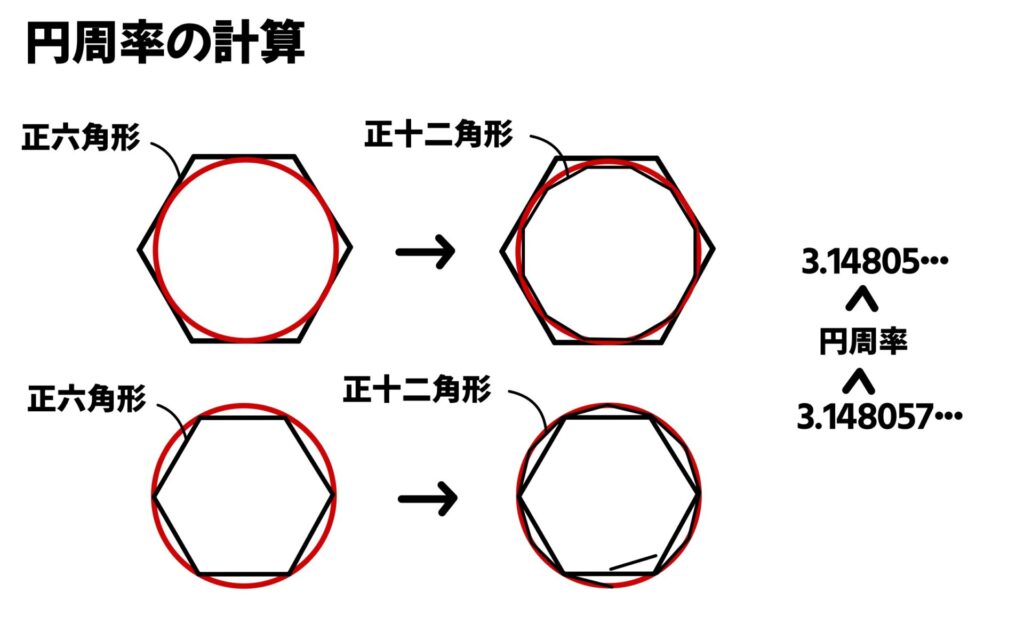
　直径１の円の中にちょうど角がおさまる正六角形をかき、その周りの長さを計算しました。次に正六角形を倍、倍、倍・・・としていき、最後は円に近い正九十六角形まで同じように周りの長さを計算しました。

　今度は円と正六角形を逆にして、正六角形にすっぽりおさまる円を書き、それを同じように倍にしていくと、円の外側でも正九十六角形まで計算しました。すると円周は円の内側の長さ3.14085より大きく、外側の3.142857より小さい数になることが分かりました。

　時代は流れ2022年6月にスーパーコンピューターを使った計算の結果、円周率は100兆まで算出したと言われています。

　なぜ１年は365日なの？

　1年が365日なのはみんな知っていることだけど、なんで365日なのか知っている人はあまりいませんよね。地球は太陽の周りをまわっていますが、太陽を１周するのにかかる時間がほぼ365日なのです。正確には「365日と6時間」ほどなのですが、何年間も365日で計算してしまうと、ズレが出てきてしまいますよね？その約６時間分のズレを4年に一度、修正する日を作りました。そう、それが4年に1度だけ1年が366日になる「うるう年」なわけです。

　ちなみに1日は地球が１回転する24時間、1か月は月の満ち欠けの新月から新月の間の約29.5日間となっています。

　マラソンはなぜ42.195㎞なの？

　約2500年前のギリシアのマラトンで、ギリシアとペルシアという国が戦争をしていました。この戦争はギリシア軍が勝利したのですが、一人のギリシア兵がマラトンからアテネまでの約42㎞を走り、戦争の勝利を伝えたのち、死んでしまいました。

　この話にちなんで、1896年にギリシアで開催された第1回のオリンピックでマラトンからアテネまでの競走が行われました。これがマラソンの始まりで、第4回のマラソンの距離が42.195㎞だったことから、その後のマラソンの距離は42.195㎞と決まったそうです。

　宝くじで１等が当たる確率はどれくらい低いの？

　ジャンボ宝くじの1等の当選金は約5億円で、その当選確率は約1000万分の１です。1000万分の１とは言っても、その確率はどれだけ低いのでしょうか？

　東京23区の人口が約1000万人なので、東京のすべての人が宝くじを1つずつ買って、その中の1人だけが当選するという確率になります。

　もっと身近なもので例えましょう。サイコロを用意してください。サイコロを振って1の目が出る確率は6分の１。2回連続で１が出る確率は6分の１×6分の１で、36分の１となります。それを繰り返していくと、9回連続で1が出る確率は約1000万分の１になります。つまり、サイコロを振って９回連続で１が出る確率と、宝くじの1等が当たる確率が同じくらいということになります。

　０（ゼロ）と０（レイ）の違い

　よく天気予報で、「降水確率０（レイ）パーセント」って言うけど、「０（ゼロ）パーセント」とは何が違うのか疑問に思ったことはないでしょうか。算数を勉強していて、０（レイ）とはあまり言わないですよね、実はそれには理由があるんです。

　０（ゼロ）は「全くない」という意味で、０（レイ）は「ほんの少しある」という意味で用いられます。つまり降水確率０（レイ）％とは、全く降らないわけではない、ということになります。

　０（ゼロ）という概念を生み出したのは古代インド人で、「無」という概念について思想を深めた結果０（ゼロ）の概念が生まれ、その後、世界中に伝わっていったとされています。０（レイ）は０（ゼロ）の概念が中国に伝わったのち、日本に入ってきたもので、「零」と書き、日本語となった漢語です。そのため０（ゼロ）と０（レイ）には若干のニュアンスの違いが生まれたようです。

　まとめ

　いかがだったでしょうか？子どもに聞かせたい算数が好きになる話を７個紹介しました。是非学校の生徒やお子様に話してみてください！